C++写矩阵的转置

　　(2019年2月19日注：这篇文章原先发在自己github那边的博客，时间是2017年2月5日)

　　对于任意非n阶矩阵的转置，用c++应该怎么写代码，思考了一下，发现并没有那么简单，上网找到了一个比较好的算法，叫做矩阵原地转置矩阵算法。基于别人的代码，改写成可以使用指针动态分配内存的方法。

　　先放传送门：C++实现矩阵原地转置算法的实现

　　原理并不难，那篇文章非常的详细，我不再赘述，下面把改写好的代码发出来。

/*************************************************************************
> File Name: matrix_transpose.cpp
> Author: SongLee
> Modified: JCChan
************************************************************************/
#include<iostream> 
using namespace std;
/* 后继 */
int getNext(int i, int m, int n)
{
    return (i%n)*m + i / n;
}
/* 前驱 */
int getPre(int i, int m, int n)
{
    return (i%m)*n + i / m;
}
/* 处理以下标i为起点的环 */
void movedata(int *mtx, int i, int m, int n)
{
    int temp = mtx[i]; // 暂存 
    int cur = i;    // 当前下标 
    int pre = getPre(cur, m, n);
    // 从最后一个数开始，获得它的前驱，直到前驱的值和最后一位值相等，相当于交换的逆过程
    while (pre != i)
    {
        mtx[cur] = mtx[pre];
        cur = pre;
        pre = getPre(cur, m, n);
    }
    mtx[cur] = temp;
}
/* 转置，即循环处理所有环 */
void transpose(int *mtx, int m, int n)
{
    for (int i = 0; i<m*n; ++i)
    {
        int next = getNext(i, m, n);
        while (next > i) // 若存在后继小于i说明重复 
            next = getNext(next, m, n);
        if (next == i)  // 处理当前环  
            movedata(mtx, i, m, n);
    }
}
void input(int *mtx, int row, int column) {
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < column; j++) {
            cout << "请输入矩阵的第" << i + 1 << "行第" << j + 1 << "个元素：";
            //    根据矩阵的坐标推算它在一维数组中的位置。
            cin >> *(mtx + column*i + j);
        }
    }
}
/* 输出矩阵 */
void print(int *mtx, int m, int n)
{
    for (int i = 0; i<m*n; ++i)
    {
        if ((i + 1) % n == 0)
            cout << mtx[i] << "
";
        else
            cout << mtx[i] << " ";
    }
}
/* 测试 */
int main()
{
    int row, column;
    cout << "请输入矩阵的行数：";
    cin >> row;
    cout << "请输入矩阵的列数：";
    cin >> column;
    int *matrix = new int[row*column];
    input(matrix, row, column);
    cout << "Before matrix transposition:" << endl;
    print(matrix, row, column);
    transpose(matrix, row, column);
    cout << "After matrix transposition:" << endl;
    print(matrix, column, row);
    delete[] matrix;
    system("pause");
    return 0;
}

　　结果如下

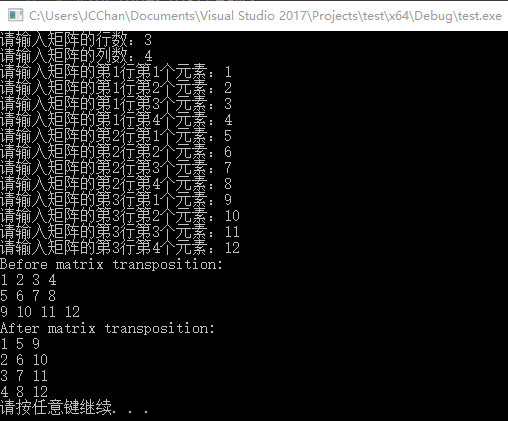
　　对于n阶方阵来说，情况则简单的多，同样放上代码。

#include<iostream>
using namespace std;
void move(int *matrix, int n)
{
    int i, j, k;
    for (i = 0; i<n; i++)
        for (j = 0; j<i; j++)
        {
            k = *(matrix + i*n + j);
            *(matrix + i*n + j) = *(matrix + j*n + i);
            *(matrix + j*n + i) = k;
        }
}
int main()
{
    int n, i, j;
    int *p;
    cout << "请输入矩阵的维数：";
    cin >> n;
    p = new int[n*n];
    cout << "输入矩阵的元素" << endl;
    for (i = 0; i<n; i++)
        for (j = 0; j<n; j++)
        {
            cout << "第" << i + 1 << "行第" << j + 1
                << "个元素为：";
            cin >> p[i*n + j];
        }
    cout << "输入的矩阵的为：" << endl;
    for (i = 0; i<n; i++)
    {
        for (j = 0; j<n; j++)
            cout << p[i*n + j] << " ";
        cout << endl;
    }
    move(p, n);
    cout << "转置后的矩阵的为：" << endl;
    for (i = 0; i<n; i++)
    {
        for (j = 0; j<n; j++)
            cout << p[i*n + j] << " ";
        cout << endl;
    }
    delete[] p;
    system("pause");
    return 0;
}