Codeforces Round #317 (Div. 2) D Minimization （贪心+dp）

D. Minimization

time limit per test 

2 seconds

memory limit per test 

256 megabytes

input 

standard input 

output 

standard output

You've got array A, consisting of n integers and a positive integer k. Array A is indexed by integers from 1 to n.

You need to permute the array elements so that value

became minimal possible. In particular, it is allowed not to change order of elements at all.

Input

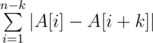
The first line contains two integers n, k (2 ≤ n ≤ 3·10⁵, 1 ≤ k ≤ min(5000, n - 1)).

The second line contains n integers A[1], A[2], ..., A[n] ( - 10⁹ ≤ A[i] ≤ 10⁹), separate by spaces — elements of the array A.

Output

Print the minimum possible value of the sum described in the statement.

You've got array A, consisting of n integers and a positive integer k. Array A is indexed by integers from 1 to n.

You need to permute the array elements so that value

became minimal possible. In particular, it is allowed not to change order of elements at all.

Input

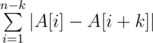
The first line contains two integers n, k (2 ≤ n ≤ 3·10⁵, 1 ≤ k ≤ min(5000, n - 1)).

The second line contains n integers A[1], A[2], ..., A[n] ( - 10⁹ ≤ A[i] ≤ 10⁹), separate by spaces — elements of the array A.

Output

Print the minimum possible value of the sum described in the statement.

按照下标取模后的值可以分成k组，对于一组来说，按照升序排相邻的差之和是最小的，可用交换法证明，不难看出，总和等于a[end]-a[start]。对于不同的两组，

公共元素一定在端点，同样交换法可证，因此将整个数组排序以后相同一组一定连续。有n%k个长度为n/k+1的，其他的长度为n/k。

因此需要决策长度的选法，定义dp[i][j]表示选了i个长度为n/k+1，j个长度为n/k的组的最小花费。那么决策是下一个区间是长或者是短，边界条件dp[0][0] = 0表示什么也不选的时候花费为0。dp[i][j] = min(dp[i-1][j]+cost(i-1,j,L),dp[i][j-1]+cost(i,j-1,S))。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e5+5, maxk = 5001;
int a[maxn];
int dp[2][maxk];
int n,k,len;

int cost(int i,int j,int L)
{
    int s = (i+j)*len+i, e = s+len+L-1;
    return a[e]-a[s];
}

int main()
{
    //freopen("in.txt","r",stdin);
    scanf("%d%d",&n,&k);
    for(int i = 0; i < n; i++) scanf("%d",a+i);
    sort(a,a+n);
    int tot = k, r = n%k;
    int L = r, S = tot-r;
    len = n/k;
    for(int i = 0; i <= L; i++){
        int cur = i&1, pre = cur^1;
        for(int j = 0; j <= S; j++){
            if(i && j) dp[cur][j] = min(dp[pre][j]+cost(i-1,j,1),dp[cur][j-1]+cost(i,j-1,0));
            else if(i) dp[cur][j] = dp[pre][j]+cost(i-1,j,1);
            else if(j) dp[cur][j] = dp[cur][j-1]+cost(i,j-1,0);
            else dp[cur][j] = 0;
        }
    }
    printf("%d",dp[L&1][S]);
    return 0;
}