希尔排序(Shell Sort)
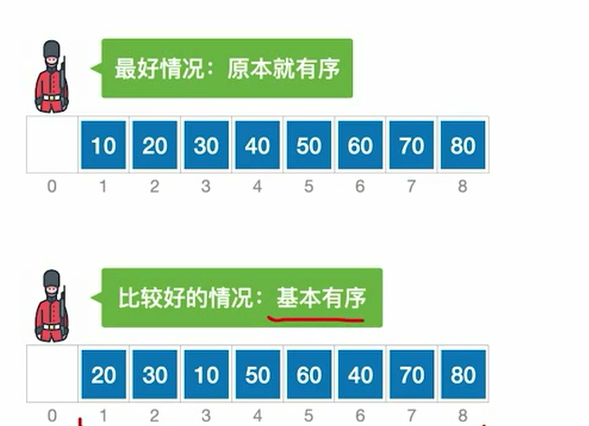
先追求表中的部分元素有序,再逐渐逼近全局有序
定义和操作步骤
先将待排序表分割成若干行形如L[i,i+d,i+2d,...,i+kd]的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止
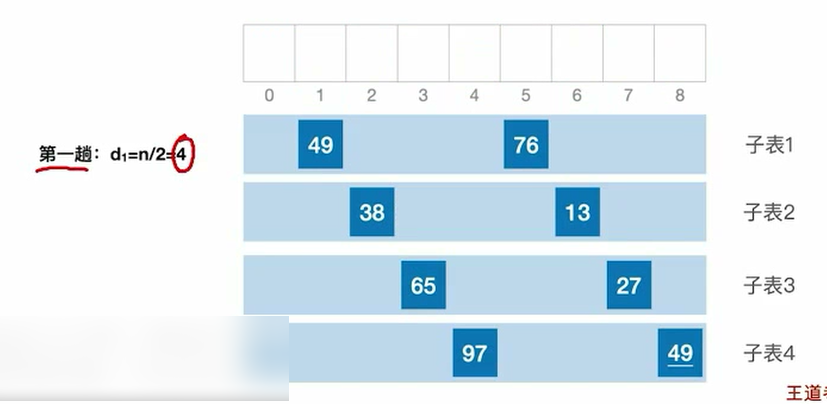
把相对的位置的大小顺序不对的对调。
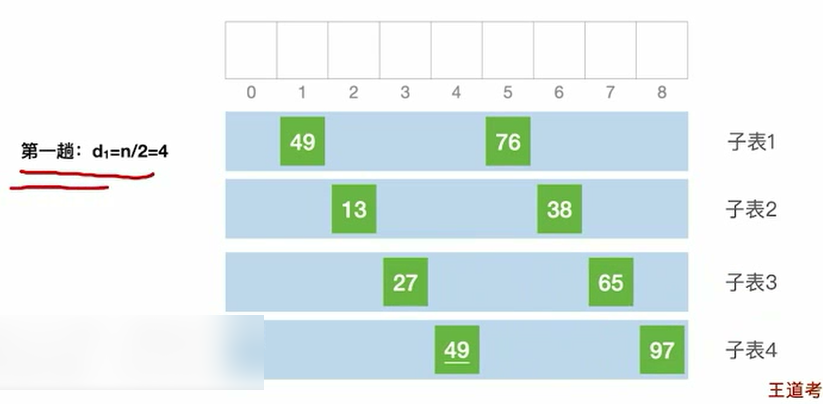
第二趟把增量d缩小,对每个子表进行直接插入排序
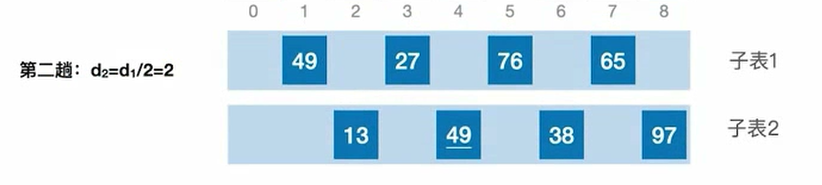
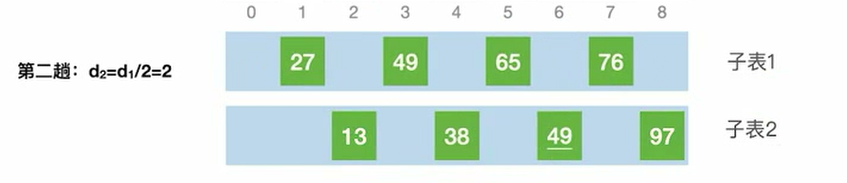
第三趟的时候,d已经变成1了,相当于对表进行操作。
整个表已呈现出“基本有序”,对整体在进行一次“直接插入排序”


考试中可能会遇到各种增量。判断当时序列的状态。
代码
//希尔排序
void ShellSort(int A[],int n){
int d,i,j;
//A[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已到
for(d=n/2;d>=1;d=d/2) //步长变化
for(i=d+1;i<=n;++i)
if(A[i]<A[i-d]){ //需将A[i]插入有序增量子表
A[0]=A[i]; //暂存在A[0]
for(j=i-d;j>0&&A[0]<A[j];j-=d)
A[j+d]=A[j];//记录后移,查找插入的位置
A[j+d]=A[0]; //插入
}
}
尝试实现直接处理完一个子表的
算法性能分析
空间复杂度:O(1)
时间复杂度:和增量序列d1,。。。的选择有关,目前无法用数学手段证明确切的时间复杂度
最坏时间复杂度为O(n2),当n在某个范围内时,可以达到O(n1.3)
稳定性:

不稳定。
适用性:仅适用于顺序表,不适用于链表
知识回顾