https://www.luogu.com.cn/problem/P2704
题目描述
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
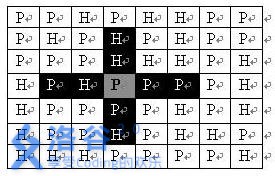
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。N≤100;M≤10。
输出格式
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
输入输出样例
输入 #1
5 4 PHPP PPHH PPPP PHPP PHHP
输出 #1
6
判断此行是否合法需要枚举上一行和上两行的状态,直接枚举所有状态是肯定会超时的,这时候我们就需要通过题目要求减少状态量了。
(dp要开三维:第一维表示行数,第二维表示现在枚举的状态,第三维表示上一行的状态,所以dp[i][j][k]表示第i行状态为第j个可行状态,且上一行状态是第k个可行状态的最大数量)
总结一下此类题目的dp方法:若某个状态可以对下n行的状态造成影响,那么就要预处理前n行合法的,对于n + 1行及以后,判断某状态是否合法需要往上枚举n行,所以dp数组要开n + 1维,第一维表示行数,第二维表示现在的状态,再往后第n维表示上n - 2行的状态(其实不可能出太多行的,时间指数增长)
这样dp就这样进行:
for(所有状态) for(所有状态) ...{向上枚举n行} dp[i][j][k][l]...[n + 1] += dp[i - 1][k][l]...[最上面一行]; //求最大方案数就max() //意会吧,不怎么讲得清楚
代码:
1 #include <bits/stdc++.h> 2 typedef long long LL; 3 const int INF=0x3f3f3f3f; 4 const double eps =1e-8; 5 const int mod=1e8; 6 const int maxn=1e5+10; 7 using namespace std; 8 9 LL dp[105][1050][1050];//dp[i][j][k]表示第i行状态为第j个可行状态,且上一行状态是第k个可行状态的最大数量 10 int line[105];//第i行的状态,相当于把第i行中的0,1拼接在一起 11 int state[1050];//第i个可行状态是多少 12 int need[1050];//第i个可行状态中1的个数 13 int can[105][1050];//第i行中第j个可行方案是否可行 14 int cnt; 15 16 int main() 17 { 18 #ifdef DEBUG 19 freopen("sample.txt","r",stdin); 20 #endif 21 22 int n,m; 23 scanf("%d %d",&n,&m); 24 for(int i=1;i<=n;i++) 25 { 26 char str[15]; scanf("%s",str); 27 for(int j=0;j<m;j++) 28 line[i]=(line[i]<<1) + (str[j]=='P'); 29 } 30 for(int i=0;i<(1<<m);i++) 31 { 32 if(((i<<1)&i)==0 && ((i<<2)&i)==0) 33 { 34 state[++cnt]=i; 35 //need[cnt] = __builtin_popcount(i);用这个可省略下面的 36 int t=i; 37 while(t) 38 { 39 need[cnt] += t%2; 40 t>>=1; 41 } 42 } 43 } 44 for(int i=1;i<=cnt;i++)//第一行 45 { 46 if((state[i]|line[1])==line[1]) 47 { 48 can[1][i]=1; 49 dp[1][i][0]=need[i]; 50 } 51 } 52 for(int i=1;i<=cnt;i++)//第二行 53 { 54 if((state[i]|line[2])==line[2]) 55 { 56 can[2][i]=1; 57 for(int j=1;j<=cnt;j++) 58 { 59 if(!can[1][j]) continue; 60 if((state[i]&state[j])==0) 61 { 62 dp[2][i][j]=max(dp[2][i][j],dp[1][j][0]+need[i]); 63 } 64 } 65 } 66 } 67 for(int i=3;i<=n;i++) //处理剩下的,所以从 3 开始枚举 68 { 69 for(int j=1;j<=cnt;j++) //枚举该行状态 70 { 71 if((state[j]|line[i])==line[i]) 72 { 73 can[i][j]=1; 74 for(int k=1;k<=cnt;k++) //枚举上一行状态 75 { 76 if(!can[i-1][k]) continue; 77 if(state[j]&state[k]) continue; //上下不能相邻 78 for(int g=1;g<=cnt;g++) //枚举上两行状态 79 { 80 if(!can[i-2][g]) continue; 81 if((state[j]&state[g])||(state[k]&state[g])) continue; 82 dp[i][j][k]=max(dp[i][j][k], dp[i-1][k][g]+need[j]); 83 } 84 85 } 86 } 87 88 } 89 } 90 LL ans=0; 91 for(int i=1;i<=cnt;i++) 92 { 93 for(int j=1;j<=cnt;j++) 94 ans=max(ans, dp[n][i][j]); 95 } 96 printf("%lld ",ans); 97 98 return 0; 99 }
这个和上面的稍微有点不同,省去了can数组(可忽略)
1 #include <bits/stdc++.h> 2 typedef long long LL; 3 const int INF=0x3f3f3f3f; 4 const double eps =1e-8; 5 const int mod=1e8; 6 const int maxn=1e5+10; 7 using namespace std; 8 9 LL dp[105][1050][1050];//dp[i][j][k]表示第i行状态为第j个可行状态,且上一行状态是第k个可行状态的最大数量 10 int line[105];//第i行的状态,相当于把第i行中的0,1拼接在一起 11 int state[1050];//第i个可行状态是多少 12 int need[1050];//第i个可行状态中1的个数 13 int cnt; 14 15 int main() 16 { 17 #ifdef DEBUG 18 freopen("sample.txt","r",stdin); 19 #endif 20 21 int n,m; 22 scanf("%d %d",&n,&m); 23 for(int i=1;i<=n;i++) 24 { 25 char str[15]; scanf("%s",str); 26 for(int j=0;j<m;j++) 27 line[i]=(line[i]<<1) + (str[j]=='P'); 28 } 29 for(int i=0;i<(1<<m);i++) 30 { 31 if(((i<<1)&i)==0 && ((i<<2)&i)==0) 32 { 33 state[++cnt]=i; 34 need[cnt] = __builtin_popcount(i); 35 } 36 } 37 for(int i=1;i<=cnt;i++)//第一行 38 { 39 if((state[i]|line[1])==line[1]) 40 dp[1][i][0]=need[i]; 41 } 42 for(int i=1;i<=cnt;i++)//第二行 43 { 44 if((state[i]|line[2])==line[2]) 45 { 46 for(int j=1;j<=cnt;j++) 47 { 48 if((state[j]|line[1])!=line[1]) continue; 49 if((state[i]&state[j])==0) 50 { 51 dp[2][i][j]=max(dp[2][i][j],dp[1][j][0]+need[i]); 52 } 53 } 54 } 55 } 56 for(int i=3;i<=n;i++) //处理剩下的,所以从 3 开始枚举 57 { 58 for(int j=1;j<=cnt;j++) //枚举该行状态 59 { 60 if((state[j]|line[i])==line[i]) 61 { 62 for(int k=1;k<=cnt;k++) //枚举上一行状态 63 { 64 if((state[k]|line[i-1])!=line[i-1]) continue; 65 if(state[j]&state[k]) continue; //上下不能相邻 66 for(int g=1;g<=cnt;g++) //枚举上两行状态 67 { 68 if((state[g]|line[i-2])!=line[i-2]) continue; 69 if((state[j]&state[g])||(state[k]&state[g])) continue; 70 dp[i][j][k]=max(dp[i][j][k], dp[i-1][k][g]+need[j]); 71 } 72 73 } 74 } 75 76 } 77 } 78 LL ans=0; 79 for(int i=1;i<=cnt;i++) 80 { 81 for(int j=1;j<=cnt;j++) 82 ans=max(ans, dp[n][i][j]); 83 } 84 printf("%lld ",ans); 85 86 return 0; 87 }
-