分类模型的F1分值、Precision和Recall 计算过程
引入
通常,我们在评价classifier的性能时使用的是accuracy
考虑在多类分类的背景下
accuracy = (分类正确的样本个数) / (分类的所有样本个数)
这样做其实看上去也挺不错的,不过可能会出现一个很严重的问题:例如某一个不透明的袋子里面装了1000台手机,其中有600台iphone6, 300台galaxy s6, 50台华为mate7,50台mx4(当然,这些信息分类器是不知道的。。。)。如果分类器只是简单的把所有的手机都预测为iphone6, 那么通过上面的公式计算的准确率accuracy为0.6,看起来还不错;可是三星,华为和小米的全部预测错了。如果再给一个袋子,里面装着600台galaxy s6, 300台mx4, 50台华为mate7,50台iphone,那这个分类器立马就爆炸了,连回家带孩子的要求都达不到
所以,仅仅用accuracy来衡量一个分类器的性能是很不科学的。因此要引入其他的衡量标准。
二分类
是不是经常看见如下类似的图?这是二分类的图,假设只有正类和负类,True和False分别表示对和错;Positive和Negative分别表示预测为正类和负类。

那么
- TP:预测为Positive并且对了(样本为正类且预测为正类)
- TN:预测为Negative并且对了(样本为负类且预测为负类)
- FP:预测为Positive但错了(样本为负类但预测为正类)
- FN:预测为Negative但错了(样本为正类但预测为负类)
- TP+FP:预测为Positive并且对了+预测为Positive但错了=预测为Positive的样本总数
- TP+FN:预测为Positive并且对了+预测为Negative但错了=实际为Positive的样本总数
所以precision就表示:被正确预测的Positive样本 / 被预测为Positive的样本总数
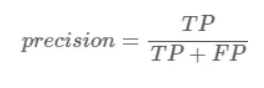
同理,recall就表示:被正确预测的Positive样本 / 实际为Positive的样本总数
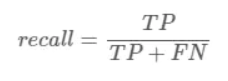
F1是调和平均值,精准率和召回率只要有一个比较小的话,F1的值也会被拉下来:

多分类情况
其实和二分类情况很类似,例子如下 这个是Micro , 和二分类类似 (将例子中的precision和recall代入到F1公式中,得到的就是Micro下的F1值)

而Macro情况下计算F1需要先计算出每个类别的F1值,然后求平均值。如下

Macro情况下上述例子的计算

sklearn计算程序(macro)
下面是使用sklearn直接计算多类别F1/P/R的程序,将接口中的average参数配置为’macro’即可。
from sklearn.metrics import f1_score, precision_score, recall_score
y_true=[1,2,3]
y_pred=[1,1,3]
f1 = f1_score( y_true, y_pred, average='macro' )
p = precision_score(y_true, y_pred, average='macro')
r = recall_score(y_true, y_pred, average='macro')
print(f1, p, r)
# output: 0.555555555556 0.5 0.666666666667
参考链接: