python 金融应用（一）期权定价公式的计算

一.基于不付息的欧式期权看涨BSM公式

假定股票服从下列微分方程：

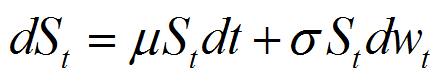
期权定价公式：

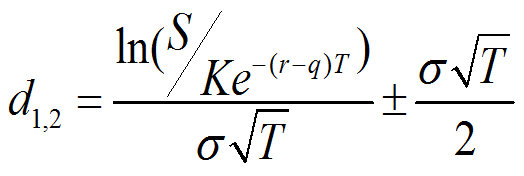
二.蒙特卡洛模拟

import numpy as np
import math
from time import time

np.random.seed(20000)


t0=time()

s0=100.0;K=105.0;T=1.0;r=0.05;sigma=0.2
m=50;dt=T/m;I=250

S=np.zeros((m+1,I))   
S[0]=s0
for t in range(1,m+1):
    z=np.random.standard_normal(I)
    S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+ sigma *math.sqrt(dt)*z)

c0=np.exp(-r*T)*np.sum( np.maximum(S[-1]-K,0))/I

tnp1=time()-t0

print(c0,tnp1)

7.124219040864565 0.0