坐标转换

管线在处理顶点数据时需要经过多个坐标系的转换。
1.通过model与view矩阵先将其变换到世界坐标系中,再将其变换到观察坐标系中。从而方便后续处理。
2.经透射投影,将3D坐标映射到视平面,完成从3D到2D的变换,从而在后续可转换为在屏幕显示的2D坐标。
3.透射投影将顶点转换到了单位立方体中,变换到标准化设备坐标系。
4.而标准化设备坐标系中的物体常常会产生形变,为恢复物体原比例,将其进行视口变换,转换到最后显示的屏幕坐标系中。
以上为顶点在坐标转换中的大致流程,其中包含的很多细节部分会在下面结合透射投影进行详细分析。
逻辑分析
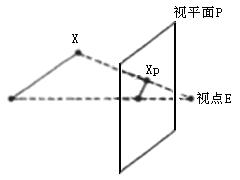
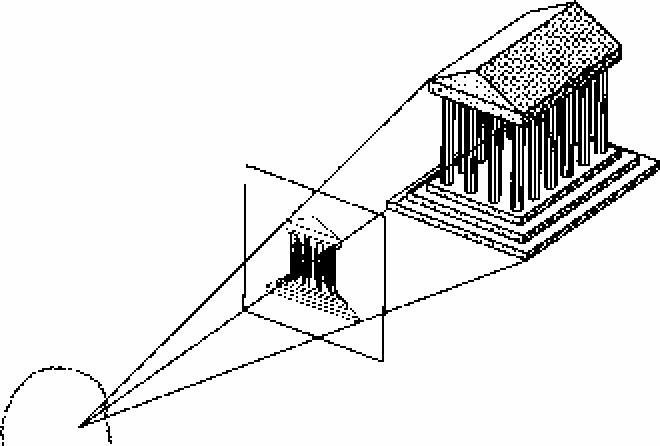
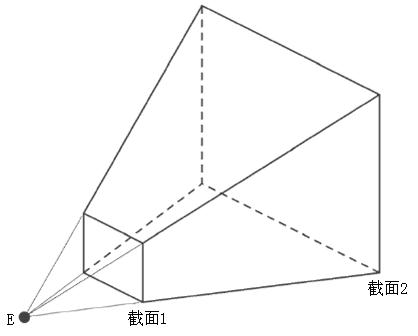
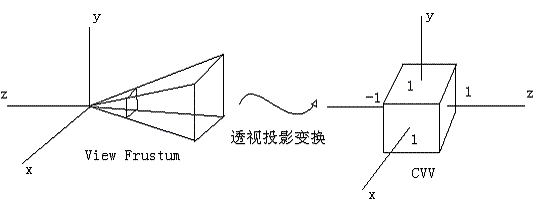
图 1 图 2 图 3 图4
1.转换:我们输入在程序中的坐标都是3D,而最终显示在屏幕上的只能是2D。所以可想而知,需要一个过程来将3D坐标映射到我们的2D视平面上。只有这样我们才能通过显示器去观看。
2.观察:如上述图1,我们在观察面上所观察到的正是观察点E与物体实际坐标的连线在视平面P上的交点,其比例也可形成近大远小的现实感。图2可直观的感受。
3.问题:根据学过的知识,显然这一交点可以很轻松的通过相似三角形来求得。但问题是,我们需要获得多大范围内的物体?即限定观察空间。不在观察空间内的物体又该怎样去处理?即裁剪。
4.观察空间:设定近平面,远平面,和观察角度,来得到一个视椎体(frustum)。而我们也常常将近平面作为视平面。如图3。
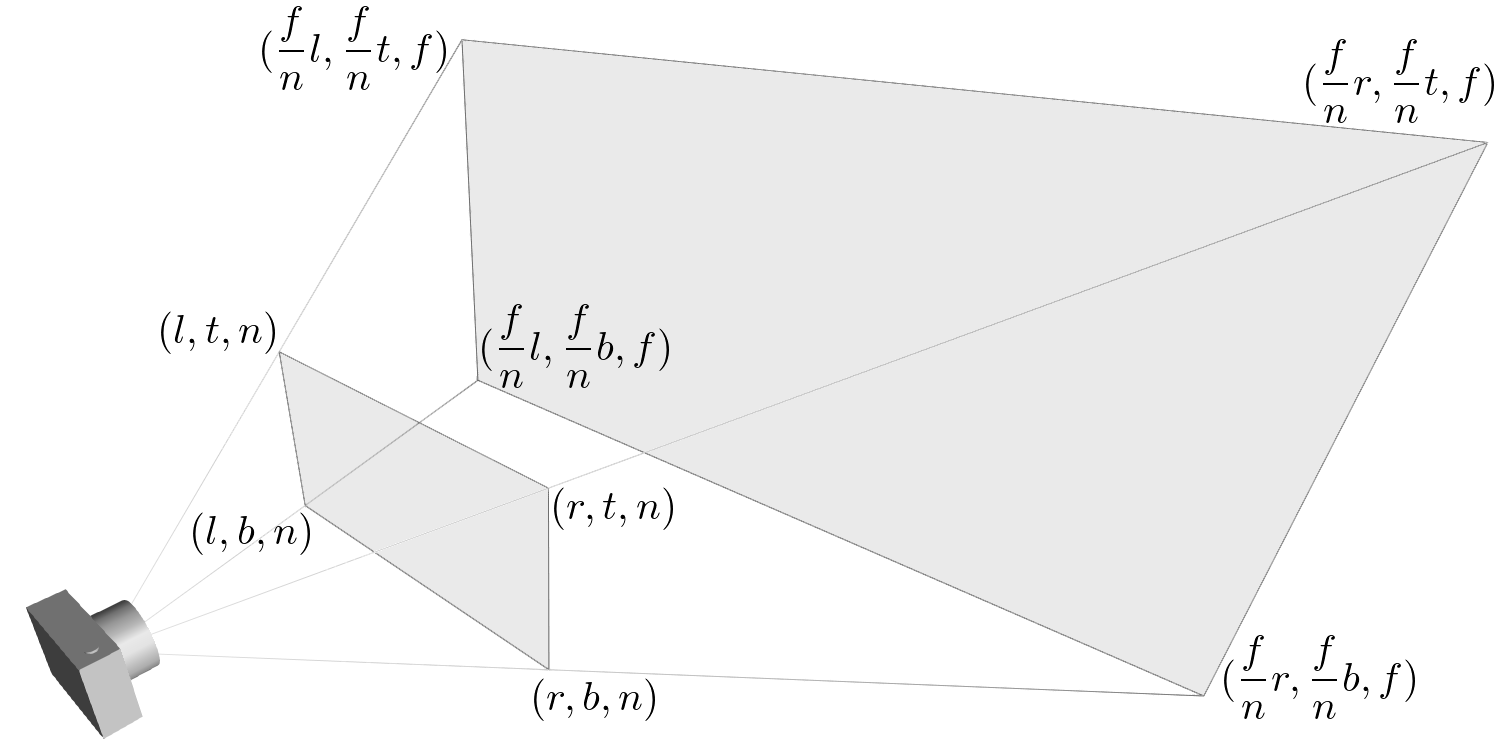
5.裁剪:裁剪掉视锥体以外的顶点,只保留以内的。若直接对视锥体裁剪,因平面的倾斜也会导致计算量过大,所以采用将其映射到单位立方体中(CVV),此时都为垂直平面,并且在映射过程中,顶点与视锥体的关系不变,在视锥体外的仍然在视锥体外。裁剪时只需判定一个坐标即可,大大减少了计算量。如图4。
6.恢复:但是在映射到CVV的时候,顶点间的比例产生了变化,物体常常产生形变,所以在映射到屏幕坐标系时,必须对其进行比例恢复。采用的方法是:将近平面(即视平面)的宽高比例一开始就调整为与视口宽高比相同。所以在恢复比例时,只需要再与比例进行乘除等操作即可。(视口并非电脑屏幕大小,视口指的是我们要渲染的尺寸。视口是<=电脑屏幕大小的,我们通常在程序中将视口与窗口大小保持一致,所以视口也表现为程序运行后的窗口尺寸。)
数学推导(2种表达式)
透视投影的过程分为4部分进行。
1、将视锥体中的顶点投影到视平面
2、将视锥体映射到CVV(规则观察体)中进行裁剪
3、进行透视除法。
4、进行视口变换,恢复其比例,最终将其映射到屏幕坐标系中。
公式推导1(线性插值法)
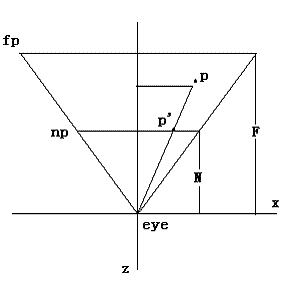
参数介绍:np:近截面 fp:远截面 p':投影后的顶点 p:物体顶点 N:近截面到观察点的距离 F: eye:观察点 (取近截面为投影面)
根据p与p'的相似三角形性质可得:
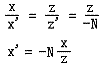
同理,在z轴和y轴上可得:
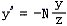
从而得到投影后得坐标:
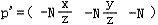
到此,已把顶点投影到视平面,此时所有点的z值均为-N。若以此为最终坐标,则无法在后续中进行深度测试等操作,所以需要保留原本顶点在空间中的z值。
由此可把坐标最终定为:
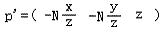
此坐标的x与y是相对于视平面的,而z是相对于原先的空间坐标。可以想象若用此坐标来构成原物体,则已经产生形变。
在逻辑分析中已解释了在CVV中裁剪的原因,接下来就是把视锥体映射到CVV中,即把视锥体内的物体都变换到CVV中。
1. 涉及到变换,则需要构造出一个变换矩阵,从而用此矩阵来完成映射。而矩阵中的各种变换就要求我们把顶点坐标转换为齐次坐标。
2.被忽视的重要环节:任何顶点最终显示在屏幕上,都要经过插值和光栅化的过程,然后再渲染光栅化得到的片段,最终显示在屏幕的像素中。而透视投影的插值也是使用线性插值,但是x',y'与z并非线性关系,经过推导可得出x',y'与1/z是成线性关系的。若能把p'中的z变换为带有1/z的形式,则会更加方便后期操作。
3.由于要把p'转换为齐次坐标,而齐次坐标在变换为普通坐标时,需要同除w,x'和y'中均为x和y同除以了-z。所以也需要把p'中的z变换为带有-1/z的形式,从而更方便齐次坐标到普通坐标的转换。
4.要把z方向上的值都映射到CVV中,即区间 [-1,1]。可以选取合适的系数,当z=-N时,取-1。当z=-F时,取1。
综上多点,我们对p'的z进行形式转化,最终得到:
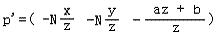
对于这种形式,就可以很轻松的进行矩阵和齐次变换了
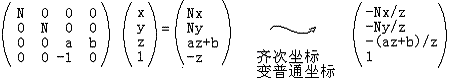
其中
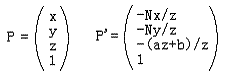
先在z轴上进行从视锥体到CVV的映射
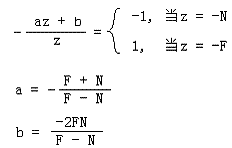
再对x轴和y轴进行映射(此时是把投影后的x'和y'坐标,映射到CVV中)
我们知道-Nx / z的有效范围是投影平面的左边界值(left)和右边界值(right),即区间[left, right],而y的边界值-Ny / z则映射到区间[bottom, top]。而现在我们想把-Nx / z属于[left, right]映射到-Nx / z属于[-1, 1]中,-Ny / z属于[bottom, top]映射到-Ny / z属于[-1, 1]中。采用的方法是线性插值。

综上可得p'的坐标为:
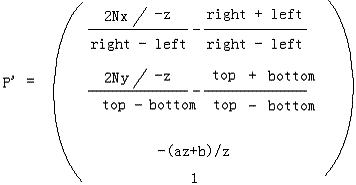
这个坐标是齐次坐标经透视除法后得到的,我们做透视除法的逆操作,同乘1/w得:
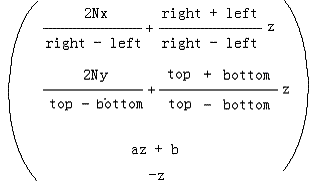
变换为矩阵形式:
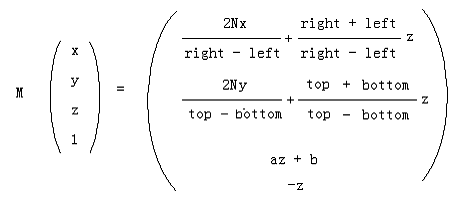
从而求得我们想要得最终变换矩阵M表达式:
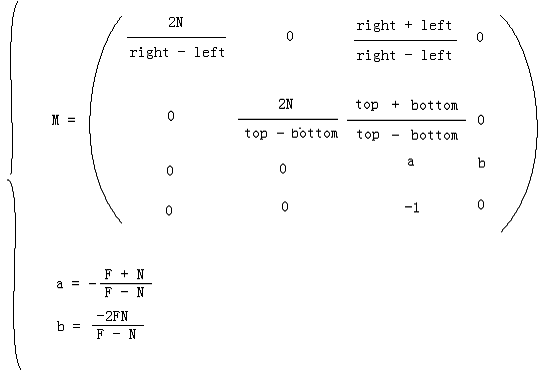
以上就是透视投影矩阵的数学推导过程。但是到此仍然有很多问题,因为只知道公式是无法具体结合应用的,而且在很多程序中给出的都是类似于aspect的公式,好像并没有用到上述推导的公式。还有上述的left和right边界在视口和屏幕坐标系中又是何种意义?在以下,我将进行说明。
公式推导2(等比变换法)
在程序种,我们很少用到以上形式,因为参数过多,较为复杂,更为普遍的是以下形式。2种形式的区别在于,对x和y进行映射时采用的方法不同。
公式1采用线性插值,公式2采用等比的方式。
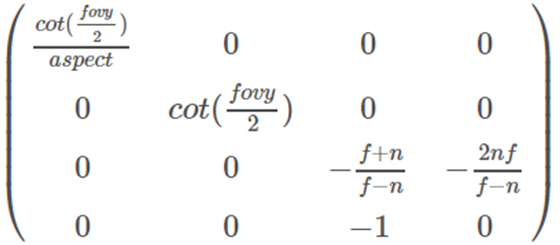
Z方向的推导过程不变,最终得到的仍为:
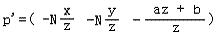
由于此时,x'=-Nx/z与y‘=-Ny/z均在视平面上,只需要将视平面变换到CVV的单位截面即可。设最终变换到CVV中的坐标为x'' , y'',投影平面高为H。因为CVV长宽高均为2
则由等比变换可得:y'/y''= H/2
解得:y''=-(y/z)*cot(fovy/2)
同理可得:x''=-(x/z)*cot(fovy/2)*(1/aspect)
求矩阵时对其做齐次坐标逆处理,同乘-z。从而综上可得矩阵M为
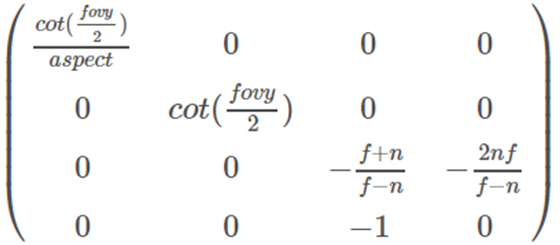
对比2种推导过程,公式1采用线性插值更复杂,所以常用的是公式2中的等比变换。得到的矩阵也更为简单。所以在程序中若打开底层矩阵的定义,我们可发现采用的均为公式2。
参数说明
一、投影平面的上下左右边界与代码的关系。
1.在正常的程序中用到的代码为 glm::perspective( glm::radians(fov) , (float)SCR_WIDTH / (float)SCR_HEIGHT , 0.1f , 100.0f ) ;以此构造出透视投影矩阵,第一个参数为fov,即y方向上视野角度的大小。第二个参数为我们设定运行后窗口的宽高比(即aspect)。第三、四个分别为近截面和远截面距观察点的距离。
2.令fovy=radians(fov) 。则tan(fovy/2)=height/0.1f,从而可求出height。再由height乘上aspect可得出width。从而确定了视锥体前后上下左右6个面的坐标。由此就可求出之前推导出的矩阵M中的所有参数了。
3.直接看glm::perspective的参数,会产生迷惑,因为这个函数隐藏了利用fov和aspect求各个面的过程。

由此图也可看出,函数中另有一个函数glFrustum。
二、投影平面的边界与管线流程的关系
1.因为我们通常将视口渲染尺寸设为窗口尺寸,所以以上所有推导的过程中都包含着视口尺寸=窗口尺寸的隐藏条件。
2.在 glm::perspective( glm::radians(fov) , (float)SCR_WIDTH / (float)SCR_HEIGHT , 0.1f , 100.0f ) 中,把投影面的宽高比设定成了和视口宽高比相同。这是因为在讲投影面上的图形映射到CVV中时,CVV的宽高比为1,这就导致图形产生失真现象。解决这一问题,就是在视口变换中按照投影面原先设定的比例变换到视口中,又因为原先设定的比例就与视口相同,所以最终渲染出的比例当然也就是恢复原样了。而视口尺寸比例又与窗口尺寸比例相同,则最终在窗口中看到的图形为正常投影后的保真图形。