Knight Moves
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 26102 | Accepted: 12305 |
Description
Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
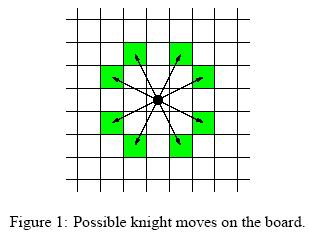
For people not familiar with chess, the possible knight moves are shown in Figure 1.
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
For people not familiar with chess, the possible knight moves are shown in Figure 1.

Input
The input begins with the number n of scenarios on a single line by itself.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
Output
For
each scenario of the input you have to calculate the minimal amount of
knight moves which are necessary to move from the starting point to the
ending point. If starting point and ending point are equal,distance is
zero. The distance must be written on a single line.
Sample Input
3 8 0 0 7 0 100 0 0 30 50 10 1 1 1 1
Sample Output
5 28 0
下棋,从一个坐标到另一个坐标最少几步,
第一个输入T个样例
第一行一个数L表示棋盘大小
然后两行两个坐标
1 #include<stdio.h> 2 #include<queue> 3 #include<string.h> 4 using namespace std; 5 int p[333][333]; 6 int main() 7 { 8 int T; 9 scanf("%d", &T); 10 while (T--) 11 { 12 memset(p, -1, sizeof(p)); 13 queue<int>q; 14 int L; 15 scanf("%d", &L); 16 int a, b, x, y; 17 scanf("%d%d%d%d", &a, &b, &x, &y); 18 p[a][b] = 0; 19 q.push(a * 1000 + b);//一个坐标转为一个数——前三位是横坐标后三位是纵坐标 20 while (!q.empty()) 21 { 22 int t = q.front(); 23 q.pop(); 24 a = t / 1000; 25 b = t % 1000; 26 if (a == x&&b == y) 27 { 28 printf("%d ", p[a][b]); 29 break; 30 } 31 if (a - 1 >= 0 && b + 2 < L&&p[a - 1][b + 2] == -1) 32 { 33 q.push((a - 1) * 1000 + (b + 2)); 34 p[a - 1][b + 2] = p[a][b] + 1; 35 }// 36 if (a + 1 < L && b + 2 < L&&p[a + 1][b + 2] == -1) 37 { 38 q.push((a + 1) * 1000 + (b + 2)); 39 p[a + 1][b + 2] = p[a][b] + 1; 40 }// 41 if (a - 2 >= 0 && b + 1 < L&&p[a - 2][b + 1] == -1) 42 { 43 q.push((a - 2) * 1000 + (b + 1)); 44 p[a - 2][b + 1] = p[a][b] + 1; 45 }// 46 if (a - 2 >= 0 && b - 1 >=0&&p[a - 2][b - 1] == -1) 47 { 48 q.push((a - 2) * 1000 + (b - 1)); 49 p[a - 2][b - 1] = p[a][b] + 1; 50 }// 51 if (a + 2 <L && b + 1 < L&&p[a + 2][b + 1] == -1) 52 { 53 q.push((a + 2) * 1000 + (b + 1)); 54 p[a + 2][b + 1] = p[a][b] + 1; 55 }// 56 if (a + 2<L && b - 1 >=0&&p[a + 2][b - 1] == -1) 57 { 58 q.push((a + 2) * 1000 + (b - 1)); 59 p[a + 2][b - 1] = p[a][b] + 1; 60 }// 61 if (a - 1 >= 0 && b - 2 >=0&&p[a - 1][b - 2] == -1) 62 { 63 q.push((a - 1) * 1000 + (b - 2)); 64 p[a - 1][b - 2] = p[a][b] + 1; 65 }// 66 if (a + 1<L && b - 2>=0&&p[a + 1][b - 2] == -1) 67 { 68 q.push((a + 1) * 1000 + (b - 2)); 69 p[a + 1][b - 2] = p[a][b] + 1; 70 }//八个可能的位置 71 } 72 } 73 }