链接
https://www.acwing.com/problem/content/description/1136/
题目
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1 到 N。
问从顶点 1 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 2 个正整数 N,M,为图的顶点数与边数。
接下来 M 行,每行两个正整数 x,y,表示有一条顶点 x 连向顶点 y 的边,请注意可能有自环与重边。
输出格式
输出 N 行,每行一个非负整数,第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出对 (100003) 取模后的结果即可。
如果无法到达顶点 i 则输出 0。
数据范围
(1≤N≤10^5,)
(1≤M≤2×10^5)
输入样例:
5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
输出样例:
1
1
1
2
4
思路
先抛开这道题想一下最短路计数问题如何解决:
引入一个概念——“最短路树”:
假设每个点的父亲节点是这个点任意一条最短路径的前节点,那么就会形成一颗树,同时也会有其他条最短路的前节点,总之也会满足拓扑序。
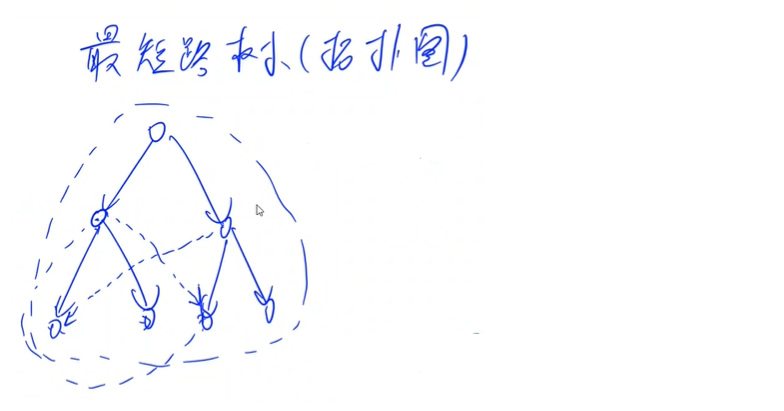
求解最短路算法有:
bfs:只适用于边权为0和1的图,对于每个点更新最短路时可以直接更新最短路数量,因为每个点只会入队和出队一次,bfs的过程满足拓扑序。
Dijkstra:也在每个点更新最短路时可以直接更新最短路数量,因为每个点只会作为距离最近的节点出队一次。
spfa:不能直接计算最短路数量,因为每个节点都有可能多次入队和出队,spfa本质是对于以边相同的点为同一层优先搜索的,举个例子:

假设spfa先搜完1->2->3->4,3和4的最短路都确定,最短路条数都为1,再搜到1->6->7->8->3这条路时,只会将3的最短路计数加1,4的最短路还是1。
那么就会有人提出,当最短路数量更新时也加入队列,那么如果将3加入队列,对于4,不能确定最短路条数时加1还是加2。
但是这并不代表spfa不能求最短路条数。当边权有负时,只能用spfa计数,一种有效的做法是:先用spfa将每个点的单源最短路求出,枚举每条边,当有(d[v[i]]=w[i]+d[u[i]])时,建一条边u到v的边,最后做拓扑DP,记录每个点可以被走到的方案数。(写这么多其实也是向讲一下spfa的做法,但是现在还没找到有这样的题,如果有机会给学弟们出题自己可以出一道)
对于这道题边权为1的图,可以直接用bfs,也可以用spfa(边权为1的spfa对于每个距离相同点可以保证同时搜到)。对于每个点v,u可以更新v的最短距离,那么v的计数等于u的计数;如果u的更新等于d[v],那么v的计数加上u的计数。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=100010,M=400010,mod=100003;
int h[N],nex[M],e[M],idx;
int d[N],q[N],st[N],cnt[N],n,m;
void add(int u,int v){
nex[idx]=h[u];
e[idx]=v;
h[u]=idx++;
}
void bfs(){
memset(d,0x3f,sizeof d);
d[1]=0;
cnt[1]=1;
int hh=0,tt=0;
q[tt++]=1;
st[1]=1;
while(hh!=tt){
int u=q[hh++];
if(hh==N) hh=0;
st[u]=0;
for(int i=h[u];~i;i=nex[i]){
int v=e[i];
if(d[v]>d[u]+1){
d[v]=(d[u]+1)%mod;
cnt[v]=cnt[u];
if(!st[v]) {
q[tt++]=v;
if(tt==N) tt=1;
st[v]=1;
}
}
else if(d[v]==d[u]+1){
(cnt[v]+=cnt[u])%=mod;
if(!st[v]) {
q[tt++]=v;
if(tt==N) tt=1;
st[v]=1;
}
}
}
}
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=1;i<=m;++i){
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
bfs();
for(int i=1;i<=n;++i){
cout<<cnt[i]<<endl;
}
return 0;
}