二分法查找

# 二分查找(折半查找)

title: 二分查找
tags: 数据结构与算法之美
author: 辰砂

---

一、简介

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列 （解释：所以二分查找的时候一定要是有序的数组）

二、过程

若k==R[mid].key，查找成功
若k<R[mid].key，则high=mid-1
若k>R[mid].key，则low=mid+1

1.查找 21

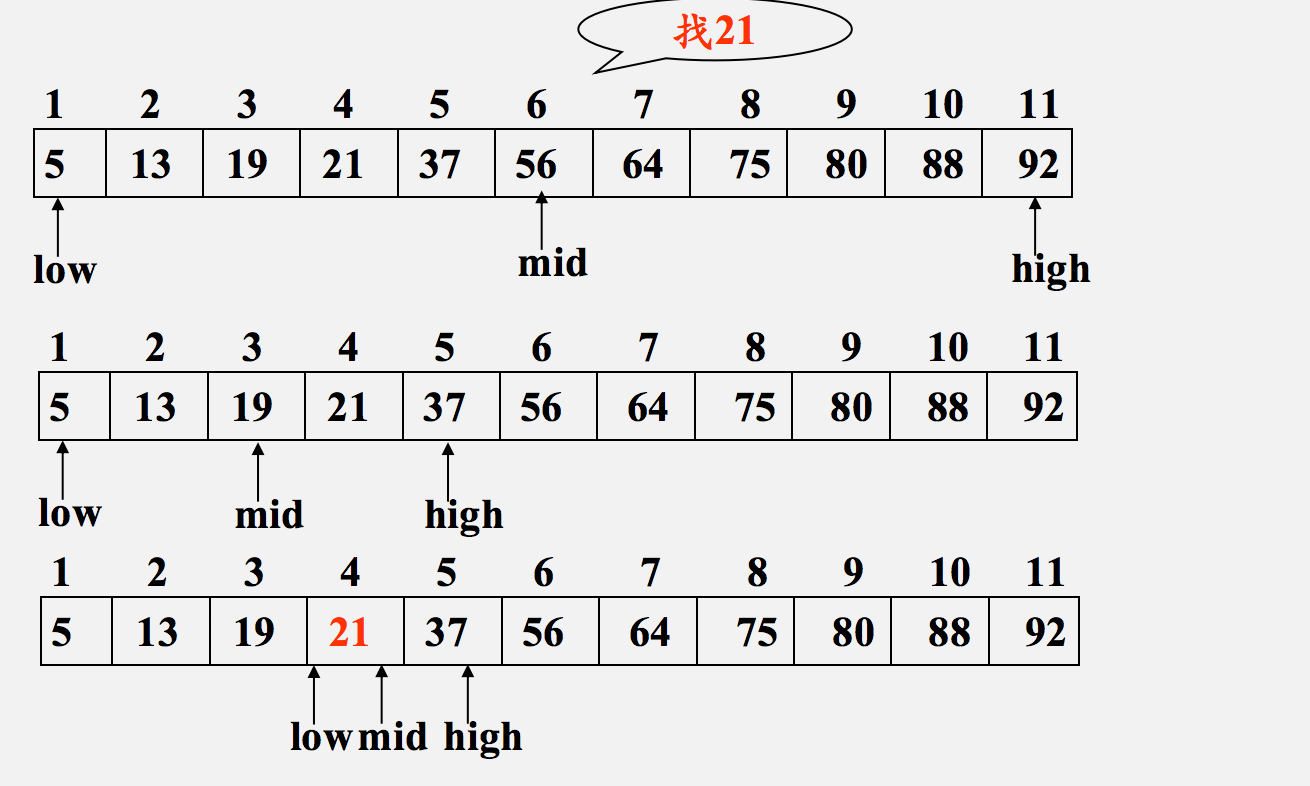
2.查找70

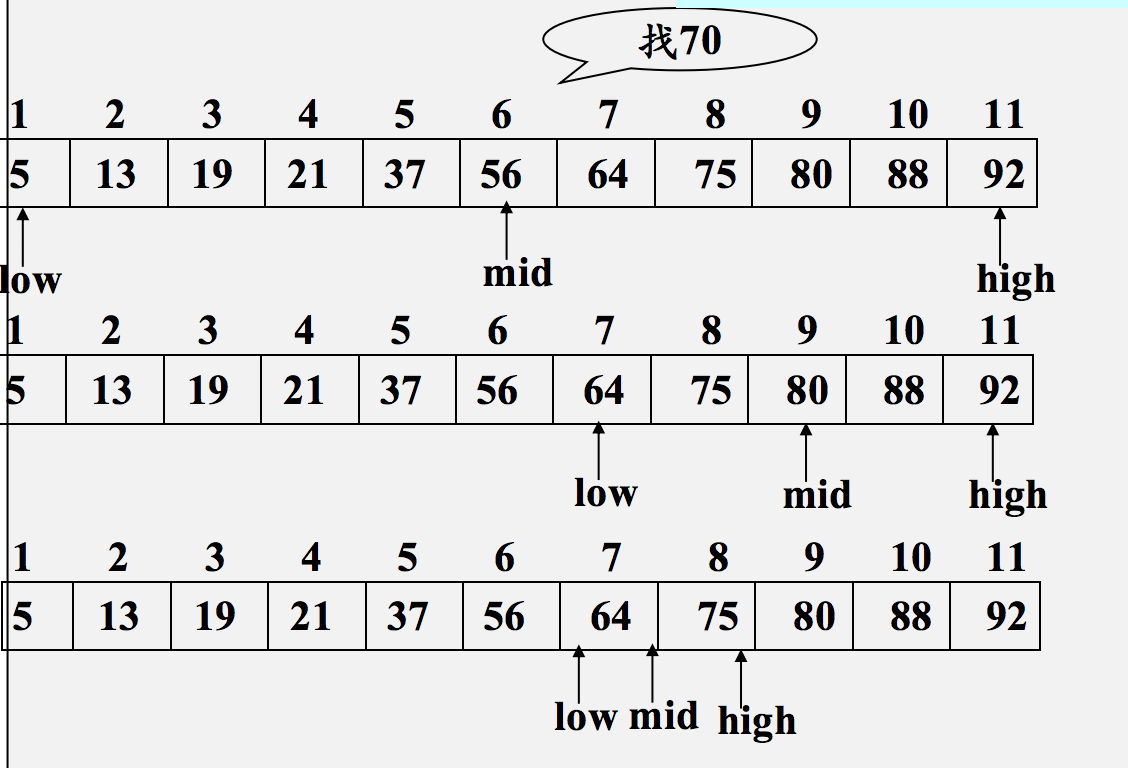
三、算法描述

1.非递归

设表长为n，low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值

初始时，令low=1,high=n,mid=(low+high)/2

让k与mid指向的记录比较

若k==R[mid].key，查找成功

若k<R[mid].key，则high=mid-1

若k>R[mid].key，则low=mid+1

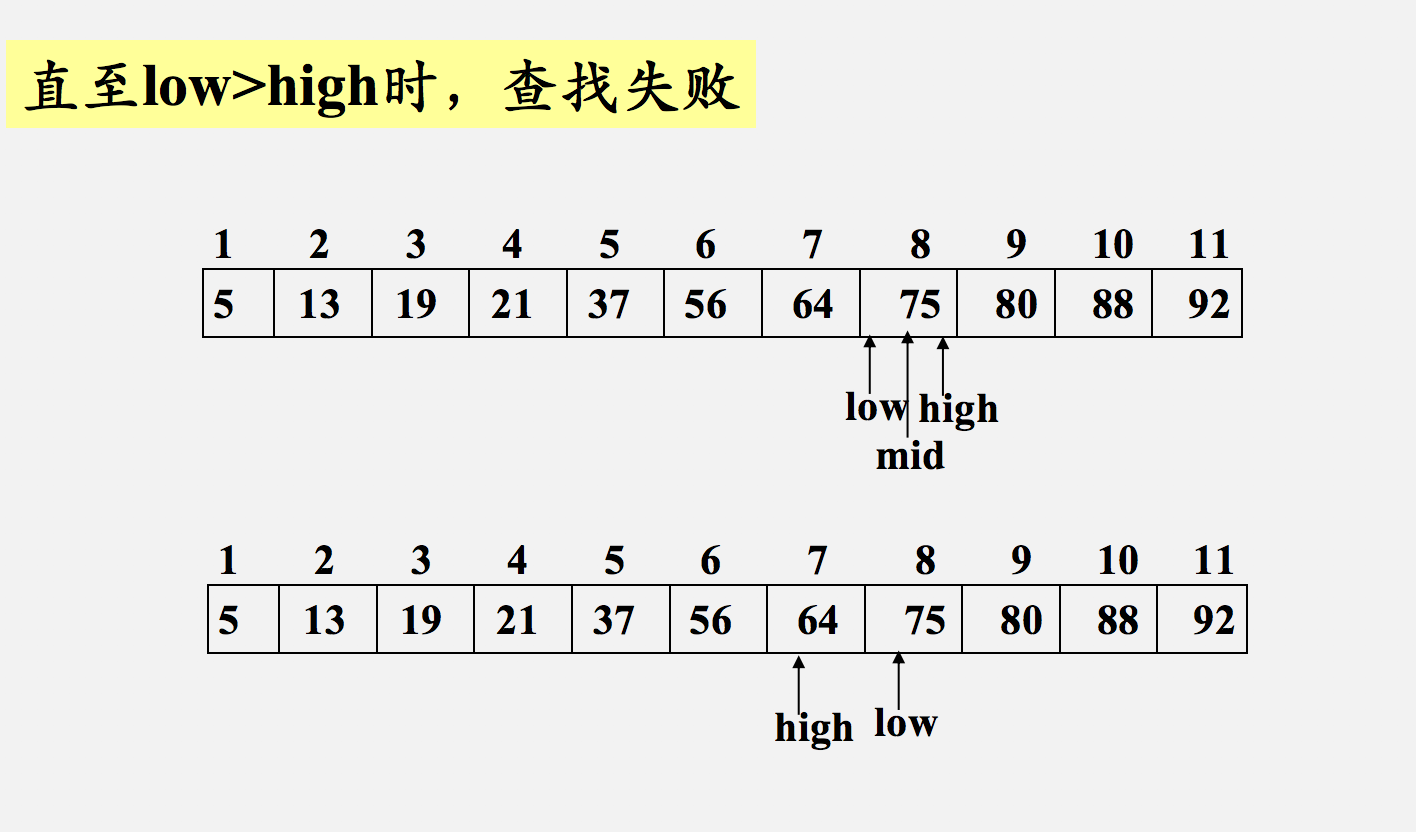
重复上述操作，直至low>high时，查找失败

int Search_Bin(SSTable ST,KeyType key){
//若找到，则函数值为该元素在表中的位置，否则为0
    low=1;high=ST.length;
　　while(low<=high){
        mid=(low+high)/2;
        if(key==ST.R[mid].key) return mid; 
        else if(key<ST.R[mid].key) high=mid-1;//前一子表查找
        else low=mid+1;                             //后一子表查找
    }                                       return 0;       //表中不存在待查元素
}

2.递归

int Search_Bin (SSTable ST, keyType key, int low, int high) 
{ 
  if(low>high) return 0;   //查找不到时返回0 
  mid=(low+high)/2; 
  if(key==ST.elem[mid].key)  return mid; 
  else if(key<ST.elem[mid].key)  
    return search_Bin(ST,key,low,mid-1);//递归
  else  return search_Bin(ST,key,mid+1,high); //递归
} 

3、完整代码

public class BinarySearch {

    public static void main(String[] args) {

        int[] nums = {1, 4, 5, 8, 9};
        System.out.println(binarySearch(nums, 1));
        System.out.println(binarySearchRecursion(nums, 1, 0, nums.length - 1));
    }

    /**
     * 循环
     *
     * @param nums
     * @param target
     *
     * @return
     */
    public static int binarySearch(int[] nums, int target) {
        if (nums.length < 0) {
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = (left - right) / 2 + right;
            if (target == nums[mid]) {
                return mid;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;
    }

    /**
     * 递归
     *
     * @param nums
     * @param target
     * @param left
     * @param right
     *
     * @return
     */
    public static int binarySearchRecursion(int[] nums, int target, int left, int right) {

        if (nums.length < 0 || left < 0 || right > nums.length - 1) {
            return -1;
        }

        int mid = (left - right) / 2 + right;
        if (left <= right) {
            if (target == nums[mid]) {
                return mid;
            } else if (target > nums[mid]) {
                return binarySearchRecursion(nums, target, mid + 1, right);
            } else {
                return binarySearchRecursion(nums, target, left, mid - 1);
            }
        }
        return -1;
    }

四、折半查找的性能分析

判定树：树中每个结点表示表中一个记录，结点中的值为该记录在表中的位置，通常称这个查找过程的二叉树称为判定树。折半查找法在成功时进行比较的关键字个数最多不超过树的深度。（折半查找的运行过程可以用二叉树来描述，这棵树通常称为“判定树”）

关键字的平均比较次数，也称平均搜索长度ASL(Average Search Length)

如上图而言是11个节点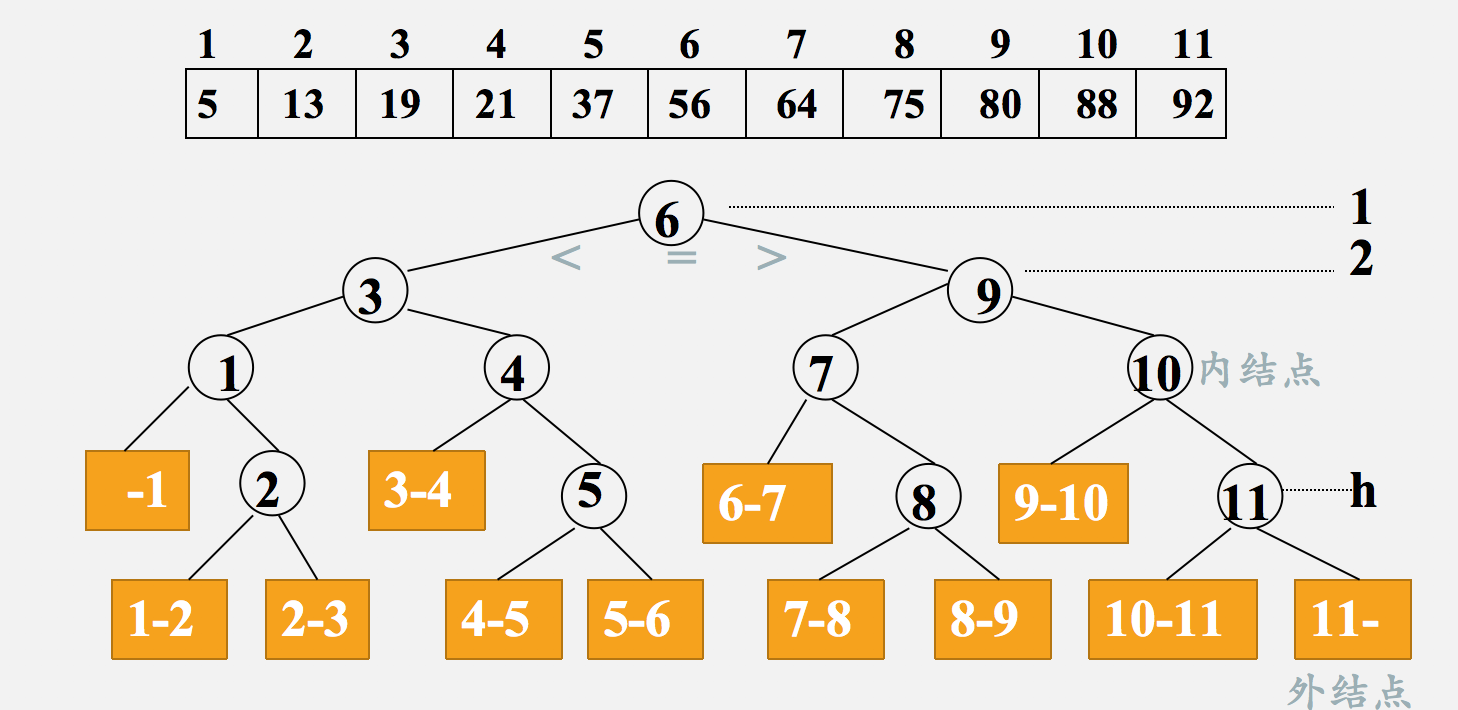

假设概率都相等的情况下：ASL＝1/11(11＋2×2＋4×3+4*4 )＝33/11=3
查找成功时比较次数：为该结点在判定树上的层次数，不超过树的深度 d =  log2 n  + 1
查找不成功的过程就是走了一条从根结点到外部结点的路径d或d-1。

查找过程：每次将待查记录所在区间缩小一半，比顺序查找效率高,时间复杂度O(log2 n)

适用条件：采用顺序存储结构的有序表，不宜用于链式结构

五、优化

由上面可以知道二分法的代码的核心

mid=(low+high)/2;
if(key==ST.R[mid].key) return mid; 
 else if(key<ST.R[mid].key) high=mid-1;//前一子表查找
  else low=mid+1;

思考：极端情况下会不会产生数组溢出，答案是肯定的，因为极端情况下，当high为int类型的临界最大值的时候，low只要变化，两者相加肯定会溢出。为了效率更高，我们也可以用位运算，

改进代码：

int mid = (left - right) >> 2 + right;

六、二分法练习

https://leetcode.com/problemset/all/?topicSlugs=binary-search

---

参考

https://www.cnblogs.com/ciyeer/p/9065781.html