[整理]CSPS 2021 瞎胡

考场上没仔细看 T3，结果出来发现是傻逼题，亏大了属于是。

T1

估计难度：提高-。
国内和国际分开处理，考虑预处理出分配不同廊桥个数时停靠的飞机数。
然后发现随着廊桥个数增长，飞机数是不降的，而且已经占有廊桥的飞机占有的廊桥一定不会改变，所以我们就删掉已经停下的飞机，每次扫一遍，二分找到下一个能够停靠的飞机。容易发现由于每架飞机最多只会停下一次，所以是均摊 \(O(n\log n)\) 的。
考场代码（那个链表好像没用了来着，考场上懒得删了）：

const int N=100010;
int n,m1,m2;
struct Node {
  int l,r;
  bool operator < (const Node &rhs)const{
    return l<rhs.l;
  }
}a[2][N];
struct Chain {
  int pre[N],nxt[N];set<pii > lps;//left pos
  void Del(int o,int x){
    pre[nxt[x]]=pre[x],nxt[pre[x]]=nxt[x];
    lps.erase(mkp(a[o][x].l,x));
  }
  void Init(int o,int lmt){
    for(int i=1;i<=lmt;i++)pre[i]=i-1,nxt[i]=i+1;
    for(int i=1;i<=lmt;i++)lps.insert(mkp(a[o][i].l,i));
    nxt[0]=1,nxt[lmt]=0;
  }
  int Calc(int o){
    int res=0,lst=0;
    for(int i=nxt[0];i;){
      res++,Del(o,i),lst=i;
      auto it=lps.lower_bound(mkp(a[o][i].r,i));
      if(it==lps.end())break;
      i=(*it).y;
    }
    return res;
  }
}l1,l2;
int ans1[N],ans2[N],ans;
int main(){
  Read(n),Read(m1),Read(m2);
  for(int i=1;i<=m1;i++)Read(a[0][i].l),Read(a[0][i].r);
  for(int i=1;i<=m2;i++)Read(a[1][i].l),Read(a[1][i].r);
  sort(a[0]+1,a[0]+1+m1),sort(a[1]+1,a[1]+1+m2);
  l1.Init(0,m1),l2.Init(1,m2);
  for(int x=1;x<=n;x++){
    ans1[x]=ans1[x-1]+l1.Calc(0);
    ans2[x]=ans2[x-1]+l2.Calc(1);
  }
  for(int i=0;i<=n;i++){
    ans=max(ans,ans1[i]+ans2[n-i]);
  }
  printf("%d\n",ans);
  KafuuChino HotoKokoa
}

题外话：不太懂为啥会有人三分……希望大家面对小样例上成立的性质一定要小心谨慎……

T2

估计难度：提高。
是一道简单的区间 dp，重点在于想到如何不重不漏地枚举和写出式子后的优化。
我们发现直接设状态不行，因为形如 \(\texttt{ASBSC}\) 的状态会重复枚举。不难想到原因是我们转移 \(\texttt{ASB}\) 型时没有规定 \(\texttt{A}\) 和 \(\texttt{B}\) 的样子，所以只需要强行让一边是左右匹配的即可。
这时发现 \(\texttt{ASB}\) 的一次转移还是 \(O(n^2)\) 的，考虑如何优化。
容易发现枚举中间的星号段时左右端点显然都是递增的，所以可以类似双指针的方式维护一段的和来转移。
代码（\(f\) 表示当前区间最左和最右的括号不配对，\(g\) 表示必须配对）：

const int N=510,p=1e9+7;
int n,K;char s[N];
int f[N][N],g[N][N];
bool sb[N][N];//subete *
int nxt[N];
int main(){
  Read(n),Read(K),scanf("%s",s+1);
  for(int i=1;i<=n;i++){
    sb[i][i-1]=1;
    for(int j=i;j<=n;j++){
      if(s[j]=='*'||s[j]=='?')sb[i][j]=1;
      else break;
    }
  }
  for(int i=1;i<n;i++){
    if(s[i]=='*'||s[i+1]=='*')continue;
    if(s[i]!=')'&&s[i+1]!='(')g[i][i+1]=1;//()
  }
  for(int l=3;l<=n;l++){
    for(int i=1;i+l-1<=n;i++){
      int j=i+l-1;
      if(s[i]=='*'||s[j]=='*')continue;
      if(s[i]==')'||s[j]=='(')continue;
      if(j-i-1<=K&&sb[i+1][j-1])g[i][j]=1;//(S)
      (g[i][j]+=(f[i+1][j-1]+g[i+1][j-1])%p)%=p;//(A)
      for(int k=2;k<=K+1&&i+k<j-1;k++){//(AS)/(SA)
        if(sb[i+1][i+k-1]){
          (g[i][j]+=(f[i+k][j-1]+g[i+k][j-1])%p)%=p;
        }
        if(sb[j-k+1][j-1]){
          (g[i][j]+=(f[i+1][j-k]+g[i+1][j-k])%p)%=p;
        }
      }
      for(int k=i+1,o=0;k<j-1;k++){
        o=max(o,k+1);
        while(o<j-1&&(s[o]=='*'||s[o]=='?'))o++;
        nxt[k]=min(k+K+1,o);
      }
      int sum=0;
      for(int k=i+2;k<=nxt[i+1];k++)(sum+=g[k][j])%=p;
      (f[i][j]+=(LL)sum*(f[i][i+1]+g[i][i+1])%p)%=p;
      for(int k=i+2;k<j-1;k++){//ASB
        (sum+=(p-g[k][j]))%=p;
        for(int o=nxt[k-1]+1;o<=nxt[k];o++){
          (sum+=g[o][j])%=p;
        }
        (f[i][j]+=(LL)sum*(f[i][k]+g[i][k])%p)%=p;
      }
    }
  }
  printf("%d\n",(f[1][n]+g[1][n])%p);
  KafuuChino HotoKokoa
}

T3

估计难度：普及+。
其实就是找切入点的事。发现枚举第一个数是最左边还是最右边后就可以把数列分成两个口朝两端的栈，每次从栈顶取数。
又发现操作是对称的，当前栈顶的数能取出来当且仅当另一个同样数值的数紧挨最后一个数。
所以可以两边各维护一个双端队列，对于一个数值同时弹掉两个数，如果不能弹就输出 \(-1\)。
巨常数还巨丑代码：

const int N=1000010;
int T,n,a[N],ans[N];
il void Print(){
  int l=1,r=n+n;
  vector<int> qwq;
  for(int i=1;i<=n;i++){
    if(ans[i]==1)putchar('L'),qwq.pub(a[l++]);
    else putchar('R'),qwq.pub(a[r--]);
  }
  for(int i=n-1;~i;i--){
    if(qwq[i]==a[l])putchar('L'),l++;
    else putchar('R'),r--;
  }
  puts("");
}
deque<int> q[2];
il bool Choose(int i){
  if(q[0].size()){
    if(q[0].size()>1&&q[0].front()==q[0].back()){
      ans[i]=1;
      q[0].pop_front(),q[0].pop_back();
    }else if(q[1].size()&&q[0].front()==q[1].front()){
      ans[i]=1;
      q[0].pop_front(),q[1].pop_front();
    }else if(q[1].size()&&q[1].back()==q[0].back()){
      ans[i]=-1;
      q[1].pop_back(),q[0].pop_back();
    }else if(q[1].size()>1&&q[1].back()==q[1].front()){
      ans[i]=-1;
      q[1].pop_back(),q[1].pop_front();
    }else return 0;
  }else {
    if(q[1].size()>1&&q[1].back()==q[1].front()){
      ans[i]=-1;
      q[1].pop_back(),q[1].pop_front();
    }else return 0;
  }
  return 1;
}
int main(){
  Read(T);
  while(T--){
    memset(ans,0,sizeof ans),Read(n);
    for(int i=1;i<=n+n;i++)Read(a[i]);
    q[0].clear(),q[1].clear();
    ans[1]=1;bool ff=1;
    for(int i=2,o=0;i<=n+n;i++){
      if(a[i]==a[1]){
        o=1;continue;
      }
      q[o].push_back(a[i]);
    }
    for(int i=2;i<=n;i++){
      if(!Choose(i)){
        ff=0;break;
      }
    }
    if(ff){
      Print();continue;
    }
    q[0].clear(),q[1].clear(),ans[1]=-1,ff=1;
    for(int i=1,o=0;i<n+n;i++){
      if(a[i]==a[n+n]){
        o=1;continue;
      }
      q[o].push_back(a[i]);
    }
    for(int i=2;i<=n;i++){
      if(!Choose(i)){
        ff=0;break;
      }
    }
    if(ff)Print();
    else puts("-1");
  }
  KafuuChino HotoKokoa
}

T4

估计难度：提高+~省选-
先考虑两个不同色附加点的情况，发现一定是染成黑白两个连通块。观察这时边权和的形式，发现它就是对偶图上两个无界区域之间的最短路（这也是狼抓兔子那题的解法之一）。
现在有多个附加点，显然我们只需要考虑相邻的不同色的点所组成的无界区域。
口胡一下可以发现一定是在这些区域之间两两连不相交的路径，因为如果相交则可以调整到更优。
有了这个结论后就发现无界区域的匹配长得一脸括号匹配的样子，所以我们可以区间 dp。
如图：

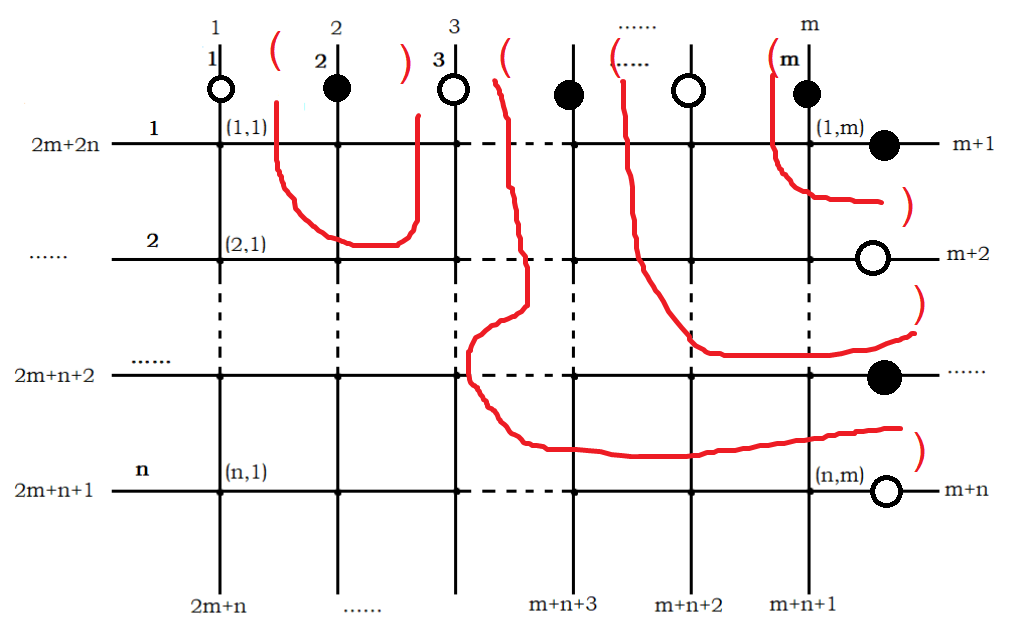
这道题细节非常多而且多测，写的时候一定注意数组大小、边界处理、清空等易错点。
不知道为什么被卡常了，就稍微优化了一下。

const int N=2010;
int n,m,T;
struct Edge {
  int to,nxt,w;
}e[N*N];
int hd[N*N],cn,th[N*N],tcn;
il void ade(int u,int v,int w){
  e[++cn].to=v,e[cn].w=w,e[cn].nxt=hd[u],hd[u]=cn;
}
il int Id(int i,int j){
  return i*(m+1)+j;
}
//x 是射线的编号
il int Get(int x){
  if(x<=m)return Id(0,x);
  else if(x<=m+n)return Id(x-m,m);
  else if(x<=m+n+m)return Id(n,m-(x-m-n));
  else return Id(n-(x-m-n-m),0);
}
vector<int> fr;//所有射线对应的无界区域
int val[N],col[N],bel[N*N];
vector<int> p[N];//无界区域包含的点
int vis[N*N],dis[N*N],f[50][50],g[50][50];
il void Dijkstra(int s,int ttot){
  memset(vis,0,sizeof vis),memset(dis,0x3f,sizeof dis);
  priority_queue<pii > q;
  for(int i:p[s])dis[i]=0,q.push(mkp(0,i));
  int lst=ttot;
  while(!q.empty()){
    if(!lst)break;
    int u=q.top().y;q.pop();
    if(vis[u])continue;
    vis[u]=1;
    if(bel[u]&&g[s][bel[u]]==-1)g[s][bel[u]]=dis[u],lst--;
    for(int i=hd[u];i;i=e[i].nxt){
      int v=e[i].to;
      if(dis[v]>dis[u]+e[i].w){
        dis[v]=dis[u]+e[i].w,q.push(mkp(-dis[v],v));
      }
    }
  }
}
int main(){
  Read(n),Read(m),Read(T);
  for(int i=1;i<=m;i++)fr.pub(Id(0,i));
  for(int i=1;i<=n;i++)fr.pub(Id(i,m));
  for(int i=m;i;i--)fr.pub(Id(n,i-1));
  for(int i=n;i;i--)fr.pub(Id(i-1,0));
  for(int i=0;i<2*(n+m);i++)fr.pub(fr[i]);
  for(int i=1;i<n;i++){
    for(int j=1,x;j<=m;j++){
      Read(x);int u=Id(i,j-1),v=Id(i,j);
      ade(u,v,x),ade(v,u,x);
    }
  }
  for(int i=1;i<=n;i++){
    for(int j=1,x;j<m;j++){
      Read(x);int u=Id(i-1,j),v=Id(i,j);
      ade(u,v,x),ade(v,u,x);
    }
  }
  for(int i=0;i<=Id(n,m);i++)th[i]=hd[i];tcn=cn;
  while(T--){
    memset(bel,0,sizeof bel),memset(col,-1,sizeof col);
    memset(g,-1,sizeof g),memset(val,0,sizeof val);
    for(int i=0;i<=Id(n,m);i++)hd[i]=th[i];cn=tcn;
    int K,tot=0;Read(K);int fck=3;
    for(int i=1,xi,pi,ji;i<=K;i++){
      Read(xi),Read(pi),Read(ji),fck&=(1<<ji);
      col[pi]=ji,val[pi]=xi;
    }
    if(fck){
      puts("0");continue;
    }
    for(int i=1;i<=m;i++){
      int u=Id(0,i-1),v=Id(0,i),w=val[i];
      ade(u,v,w),ade(v,u,w);
    }
    for(int i=1;i<=n;i++){
      int u=Id(i-1,m),v=Id(i,m),w=val[i+m];
      ade(u,v,w),ade(v,u,w);
    }
    for(int i=m;i;i--){
      int u=Id(n,m-i),v=Id(n,m-i+1),w=val[i+m+n];
      ade(u,v,w),ade(v,u,w);
    }
    for(int i=n;i;i--){
      int u=Id(n-i,0),v=Id(n-i+1,0),w=val[i+m+n+m];
      ade(u,v,w),ade(v,u,w);
    }
    for(int i=1;i<=2*(n+m);i++){
      if(col[i]==-1)continue;
      for(int j=i%(2*(n+m))+1;;j=j%(2*(n+m))+1){
        if(col[j]==col[i])break;
        if(col[j]==-1)continue;
        tot++;//括号个数
        for(int k=i-1;;k++){
          int u=fr[k];
          if(u==Get(j))break;
          bel[u]=tot,p[tot].pub(u);
        }
        break;
      }
    }
    for(int i=1;i<=tot;i++)Dijkstra(i,tot);
    memset(f,0x3f,sizeof f);
    for(int i=1;i<=tot;i++)f[i][i]=f[i][i-1]=0;
    f[tot+1][tot]=0;
    for(int l=2;l<=tot;l++){
      for(int i=1;i+l-1<=tot;i++){
        int j=i+l-1;
        for(int k=i+1;k<=j;k+=2){
          f[i][j]=min(f[i][j],\
          f[i+1][k-1]+f[k+1][j]+g[i][k]);
        }
      }
    }
    printf("%d\n",f[1][tot]);
    for(int i=1;i<=tot;i++)p[i].clear();
  }
  KafuuChino HotoKokoa
}