算法竞赛模板 判断线段相交

(1) 快速排斥

就是初步的判断一下，两条线段是不是相交，以两条线段为对角线的矩形，如果不重合的话，那么两条线段一定不可能相交。

                

<1>线段ab的低点低于cd的最高点（可能重合）

<2>cd的最左端小于ab的最右端（可能重合）

<3>cd的最低点低于ab的最高点（加上条件1，两线段在竖直方向上重合）

<4>ab的最左端小于cd的最右端（加上条件2，两直线在水平方向上重合）

综上4个条件，两条线段组成的矩形是重合的。

(2) 跨立实验

如果两条线段相交，那么必须跨立，就是以一条线段为标准，另一条线段的两端点一定在这条线段的两段

即A、B两点在线段CD的两端，C、D两点在线段AB的两端

这里就用到了向量叉积的知识点，有向量叉积的物理意义知：AB x CD=-CD x AB

看下图：

 

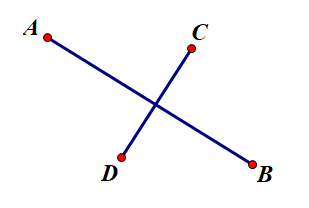
若(CA x CD)·(CB x CD)<=0；

则说明向量CA、CB对于向量CD的方向不同，则A、B在线段CD的两侧，由此可以判断！

#include<bits/stdc++.h>
using namespace std;
struct Node{
    int x,y;
}a,b,c,d;
bool judge(Node a,Node b,Node c,Node d)
{
    //快速排斥 
    if(!(min(a.x,b.x)<=max(c.x,d.x)&&min(c.x,d.x)<=max(a.x,b.x)&&min(a.y,b.y)<=max(c.y,d.y)&&min(c.y,d.y)<=max(a.y,b.y))) 
        return false;
    //跨立实验 
    double u,v,w,z;
    u=(c.x-a.x)*(b.y-a.y)-(b.x-a.x)*(c.y-a.y);  //AC×AB
    v=(d.x-a.x)*(b.y-a.y)-(b.x-a.x)*(d.y-a.y);  //AD×AB
    w=(a.x-c.x)*(d.y-c.y)-(d.x-c.x)*(a.y-c.y);  //CA×AB
    z=(b.x-c.x)*(d.y-c.y)-(d.x-c.x)*(b.y-c.y);  //CB×AB
   
    if(u*v<=1e-9&&w*z<=1e-9)
        return true;
    return false; 
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y>>d.x>>d.y;
        if(judge(a,b,c,d))
            printf("YES
");
        else printf("NO
");
    }
    return 0;
}