http://www.cnblogs.com/keam37/p/3639294.html keam所有 转载请注明出处
Problem Description
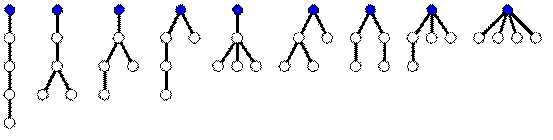
Give you two definitions tree and rooted tree. An undirected connected graph without cycles is called a tree. A tree is called rooted if it has a distinguished vertex r called the root. Your task is to make a program to calculate the number of rooted trees with n vertices denoted as Tn. The case n=5 is shown in Fig. 1.
Input
There are multiple cases in this problem and ended by the EOF. In each case, there is only one integer means n(1<=n<=40) .
Output
For each test case, there is only one integer means Tn.
Sample Input
1 2 5
Sample Output
1 1 9
分析:
题目比较容易读懂,就是求n个节点的树有多少种。
按照递推的思路,f[n]=f[a1]*f[a2]*….f[ai]; 其中 a1+a2+…+ai=n 且a1<=a2<=….<=ai
很自然想到这是整数拆分的样式
进一步考虑,对于n=a*sum[a]+b*sum[b]+c*sum[c]; sum[k]为一个拆分中k的个数
仅对sum[a]个 a计算
一个数a有f[a]种不同的拆分方式
就相当于从(f[a]个不同a)中选取sum[a]个(可以重复) 的排列
即 多重排列 C(f[a]+sum[a]-1,sum[a]);
再依次计算b,c累加即可.
参考代码
#include<iostream>
#define int64 __int64
using namespace std;
int64 f[41];
int cnt[41] , n;
//计算组合数
int64 C(int64 n,int64 m){
m=m<(n-m)?m:(n-m);
int64 ans=1;
for(int i=1;i<=m;i++)
ans=ans*(n-i+1)/i;
return ans;
}
//拆分数并计算f[n]
int dfs(int temp, int left){
if( left == 0 ){
int64 ans = 1;
for(int i = 1; i<=n ;i ++){
if(cnt[i] == 0) continue;
//计算并累加多重排列
ans = ans * C(f[i] + cnt[i] - 1 , cnt[i]);
}
f[n] += ans;
return 0;
}
for(int i=temp;i<=left;i++){
cnt[i]++; dfs(i,left-i);
cnt[i]--;
}
return 0;
}
int main() {
f[1] = f[2] = 1;
for(n = 3; n <= 40 ; n++) dfs(1,n-1);
while(cin>>n) cout<<f[n]<<endl;
return 0;
}