本文章译自OptaPlanner官网上,Geoffrey De Smet先生的博文,链接如下:
https://www.optaplanner.org/blog/2015/06/03/HowGoodAreHumanPlanners.html
在规划方面,我们人类比机器(计算机)更强吗?或者说,自动规划技术能击败人类吗?我与一组软件工程师做了一个实验,结果如下。
实验方法
我让参与者手动解决一个简单的规划问题,向他们讲解规划优化的难度。我给了他们一个旅行商问题(TSP),如下图。让他们连接图上所有点,以找出最短连通路径,并回到原点。

参与者们笑了,他们说这不是一场小孩游戏吗?没错,除了每个点没有编号之外,你也不是在点上找米老鼠(也没有特定的连接要求)。
在纸上计算旅行距离是不现实的,因此,他们基于OptaPlanner中的TSP示例,来研究他们自己的访问方案(即连接方案),以便自动计算路线间的距离。读者也可以自己在TSP示例中尝试一下这个方法,在那个示例中,你用鼠标右键点击一下界面,就可以增加一个点了。
他们首次最佳的尝试,30分钟时间内的方案被记录下来(如下图),这是我们希望得到的最优方案了。最终得到的旅行方案是-674分,也就是说得到的最佳方案,其旅行距离是674.
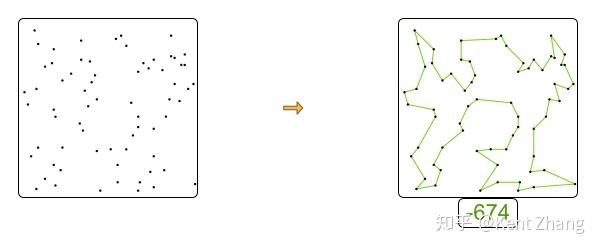
结果
人可以找到约对最优解,包括我在内,大部分人甚至连接接近绝对最优解都找不到。结果如下表:
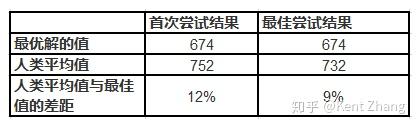
平均上,人类可以找到的最佳路径相对最绝对最佳路径差了9%,若将其反映到实际的车辆运行路线规划工作中,意味着需要多花费9%的时间和油料来完成对所有地点的游历。这是相当高的代价。
这仅仅是一个只有一个约束条件的简单路线规划问题,而在现实世界中,还需要将其它的约束条件考虑进行,例如车辆的运量,现实公路网络限制及一些个性化的业务约束。这些约束将会形成一个更为复杂的问题。
以下是个别情况的规则结果:
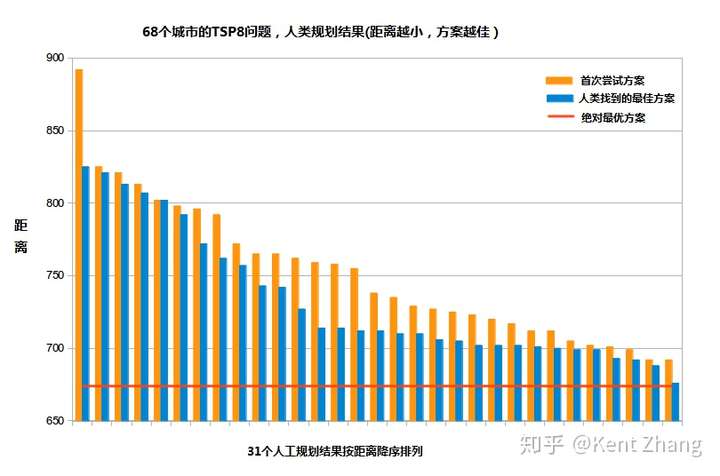
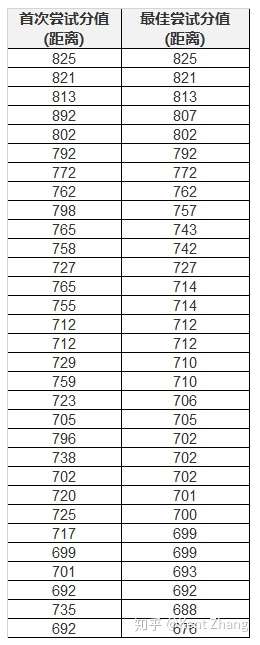 31个人工规划结果
31个人工规划结果
可以看到,最佳的一个人工规划中的最佳结果,比绝对最优解只差了0.3%,这是一个相当好的结果。如果我没记错的话,他花了越过30分钟才能找到这个最佳解。这是一个规划水平的体现,还是运气使然?还是两者结合的结果?结果排行第二的最佳结果,比绝对最佳解差了2%.
通过使用自动规划引擎,例如OptaPlanner, 我们可以在更短的时候内击败人类,可以处理更多的约束和更大的数据值(即处理更多城市的TSP问题)。这是否意味着我们的规划工作,可以摆脱规划人员而自动进行?
我们还需要规划人员吗?
我们仍然需要人工规划,需要规划人员,但并不是用于寻找最优解,而是用来定义寻找什么解。搜索引擎,例如Google可以搜索Web的内容,但它需要人们指定它需要搜索什么信息。类似地,一个自动求解器(包括OptaPlanner)可以优化一个规划工作,但其前提是需要人们告诉它应该优化些什么东西。
在一个非凡的企业里,定义什么业务需要或想要优化,并非易事。这项工作包含大量部门间沟通,业务约束调整等内容。我们仍然需要规划师,因为,随着业务的变化(市场变化,劳工法律变化等引起的业务变化),这些业务约束也需随之改变。同时,我们也需要人工规划师来监控自动规划程序,给程序输入数据并核验规划结果。此外,人们还需保持对规划程的控制。
但我们自问一下,以下两个竞争者,谁能更有机会赢得最终知识测验?
- 地球上最聪明的人。
- 一个平均水平,但可以访问互联网和维基百科的毕业生。
同样地,如果从两个人中选一个,你希望谁在你的组织中做规划优化的工作?一个可以将自动规划引擎作为辅助工具,而别一个人则没有此工具。
本系列文章在公众号不定时连载,请关注公众号(让APS成为可能)及时接收,二维码:

如需了解更多关于Optaplanner的应用,请发电邮致:kentbill@gmail.com
或到讨论组发表你的意见:https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信(13631823503)或QQ(12977379)实时沟通,但因本人日常工作繁忙,通过微信,QQ等工具可能无法深入沟通,较复杂的问题,建议以邮件或讨论组方式提出。(讨论组属于google邮件列表,国内网络可能较难访问,需自行解决)