The Staircases
Memory Limit: 16 MB
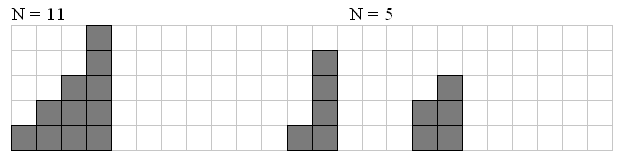
Input
Output
Sample
| input | output |
|---|---|
| 212 | 995645335 |
Problem Source: Ural State University Internal Contest '99 #2
思路分析:
首先声明一下,经过这道题我真的收获很多,包括对递归处理问题易爆栈而且容易超时有了一定程度的认识。而且自己有扩展了数论的知识,确实是一道好题。
我们首先要学习一个数论知识:
数 n 的分划(partition)是将 n 表示成任意多个正整数之和的形式。例如,数 5 的分划如下:
- 5
- 4 + 1
- 3 + 2
- 3 + 1 + 1
- 2 + 2 + 1
- 2 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1
用 p(n) 来记 n 的分划的个数,这样就有 p(5) = 7。
为了求解 p(n),我们引入一个中间函数 p(k, n),表示数 n 的最小被加数不小于 k 的分划的个数。对于给定的 k 值,p(k, n) 正好分为以下两类:
- 最小被加数等于 k
- 最小被加数大于 k
满足第一个条件的分划的个数是 p(k, n − k)。 这是因为,让我们想象数 n − k 的最小被加数不小于 k 的分划,然后将 "+ k" 附加每一个分划后面,就得到数 n 的最小被加数等于 k 的分划。以 n = 5, k = 1 为例,数 4 的最小被加数不小于 1 的分划是 4、3 + 1、2 + 2、2 + 1 + 1 和 1 + 1 + 1 + 1,即 p(k, n − k) = p(1, 4) = 5。然后,将"+ 1" 附加在这 5 个分划后面,就得到数 5 的最小被加数等于 1 的分划:4 + 1、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1 和 1 + 1 + 1 + 1 + 1。
满足第二个条件的分划的个数是 p(k + 1, n) 。以 n = 5, k = 1 为例,数 5 的最小被加数大于 1 的分划是 5 和 3 + 2,即 p(k + 1, n) = p(2, 5) = 2。
也就是说,p(1, 5) = p(2, 5) + p(1, 4)。因此:
- p(k, n) = 0 如果 k > n
- p(k, n) = 1 如果 k = n
- p(k, n) = p(k+1, n) + p(k, n-k) 其它情况
这样,就可以递归地求解 p(k, n),其部分值见下表:
| k | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| n | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 5 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 7 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 11 | 4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 7 | 15 | 4 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 8 | 22 | 7 | 3 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 9 | 30 | 8 | 4 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 10 | 42 | 12 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | |
最后,p(n) = p(1, n)。
现在,让我们的来考虑 将 n 分成不相等的正整数之和的分划。例如,数 8 的分划如下:
- 8
- 7 + 1
- 6 + 2
- 5 + 3
- 5 + 2 + 1
- 4 + 3 + 1
用 q(n) 来记 n 的分划的个数,这样就有 q(8) = 6。
为了求解 q(n),我们引入一个中间函数 q(k, n),表示数 n 的最小被加数不小于 k 的分划的个数。对于给定的 k 值,q(k, n) 正好分为以下两类:
- 最小被加数等于 k
- 最小被加数大于 k
满足第一个条件的分划的个数是 q(k + 1, n − k)。 这是因为,让我们想象数 n − k 的最小被加数大于 k 的分划,然后将 "+ k" 附加每一个分划后面,就得到数 n 的最小被加数等于 k 的分划。以 n = 8, k = 1 为例,数 7 的最小被加数大于 1 的分划是 7、5 + 2 和 4 + 3,即 q(k + 1, n − k) = q(2, 7) = 3。然后,将 "+ 1" 附加在这 3 个分划后面,就得到数 8 的最小被加数等于 1 的分划:7 + 1、5 + 2 + 1 和 4 + 3 + 1。
满足第二个条件的分划的个数是 q(k + 1, n) 。以 n = 8, k = 1 为例,数 8 的最小被加数大于 1 的分划是 8、6 + 2 和 5 + 3,即 q(k + 1, n) = q(2, 8) = 3。
也就是说,q(1, 8) = q(2, 8) + q(2, 7)。因此:
-
- q(k, n) = 0 如果 k > n
- q(k, n) = 1 如果 k = n
- q(k, n) = q(k+1, n) + q(k + 1, n-k) 其它情况
这样,就可以递归地求解 q(k, n),其部分值见下表:
| k | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| n | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 3 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 4 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 7 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 8 | 6 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 9 | 8 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 10 | 10 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
最后,q(n) = q(1, n)。
了解到这里,我们便可以得到递推公式:
- q(k, n) = 0 如果 k > n
- q(k, n) = 1 如果 k = n
- q(k, n) = q(k+1, n) + q(k + 1, n-k) 其它情况
下面我讲讲自己在写代码时出现的问题,自己一开始直接运用的递归公式求解,不仅慢,而且容易出错。
下面我就自己的一段代码拿出来分析分析:
1 long long mean(int n,int k) 2 { 3 for(int i=1;i<=n;i++) 4 { 5 f[i][i]=1;//递归结束条件 6 for(int j=i+1;j<maxn;j++) 7 f[i][j]=0;//递归结束条件,这是写递归函数必备要素 8 } 9 for(int i=2;i<=n;i++) 10 for(int j=i-1;j>=1;j--) 11 f[i][j]=f[i][j+1]+f[i-j][j+1];//这里是重点,我们的递推公式是:f(n,k)=f(n,k+1)+f(n-k,k+1)。因为n是由大到小,所以我们在第一个for循环中必须由小到大写,而k是由小到大,所以我们必须把第二个循环按照由大到小的顺序写 12 return f[n][k];//注意返回值得书写 13 }
这段代码可以保存上一次计算的值,所以计算速度很快,而直接递归的话速度则很慢,需要宠妃计算很多次。下面看看直接递归的代码如何写:
1 long long mean(int n,int k) 2 { 3 if(n==k) return 1; 4 else if(n<k) return 0; 5 else return (mean(n,k+1)+mean(n-k,k+1)); 6 }
AC代码:
#include<iostream> #include<string.h> using namespace std; #define maxn 505 long long f[maxn][maxn]; long long mean(int n,int k) { for(int i=1;i<=n;i++) { f[i][i]=1; for(int j=i+1;j<maxn;j++) f[i][j]=0; } for(int i=2;i<=n;i++) for(int j=i-1;j>=1;j--) f[i][j]=f[i][j+1]+f[i-j][j+1];//这里是重点 return f[n][k]; } int main() { int n; while(cin>>n) { if(n==0) break; cout<<mean(n,1)-1<<endl; } return 0; }