首先说下算法原理:
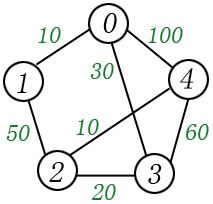
1,设0为源点,建立两个集合S,T,S保存节点0,T集合保存节点1,2,3,4。(S,T是官方定义名称,个人理解S应该是source的缩写,T是target的缩写,看了英文是不是就明白点了)
2,先找出0到其他点最短的点,0到1等于10,即0-1为最短。那么将1添加进S,将1从T中删除。
3,修正路径,这是个难点,怎么修改呢,我举最简单的例子,那就是直接在图上修改。修正路径要修正的是0到其他节点的路径长度,先看下图,
0-1=10
0-2=正无穷,因为0直接到不了2
0-3=30
0-4=100
当我们在S集合中增加了节点1,那么0到其他节点的方式就多了一个,比如0-2,就不在是正无穷,他可以通过1到达,所以0-2=60
那么0-4=100,当0通过1在到达4,结果是0-1-4=10加正无穷,因为1到达不了4,所以10+正无穷就大于100,所以0-4还是100,0-3同理,10+正无穷>30,因此0-3还是30。
1添加进集合S后,在添加次短的节点,因为1是最短的,添加完最短的添加次短的。
现在是0到各节点的路径是:
0-1=10
0-2=60
0-3=30
0-4=100
这里0-3是最短的,因此S集合添加节点3,同样移除T中,3。
添加完3后,再修正路径,因为1已经添加过了所以不在修改1。那么添加2,0-2在上面已经被修正成60了,现在看0-3-2,它等50,小于60,所以0-2再次修正,等于50。0-3不修正,因为是当前选则的路径。接着修改0-4,0-4初始等于100,现在0-3-4等于160,大于100,所以0-4仍然等于100
0-1=10
0-2=50
0-3=30
0-4=100
接着再找最短的,1,3已经选过了,现在最短的是2,0-2=50,通过2在修正,13已经选过不在修正,只修正4,即0-2-4=60(具体流向是0-3-2-4),小于0-4=100,因此修正0-4=60。
最后将4从T中取出添加进S,因为123都已经使用,4不在修正,方法结束,即T为空就结束。
那么0到各点的最短路径为
0-1=10
0-2=50
0-3=30
0-4=60
将上面的算法写成代码如下:
但在学习代码前,首先要理解数组weight是什么,数组weight翻译出来是
第一行 {0,3,2000,7,9999999}
A——>A 宽度(权值)0 自己到自己自然是0
A——>B 宽度(权值)3
A——>C 宽度(权值)2000
A——>D 宽度(权值)7
A——>E 宽度(权值)9999999即无限大,即 到达不了E
第二行 {3,0,4,2,9999999},
B——>A 宽度(权值)3
B——>B 宽度(权值)0 B-B
B——>C 宽度(权值)4
B——>D 宽度(权值)2
B——>E 宽度(权值)9999999 即无限大,即到达不了E
第三行 {9999999,4,0,5,6},
C——>A 宽度(权值)9999999 即无限大 ,即 到达不了A
C——>B 宽度(权值)4
C——>C 宽度(权值)0 C-C
C——>D 宽度(权值)5
C——>E 宽度(权值)6
第四行 {7,2,5,0,4},
D——>A 宽度(权值)7
D——>B 宽度(权值)2
D——>C 宽度(权值)5
D——>D 宽度(权值)0 D-D
D——>E 宽度(权值)4
第五行 {9999999,9999999,4,6,0}
E——>A 宽度(权值)9999999即无限大,即 到达不了A
E——>B 宽度(权值)9999999即无限大,即 到达不了B
E——>C 宽度(权值)4
E——>D 宽度(权值)6
E——>E 宽度(权值)0 E-E
以下为C#代码 可以运行
public class Dijkstra { public static void Excute() { int[][] weight = new int[][] { new int[] {0,3,2000,7,9999999}, new int[] {3,0,4,2,9999999}, new int[] {9999999,4,0,5,6}, new int[] {7,2,5,0,4}, new int[] {9999999,9999999,4,6,0} }; int[] path = Dijsktra(weight, 0); for (int i = 0; i < path.Length; i++) Console.WriteLine(path[i] + " "); } public static int[] Dijsktra(int[][] weight, int start) { //接受一个有向图的权重矩阵,和一个起点编号start(从0编号,顶点存在数组中) //返回一个int[] 数组,表示从start到它的最短路径长度 int n = weight.Length; //顶点个数 int[] shortPath = new int[n]; //存放从start到其他各点的最短路径 int[] visited = new int[n]; //标记当前该顶点的最短路径是否已经求出,1表示已求出 //初始化,第一个顶点求出 shortPath[start] = 0; visited[start] = 1; for (int count = 1; count <= n - 1; count++) //要加入n-1个顶点 { int k = -1; //选出一个距离初始顶点start最近的未标记顶点 int dmin = 1000; for (int i = 0; i < n; i++) { if (visited[i] == 0 && weight[start][i] < dmin) { dmin = weight[start][i]; k = i; } } //将新选出的顶点标记为已求出最短路径,且到start的最短路径就是dmin shortPath[k] = dmin; visited[k] = 1; //以k为中间点想,修正从start到未访问各点的距离 for (int i = 0; i < n; i++) { if (visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]) weight[start][i] = weight[start][k] + weight[k][i]; } } return shortPath; } }
----------------------------------------------------------------------------------------------------
注:此文章为原创,任何形式的转载都请联系作者获得授权并注明出处!
若您觉得这篇文章还不错,请点击下方的【推荐】,非常感谢!
