斯坦福2014机器学习笔记九----支持向量机

一、纲要

　　支持向量机基础及优化目标

　　支持向量机的直观理解

　　核函数

二、内容详述

　　1、支持向量机基础以及优化目标

　　支持向量机(Support Vector Machine)与逻辑回归和神经网络相比，在学习复杂的非线性方程时提供了一种更为清晰，更为强大的方式。这部分我们就从逻辑回归一点点修改来得到本质上的SVM。

　　在前面的内容中，我们知道了逻辑回归的代价函数为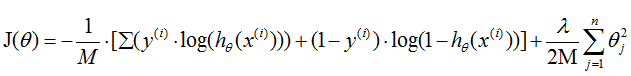，逻辑回归的输出函数为，把h_θ(x)代入代价函数并将负号放进括号里得到 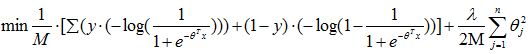，从这个代价函数中我们可以得到y=1和y=0时的结果

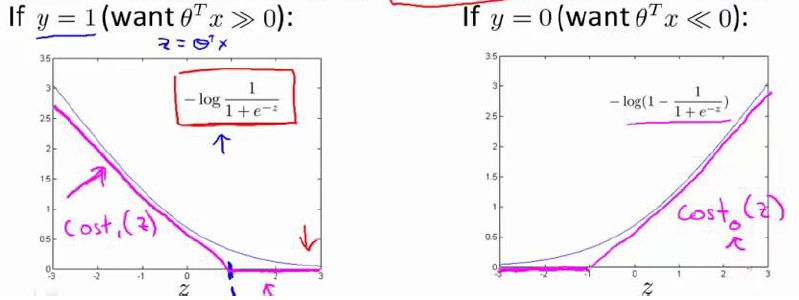
图中的曲线表示逻辑回归的结果，而这段紫红色的线段，包括z=±1左边的部分和z=±1右边的线段就是我们SVM要用的代价函数，即cost1(z)和cost0(z)。有了这些定义之后，我们来构建SVM。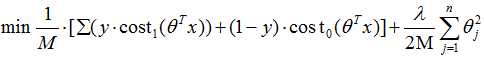这里我们可以先不考虑1/M，因为它是一个常数，不会影响到我们求代价函数的最小化结果。忽略1/M之后，我们可以把第一项看作A，第二项就可以看成λB，所以就变成了A+λB，这是对于逻辑回归来讲是这样的，但是对于SVM，一般都会用CA+B这种形式，这里的C就可以看成是1/λ。对于逻辑回归中如果给λ一个很大的值，那么意味着B就会有很大的权重，而这里对应于给定C一个较小的值，B也意味着有很大的权重。因此，这样就得到了我们SVM中整个优化目标函数，然后最小化这个目标函数，得到SVM学习到的参数C。

　　这里要说明的一点是：SVM的输出相对于逻辑回归是有区别的，SVM的输出直接是0或1，而逻辑回归输出的是y=1的概率。

　　2、SVM的直观理解

　　SVM有时又叫做大间距分类器，只有当θ^Tx≥1时才判断为1，当θ^Tx≤-1时判断为0.跟逻辑回归进行对比，相当于加入了一个安全的间距因子。

那么这个因子会导致什么结果呢？我们接下来用一个特例说明。我们将常数C设置的非常大，那么在目标函数最小化的过程中，第一项CA≈0，所以整个目标函数就剩下了第二项

min 1/2·Σθ_j².这里我们引入一些数学知识来进一步说明。假设θ是一个向量θ=[θ₁,θ₂]^T，我们先不考虑θ₀≠0的情况，也就是说θ₀=0，即截距为0，决策界必须过原点。

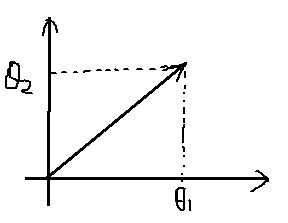向量θ代入目标函数得到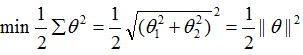，这里的||θ||为θ的范数，即θ的长度。所以SVM所做的全部

事情就是极小化参数θ的范数的平方。

然后我们需要知道向量内积的知识。

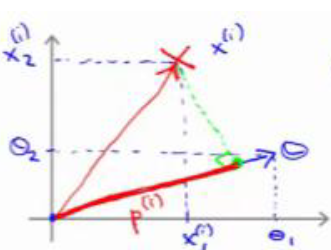
X^Tθ的计算就相当于将向量X投影到向量θ，假设投影长度为图中的红线P⁽ⁱ⁾，那么X^Tθ=P⁽ⁱ⁾||θ||，所以SVM判断分类的条件就可以变成X^Tθ=P⁽ⁱ⁾||θ||≥1，则y=1；若X^Tθ=P⁽ⁱ⁾||θ||≤-1，则y=0.知道了这个，我们来给出一个数据集的例子：假设正负样本分类如图，我们可以看出决策边界其实不止一条

               

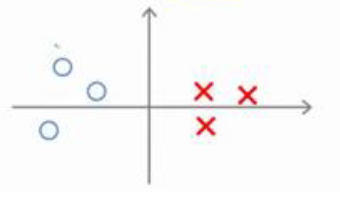
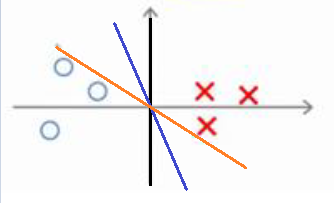
当然，看起来黑色的决策边界才是最好的，事实上SVM所做的就是选择出这样一条最好的决策边界。它是怎么做的呢？

对于这样选择的参数θ，实际上它与决策边界是90度正交的，我们先选择一条不怎么好的决策边界来分析一下。

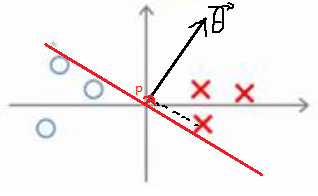
对于这样一条红色的决策边界，我们在进行分类时需要判断X^Tθ=P⁽ⁱ⁾||θ||≥1，从图中可以看出样本在θ上的投影p是很小的，那么p||θ||≥1就需要一个很大的θ，显然这也就不是我们优化目标函数所需要的。然后我们来看下最好的决策边界会有什么样的情况。

对于这条决策边界，θ向量是沿着x轴的，这里再说一下，我们假设θ₀=0，所以θ向量的起点是原点。这样的话样本在θ的投影p就不会很小，X^Tθ=P⁽ⁱ⁾||θ||≥1所需要的θ相对来说就是最小的。这条决策边界与样本之间有更大的最短距离，这个距离叫做间距(margin)，这也是SVM具有鲁棒性的原因，它用一个最大距离来分离样本。所以SVM有时也叫大间距分类器。

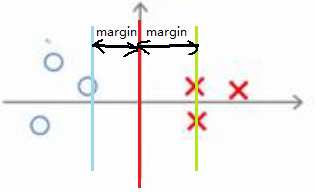
我们这里假设了θ₀=0，即便是θ₀不等于0的情况，SVM所做的都是优化这个目标函数对应着C值非常大的情况，但是可以说明的是，即便θ₀不等于0，SVM仍然可以找到正样本与负样本的大间距分割。

　　3、核函数

　　我们之前讨论过高级数的多项式模型来解决无法用直线分类的问题，如图

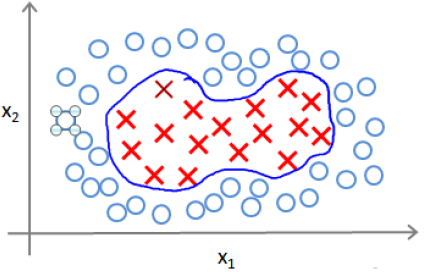
对于这样的分类，我们的模型可能是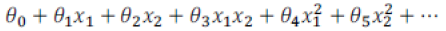形式，那么我们有没有其他办法来解决这样的问题？我们可以利用核函数计算出新的特征。

　　给定一个训练实例X，利用X的各个特征与预先选取的地标(landmark)L1，L2，L3的近似程度来选取新的特征f1,f2,f3。

例如，这里的

||X-l⁽¹⁾||表示X的各个特征与地标L1之间的距离。上式中的similarity(x,l)就是一个核函数，具体来说，这是一个高斯核函数(Gaussian Kernels)。这个地标L1的作用是什么？当训练实例X与地标距离近似为0时，f1 = exp(-0)=1,当X与地标距离很远时，f1 = exp(-(一个很大的数))≈0.同理我们可以计算f2,f3等等。在预测时，我们采用的特征不再是训练实例X本身的特征，而是通过核函数计算出来的新的特征f1,f2,f3。

　　现在我们来说说怎么选取地标？如果有m个训练实例，则我们选取m个地标，且令l⁽¹⁾=X⁽¹⁾，l⁽²⁾=X⁽²⁾，...，l^(m)=X^(m)。那么我们得到的新特征就是建立在原有特征与训练集中所有其他特征之间的距离的基础上，即

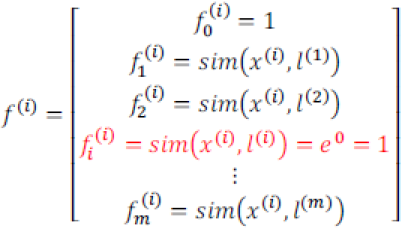
然后我们修改SVM假设为θ^Tf⁽ⁱ⁾≥0，则预测y=1，否则反之。

　　下面我们还需要讨论一下SVM的两个参数C和σ：

　　C=1/λ，λ为正则化参数。这样我们根据前面正则化部分的内容我们得到：

　　　　当C较大时，即λ较小，正则化效果不明显，造成过拟合，高方差

　　　　当C较小时，即λ较大，正则化效果太强，造成欠拟合，高偏差

　　参数σ决定了核函数对附近的点赋予多大的权重。当σ较小时，只有很少的局部点被用于训练模型。

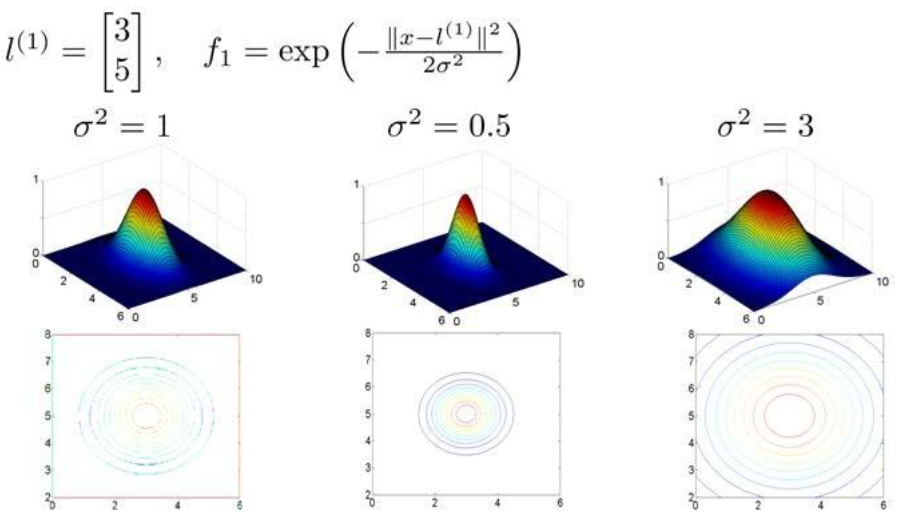
　　σ较大时，可能会导致低方差，高偏差

　　σ较小时，可能会导致低偏差，高方差