说起递归,应该是让我头疼了很久的问题了,在各种问题里都能看见它,而且经常是代码很简单,楞是看不懂。。
关于递归的定义:一个函数自己调用自己,就是递归。对,和一个函数调用其他函数一样,只不过递归是通过反复调用自己来实现的。
所以我们必须先要搞懂函数调用时做了什么。递归和普通函数一样是通过栈实现的,调用函数时,栈内存会往上延深一层工作栈,里面会存放形参、局部变量和返回地址。为什么要放这三个东西呢,传形参是为了让计算机知道当前要处理什么数据,局部变量是执行函数过程需要用到的工具,返回地址是为了方法调用完成后让计算机知道接下来应该执行哪里。函数调用完成前会把返回值存放到栈顶,返回栈顶元素也就是返回值,弹出工作栈,找到返回地址继续执行。
使用递归需要注意的问题:
1.递归应向着问题规模减小的方向进行;
2.一定要有终止条件,不然会无限递归下去。
递归一般有三个作用:
1.解决本来就是用递归形式定义的问题;
2.将问题分解为规模更小的子问题进行求解;
3.代替多重循环。
下面我将举三个例子分别说明递归的这三个作用:
1.解决本来就是用递归形式定义的问题:求n的阶乘(n!)
阶乘的定义是:一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。亦即n!=1×2×3×...×n。阶乘亦可以递归方式定义:0!=1,n!=(n-1)!×n。(摘自百度百科)这个定义就很递归,程序很简单就能写出来。
1 int Factorial(int n) 2 { 3 if (n == 0)//终止条件 4 return 1; 5 else 6 return n * Factorial(n - 1);//问题规模减小 7 }
以求4的阶乘为例,函数调用过程如下(从左到右依次是形参,返回地址用语句表示,返回值):

2.将问题分解为规模更小的子问题进行求解:汉诺塔问题(Hanoi)
古代有一个梵塔, 塔内有三个座A、 B、 C, A座上有64个盘子, 盘子大小不等, 大的在下, 小的在上( 如图)。 有一个和尚想把这64个盘子从A座移到C座, 但每次只能允许移动一个盘子, 并且在移动过程中, 3个座上的盘子始终保持大盘在下, 小盘在上。 在移动过程中可以利用B座, 要求输出移动的步骤。
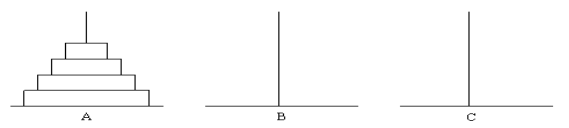
这个问题看起来很复杂,需要注意的有两点:
1.一次只能移动一个盘子
2.移动时大盘子在下,小盘子在上(其实也就是只能移动柱子的最上面那个盘子)
我们可以先假设两种简单的情况:
情况一:假设A柱子上只有一个盘子,很好,直接丢到C柱子上。
情况二:假设A柱子上有两个盘子,先把A柱子上的小盘子移到B柱子,再把A柱子上的大盘子直接移到C柱子,最后把B柱子上的小盘子移到C柱子。
其实不管A柱子上有多少盘子,只要大于两个,我们都可以看成是情况二,只不过中途需要借助其他柱子而已:假设A柱子上有n个盘子,把A柱子上的前n-1个盘子借助C柱子移到B柱子,再把A柱子上的大盘子直接移到C柱子,最后把B柱子上的n-1盘子借助A柱子移到C柱子。
至于如何把A柱子上的前n-1个盘子借助C柱子移到B柱子,和如何把B柱子上的n-1盘子借助A柱子移到C柱子,也可以以同样的方法分成前面的n-2个小盘子和最后一个大盘子,只不过原柱子和目标柱子变了而已,方法是一样的。就这样我们把搬n个盘子的问题分解成了搬前n-1个盘子和第n个盘子的问题,把搬n-1个盘子分解成搬前n-2个盘子和第n-1个盘子的问题......
程序如下:
1 #include<bits/stdc++.h> 2 using namespace std; 3 //把n个盘子从src借助mid移到des 4 void f(int n,char src,char mid ,char des) 5 { 6 if(n==1)//终止条件:只有一个盘子的时候,直接移到目标柱子 7 { 8 cout << src<<"->"<<des<<endl; 9 return ; 10 } 11 //问题规模减小:否则先把src上的n-1个盘子通过des柱子移到mid,再把最后一个盘子直接移到src,再把mid上的n-1个盘子通过src移到des柱子。 12 f(n-1,src,des,mid); 13 f(1,src,mid,des); 14 f(n-1,mid,src,des); 15 } 16 int main() 17 { 18 f(3,'A','B','C');//把3个盘子从A借助B移到C 19 return 0; 20 }
程序输入结果如下:
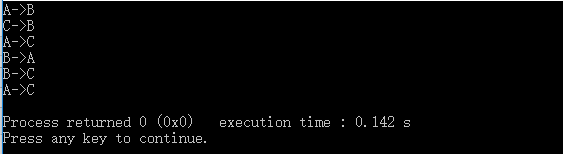
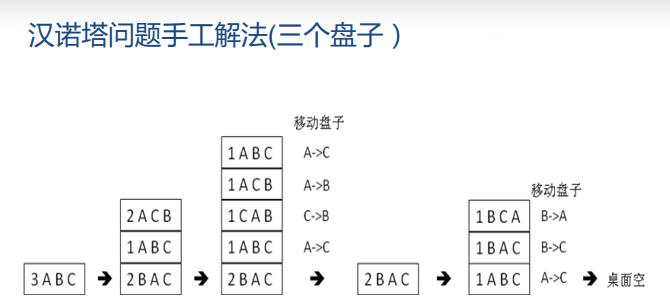
过程推导图如下:
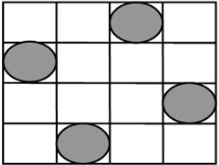
3.代替多重循环:n皇后问题
输入整数n, 要求n个国际象棋的皇后,摆在n*n的棋盘上,互相不能攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,输出全部方案。
比如我们要写一个八皇后问题,暴力是可以做的,写一个八重循环,每一重代表一行,再在循环写出判定条件,如果列相等或行列绝对值相等(即在一个对角线上),就舍弃这个值,应该不难写就不写出代码了,感兴趣的童鞋可以自己写着试试......下面讲一讲递归的做法。
我们要知道所有的循环理论上来说都是可以写成递归的形式的,但是循环有一个致命的缺点,那就是必须要知道需要写几重循环,你无法写出一个不知道大小的循环。就比如N皇后问题,我如果告诉你是四皇后问题,你可以写出四重循环,我说是八皇后问题,你可以写出八重循环,我说是N皇后问题呢?你能写出N重循环去解决这个问题吗?答案是不可以,但是我们可以用递归解决N皇后问题。解决的思路是这样的:以四皇后举例,我们先从第一行的皇后放起,每行从第1列到第4列依次尝试,看看是否与前面各行的皇后冲突,如果都不冲突,将该行皇后放到这个不冲突的位置,再放下一行的皇后,如果第四行能找到与前面的皇后都不冲突的位置,则说明找到了该问题的一个解决方案。
放的过程中也许会有这样的情况:前k-1行的皇后都放好了,但是第k行的皇后怎么都找不到合适的位置,这种情况说明第k-1行的皇后并没有放在真正正确的位置,只保证了与前k-2行的皇后不冲突,但并没有保证以后的皇后有合适的位置可以放置。那就倒回去把第k-1行的皇后再往后放,看有没有其他合适的位置,如果找不到,就说明第k-2行的皇后也没放对,再倒回去把第k-2行的皇后往后挪......这其实就是一个回溯的过程,体现在递归程序中就是一个方法调用完毕后,会回到当初调用这个方法的位置继续执行。这也是为什么递归可以输出全部方案的原因,递归会使得皇后能走的位置都走一遍,即所有行和列的组合都会遍历到,由于是n行xn列,所以也相当于n重循环了(每重循环内部再循环n次)。
程序如下:
1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 int n;//N皇后问题 5 int queenPos[100];//下标代表第几行的皇后,对应的值为该行皇后的列数 6 7 void f(int k) 8 { 9 if(k==n+1)//终止条件:k个皇后都摆放完毕 10 { 11 for(int i = 1;i<=n;++i)//输出一个可行方案 12 { 13 cout <<queenPos[i]<<" "; 14 } 15 cout << endl; 16 return ; 17 } 18 for(int i = 1;i<=n;++i)//皇后可能放置的列数(该循环是程序能输出全部方案的关键) 19 { 20 int j = 0; 21 for(j = 1;j<k;++j)//检查是否与前k-1个皇后冲突 22 { 23 if(i==queenPos[j] || abs(i-queenPos[j])== abs(k-j))//是否在同一列或同一对角线上 24 { 25 break; 26 } 27 } 28 if(j==k)//当前位置i与前k-1个皇后都不冲突 29 { 30 queenPos[k] = i;//将第k个皇后放到第i列 31 f(k+1);//再放第k+1个皇后 32 } 33 }//for(int i = 1;i<=n;++i) 34 35 } 36 int main() 37 { 38 39 cin >>n; 40 f(1);//从第一行的皇后开始放 41 return 0; 42 }
输出如下图:

结束语:我觉得递归的难点在于它和我们平时的思维方式很不一样,是一种计算机的思维。当我们习惯了这种计算机的思维后,递归应该也就不再困难了。
算法小白,理解多有不到之处,还请大家不吝啬多多指教,有问题欢迎到评论区留言。