二分图最大权匹配问题&&KM算法讲解 && HDU 2255 奔小康赚大钱

作者：logosG

链接：https://www.cnblogs.com/logosG/p/logos.html （讲解的KM算法，特别厉害！！！）

KM算法：

现在我们来考虑另外一个问题：如果每个员工做每件工作的效率各不相同，我们如何得到一个最优匹配使得整个公司的工作效率最大呢？

这种问题被称为带权二分图的最优匹配问题，可由KM算法解决。

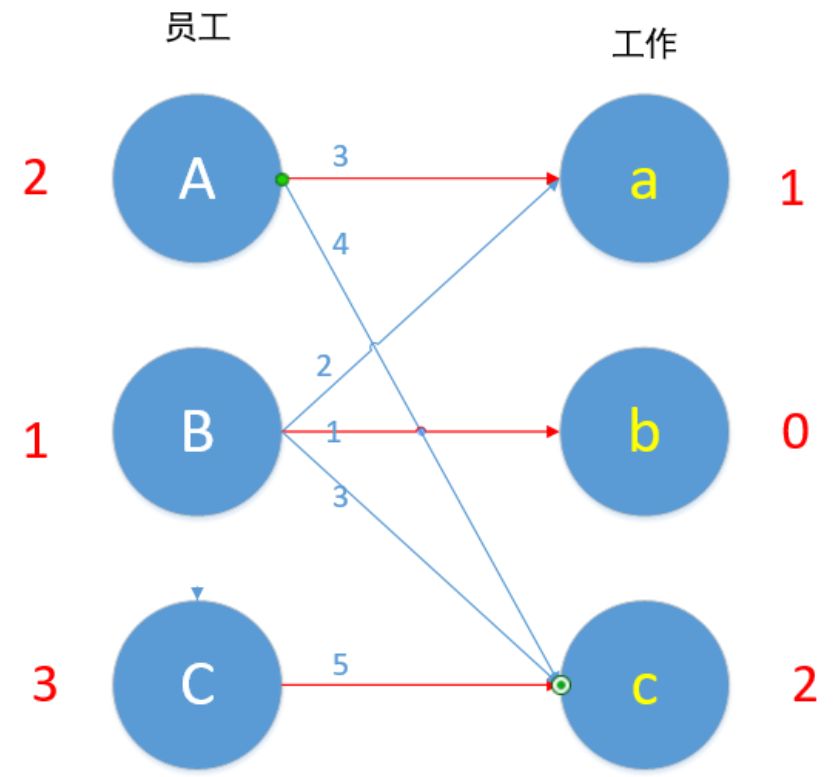
比如上图，A做工作a的效率为3，做工作c的效率为4......以此类推。

不了解KM算法的人如何解决这个问题？我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可。这不失为一个解决方案，但是，如果公司员工的数量越来越多，此种算法的实行难度也就越来越大，我们必须另辟蹊径：KM算法。

KM算法解决此题的步骤如下所示：

1.首先对每个顶点赋值，将左边的顶点赋值为最大权重，右边的顶点赋值为0。

如图，我们将顶点A赋值为其两边中较大的4。

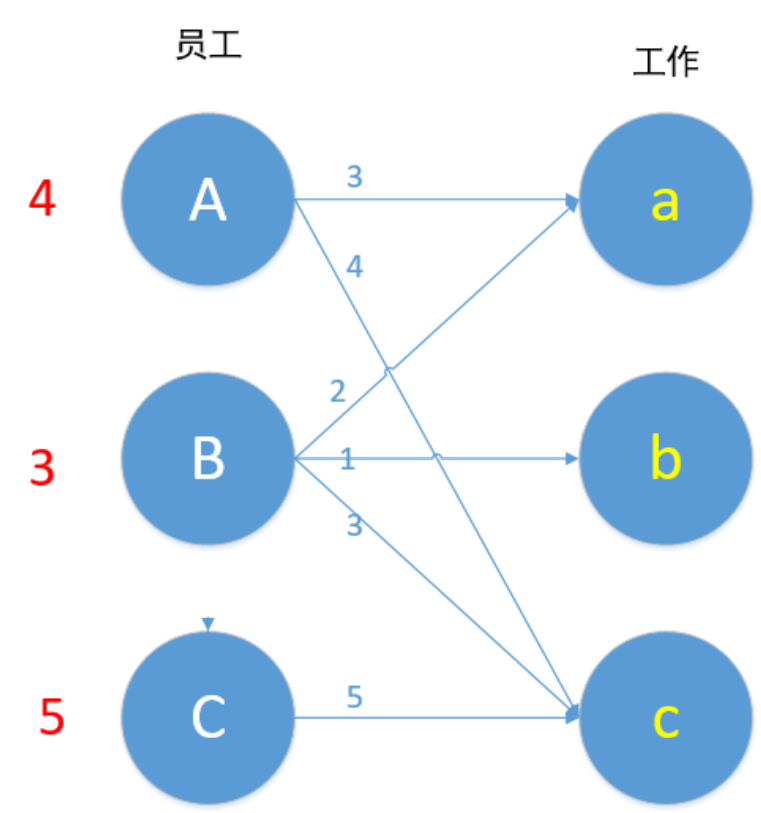
2.进行匹配，我们匹配的原则是：只与权重相同的边匹配，若是找不到边匹配，对此条路径的所有左边顶点-1，右边顶点+1，再进行匹配，若还是匹配不到，重复+1和-1操作。（这里看不懂可以跳过，直接看下面的操作，之后再回头来看这里。）

对A进行匹配，符合匹配条件的边只有Ac边。

匹配成功！

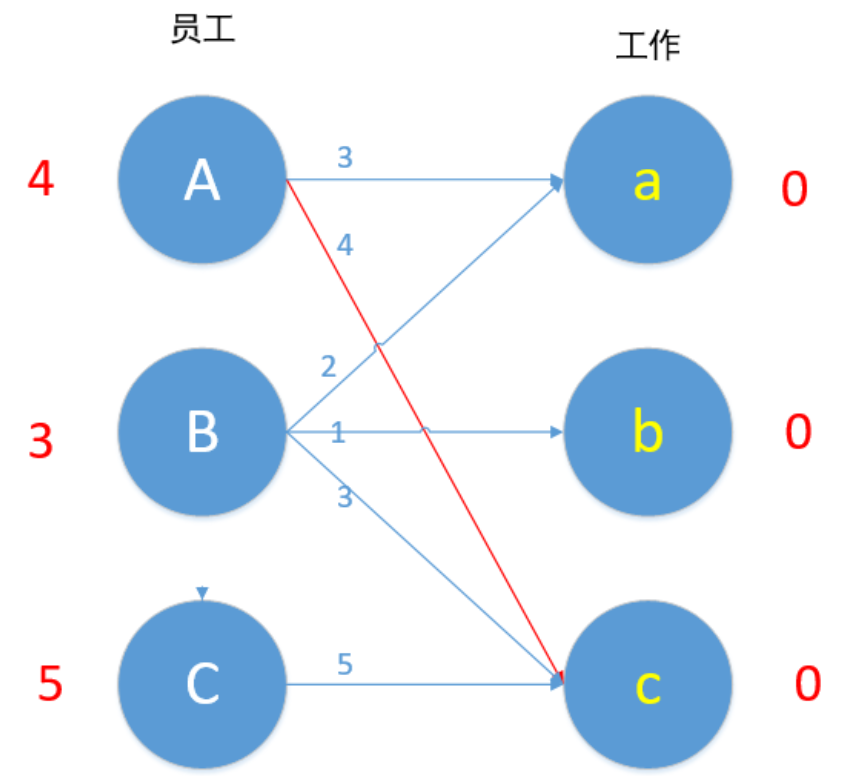
 接下来我们对B进行匹配，顶点B值为3，Bc边权重为3，匹配成~ 等等，A已经匹配c了，发生了冲突，怎么办？我们这时候第一时间应该想到的是，让B换个工作，但根据匹配原则，只有Bc边 3+0=0 满足要求，于是B不能换边了，那A能不能换边呢？对A来说，也是只有Ac边满足4+0=4的要求，于是A也不能换边，走投无路了，怎么办？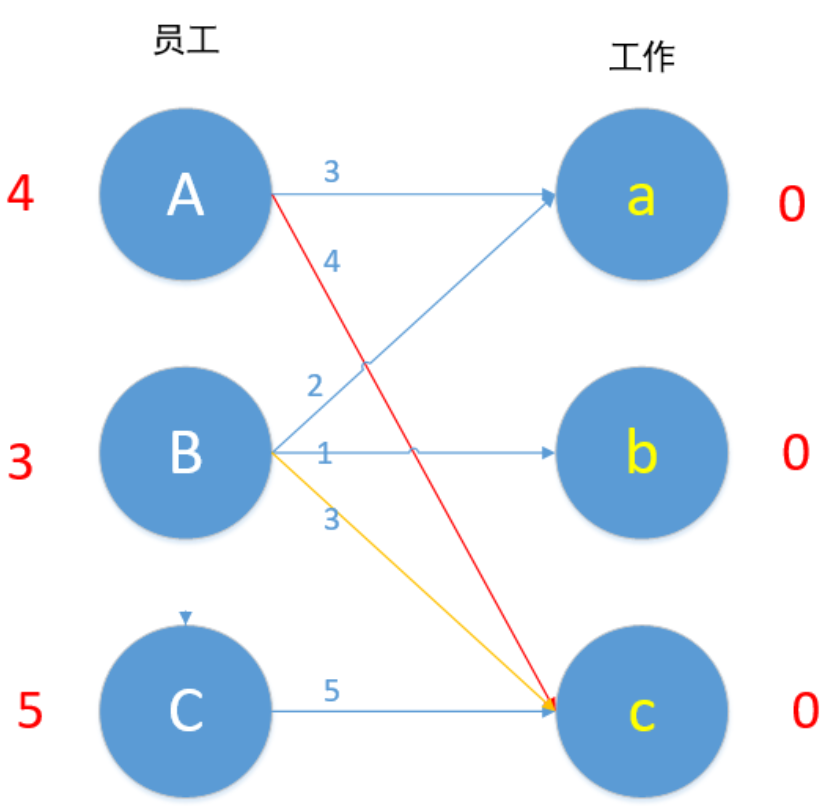

从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个员工找到他们工作效率最高的工作，但是，有些工作会冲突，比如现在，B员工和A员工工作c的效率都是最高，这时我们应该让A或者B换一份工作，但是这时候换工作的话我们只能换到降低总体效率值的工作，也就是说，如果令R=左边顶点所有值相加，若发生了冲突，则最终工作效率一定小于R，但是，我们现在只要求最优匹配，所以，如果A换一份工作降低的工作效率比较少的话，我们是能接受的（对B同样如此）。

在KM算法中如何体现呢？

现在参与到这个冲突的顶点是A,B和c，令所有左边顶点值-1，右边顶点值+1，即 A-1,B-1. c+1，结果如下图所示。

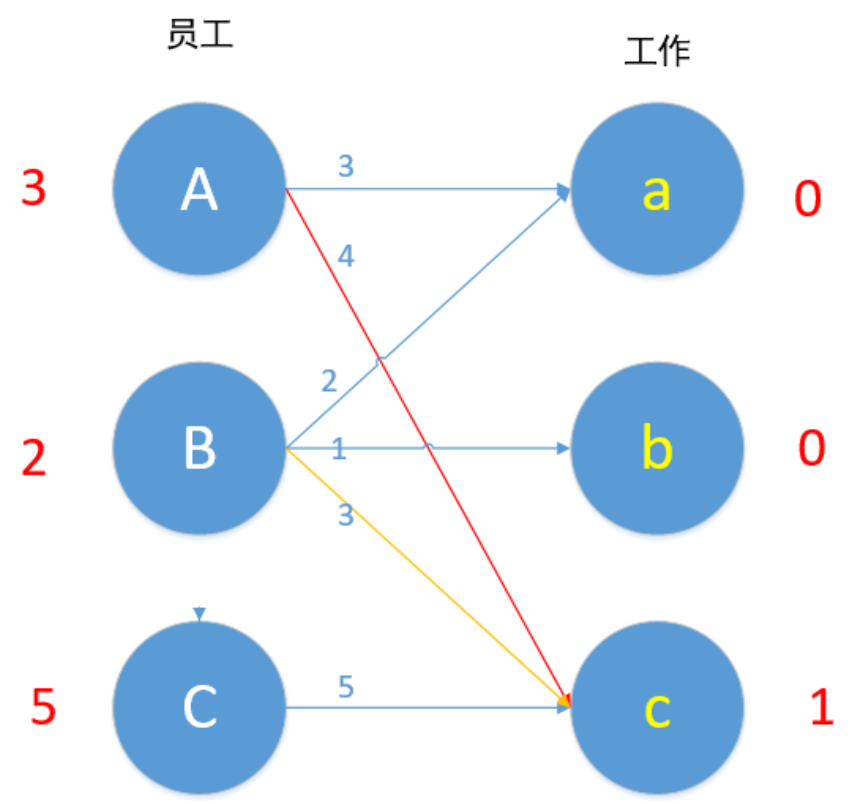
我们进行了上述操作后会发现，若是左边有n个顶点参与运算，则右边就有n-1个顶点参与运算，整体效率值下降了1*（n-（n-1））=1，而对于A来说，Ac本来为可匹配的边，现在仍为可匹配边（3+1=4），对于B来说，Bc本来为可匹配的边，现在仍为可匹配的边（2+1=3），我们通过上述操作，为A增加了一条可匹配的边Aa，为B增加了一条可匹配的边Ba。

现在我们再来匹配，对B来说，Ba边 2+0=2，满足条件，所以B换边，a现在为未匹配状态，Ba匹配！

 我们现在匹配最后一条边C，Cc 5+1！=5，C边无边能匹配，所以C-1。

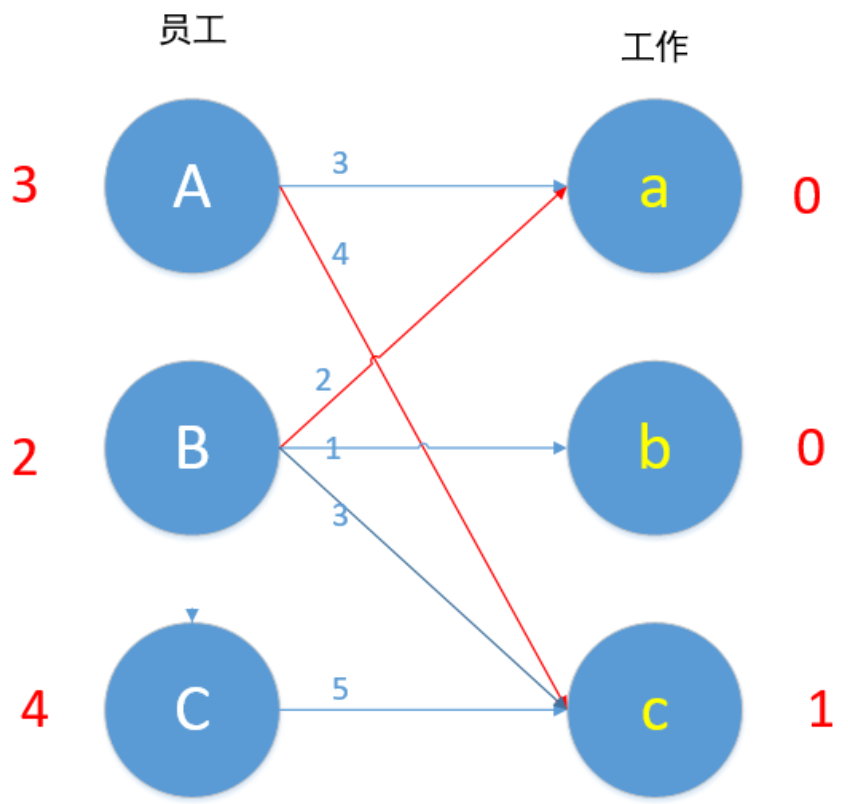
 现在Cc边 4+1=5，可以匹配，但是c已匹配了，发生冲突，C此时不能换边，于是便去找A，对于A来说，Aa此时也为可匹配边，但是a已匹配，A又去找B。

 

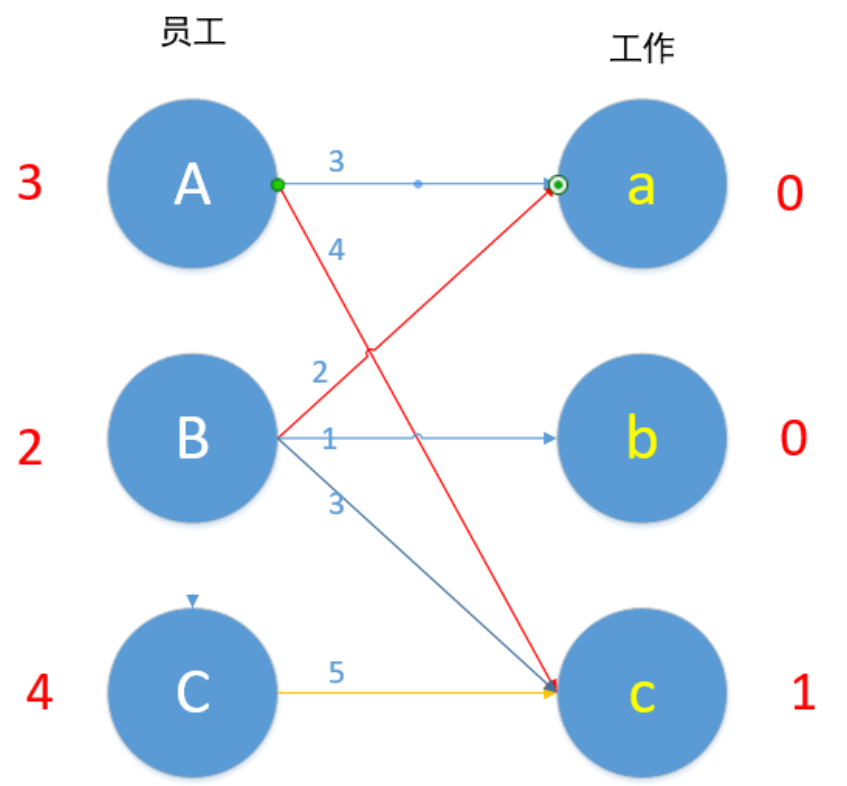
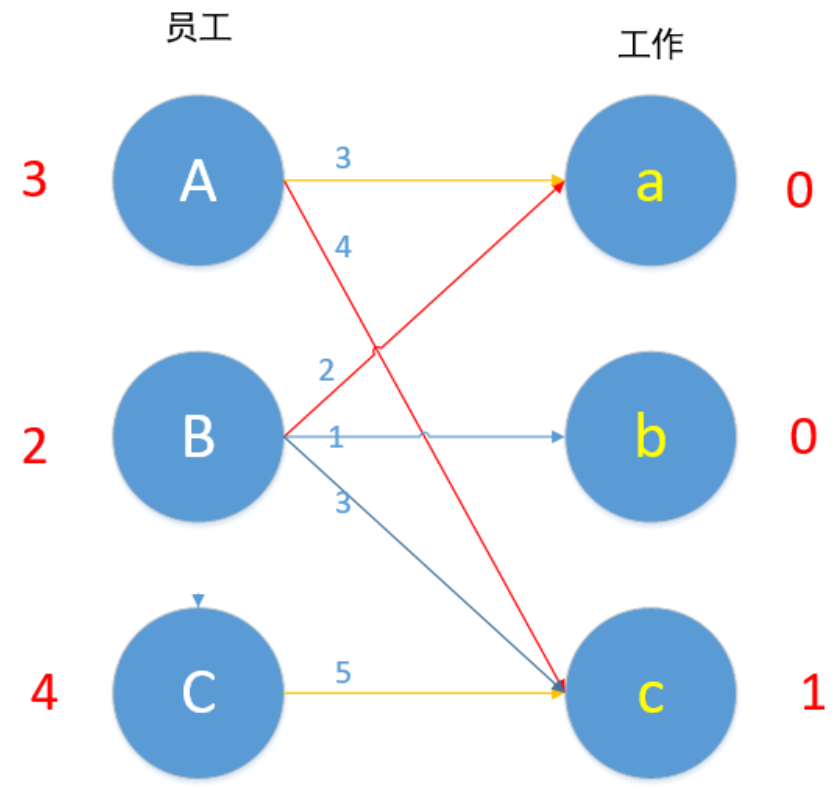
 B现在无边可以匹配了，2+0！=1 ，现在的路径是C→c→A→a→B，所以A-1,B-1,C-1,a+1，c+1。如下图所示。

 对于B来说，现在Bb 1+0=1 可匹配！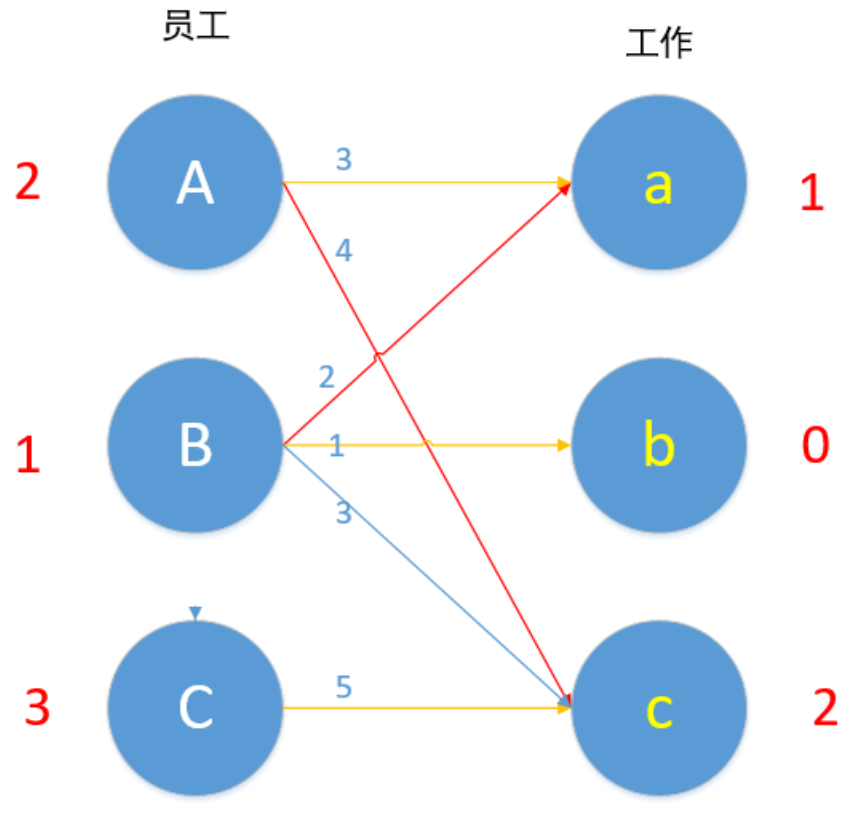

 使用匈牙利算法，对此条路径上的边取反。

如图，便完成了此题的最优匹配。

读者可以发现，这题中冲突一共发生了3次，所以我们一共降低了3次效率值，但是我们每次降低的效率值都是最少的，所以我们完成的仍然是最优匹配！

这就是KM算法的整个过程，整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终我们完成的就是最优匹配！

下面便根据HDU 2255 奔小康赚大钱 给出KM代码：

题意：

n间房子，n个人。每一个人对每一间房子有自己的估价，他们会按照自己的估价买房子。现在你需要将每一间房子分给每一个人，这些人会按照自己的估价给你钱。你需要让最后得到的总钱数最大

题解：

很显然就是一道最大权匹配

代码：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int maxn=510;
const int INF=0x3f3f3f3f;
int n;
int w[maxn][maxn],link[maxn],matchx[maxn],matchy[maxn];
int visitx[maxn],visity[maxn];
int sum[maxn];
int dfs(int x)
{
    visitx[x]=1;
    for(int i=1;i<=n;++i)
    {
        if(visity[i]) continue;
        int temp=matchx[x]+matchy[i]-w[x][i];
        if(!temp)
        {
            visity[i]=1;
            if(link[i]==-1 || dfs(link[i]))
            {
                link[i]=x;
                return 1;
            }
        }
        else if(sum[i]>temp)
            sum[i]=temp;
    }
    return 0;
}
int km()
{
    memset(link,-1,sizeof(link));
    memset(matchy,0,sizeof(matchy));
    for(int i=1;i<=n;++i)
    {
        matchx[i]=-INF;
        for(int j=1;j<=n;++j)
        {
            if(w[i][j]>matchx[i])
                matchx[i]=w[i][j];
        }
    }
    for(int x=1;x<=n;++x)
    {
        for(int i=1;i<=n;++i)
        {
            sum[i]=INF;
        }
        while(1)
        {
            memset(visitx,0,sizeof(visitx));
            memset(visity,0,sizeof(visity));
            if(dfs(x)) break;
            int d=INF;
            for(int i=1;i<=n;++i)
            {
                if(!visity[i]  && d>sum[i])
                    d=sum[i];
            }
            for(int i=1;i<=n;++i)
            {
                if(visitx[i])
                    matchx[i]-=d;
            }
            for(int i=1;i<=n;++i)
            {
                if(visity[i]) matchy[i]+=d;
                else sum[i]-=d;
            }
        }
    }
    int ans=0;
    for(int i=1;i<=n;++i)
    {
        if(link[i]!=-1)
            ans+=w[link[i]][i];
    }
    return ans;
}
int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=1;i<=n;++i)
        {
            for(int j=1;j<=n;++j)
            {
                scanf("%d",&w[i][j]);
            }
        }
        printf("%d
",km());
    }
    return 0;
}

带注释的代码：

#include <iostream>

#include <cstring>

#include <cstdio>

 

using namespace std;

const int MAXN = 305;

const int INF = 0x3f3f3f3f;

 

int love[MAXN][MAXN];   // 记录每个妹子和每个男生的好感度

int ex_girl[MAXN];      // 每个妹子的期望值

int ex_boy[MAXN];       // 每个男生的期望值

bool vis_girl[MAXN];    // 记录每一轮匹配匹配过的女生

bool vis_boy[MAXN];     // 记录每一轮匹配匹配过的男生

int match[MAXN];        // 记录每个男生匹配到的妹子 如果没有则为-1

int slack[MAXN];        // 记录每个汉子如果能被妹子倾心最少还需要多少期望值

 

int N;

 

 

bool dfs(int girl)

{

    vis_girl[girl] = true;

 

    for (int boy = 0; boy < N; ++boy) {

 

        if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次

 

        int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];

 

        if (gap == 0) {  // 如果符合要求

            vis_boy[boy] = true;

            if (match[boy] == -1 || dfs( match[boy] )) {    // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人

                match[boy] = girl;

                return true;

            }

        } else {

            slack[boy] = min(slack[boy], gap);  // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸

        }

    }

 

    return false;

}

 

int KM()

{

    memset(match, -1, sizeof match);    // 初始每个男生都没有匹配的女生

    memset(ex_boy, 0, sizeof ex_boy);   // 初始每个男生的期望值为0

 

    // 每个女生的初始期望值是与她相连的男生最大的好感度

    for (int i = 0; i < N; ++i) {

        ex_girl[i] = love[i][0];

        for (int j = 1; j < N; ++j) {

            ex_girl[i] = max(ex_girl[i], love[i][j]);

        }

    }

 

    // 尝试为每一个女生解决归宿问题

    for (int i = 0; i < N; ++i) {

 

        fill(slack, slack + N, INF);    // 因为要取最小值 初始化为无穷大

 

        while (1) {

            // 为每个女生解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止

 

            // 记录每轮匹配中男生女生是否被尝试匹配过

            memset(vis_girl, false, sizeof vis_girl);

            memset(vis_boy, false, sizeof vis_boy);

 

            if (dfs(i)) break;  // 找到归宿 退出

 

            // 如果不能找到 就降低期望值

            // 最小可降低的期望值

            int d = INF;

            for (int j = 0; j < N; ++j)

                if (!vis_boy[j]) d = min(d, slack[j]);

 

            for (int j = 0; j < N; ++j) {

                // 所有访问过的女生降低期望值

                if (vis_girl[j]) ex_girl[j] -= d;

 

                // 所有访问过的男生增加期望值

                if (vis_boy[j]) ex_boy[j] += d;

                // 没有访问过的boy 因为girl们的期望值降低，距离得到女生倾心又进了一步！

                else slack[j] -= d;

            }

        }

    }

 

    // 匹配完成 求出所有配对的好感度的和

    int res = 0;

    for (int i = 0; i < N; ++i)

        res += love[ match[i] ][i];

 

    return res;

}

 

int main()

{

    while (~scanf("%d", &N)) {

 

        for (int i = 0; i < N; ++i)

            for (int j = 0; j < N; ++j)

                scanf("%d", &love[i][j]);

 

        printf("%d
", KM());

    }

    return 0;

}