模型定义
(感知机)假设输入空间(特征空间)是 ,出空间是
,出空间是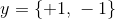 ,
,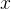 和
和 分属这两个空间,那么由输入空间到输出空间的如下函数:
分属这两个空间,那么由输入空间到输出空间的如下函数:
![]()
称为感知机。其中,![]() 和
和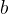 称为感知机模型参数,
称为感知机模型参数,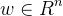 叫做权值或权值向量,
叫做权值或权值向量,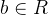 叫做偏置,
叫做偏置, 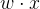 表示向量
表示向量![]() 和
和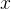 的内积。
的内积。 是一个判别函数:
是一个判别函数:
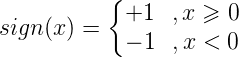
感知机的几何解释是,线性方程

将特征空间划分为正负两个部分:
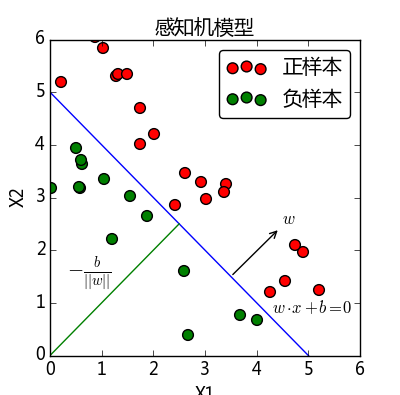
这个平面(2维时退化为直线)称为分离超平面。
感知机学习策略
数据集的线性可分性
定义
给定数据集 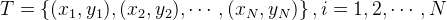
如果存在某个超平面S

能够完全正确地将正负实例点全部分割开来,则称T线性可分,否则称T线性不可分。
感知机学习策略
假定数据集线性可分,我们希望找到一个合理的损失函数。
一个朴素的想法是采用误分类点的总数,但是这样的损失函数不是参数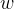 ,
, 的连续可导函数,不可导自然不能把握函数的变化,也就不易优化(不知道 什 么时候该终止训练,或终止的时机不是最优的)。
的连续可导函数,不可导自然不能把握函数的变化,也就不易优化(不知道 什 么时候该终止训练,或终止的时机不是最优的)。
另一个想法是选择所有误分类点到超平面S的总距离。为此,先定义点x0到平面S的距离:
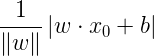
分母 是w的L2范数,所谓L2范数,指的是向量各元素的平方和然后求平方根(长度)。这个式子很好理解,回忆中学学过的点到平面的距离:
是w的L2范数,所谓L2范数,指的是向量各元素的平方和然后求平方根(长度)。这个式子很好理解,回忆中学学过的点到平面的距离:
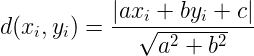
此处的点到超平面S的距离的几何意义就是上述距离在多维空间的推广。
又因为,如果点i被误分类,一定有
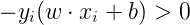
成立,所以我们去掉了绝对值符号,得到误分类点到超平面S的距离公式:
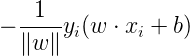
假设所有误分类点构成集合M,那么所有误分类点到超平面S的总距离和:

分母作用不大,反正一定是正的,不考虑分母,就得到了感知机学习的损失函数:
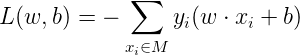
感知机学习算法
原始形式
感知机学习算法是对以下最优化问题的算法:

感知机学习算法是误分类驱动的,先随机选取一个超平面,然后用梯度下降法不断极小化上述损失函数。损失函数的梯度由:
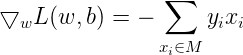
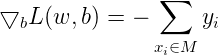
给出。所谓梯度,是一个向量,指向的是标量场增长最快的方向,长度是最大变化率。所谓标量场,指的是空间中任意一个点的属性都可以用一个标量表示的场(个人理解该标量为函数的输出)。
随机选一个误分类点i,对参数w,b进行更新:

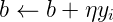
上式 是学习率。损失函数的参数加上梯度上升的反方向,于是就梯度下降了。所以,上述迭代可以使损失函数不断减小,直到为0。于是得到了原始形式的感知机学习算法:
是学习率。损失函数的参数加上梯度上升的反方向,于是就梯度下降了。所以,上述迭代可以使损失函数不断减小,直到为0。于是得到了原始形式的感知机学习算法:
原始算法:

输入:T={(x1,y1),(x2,y2)...(xN,yN)}(其中xi∈X=Rn,yi∈Y={-1, +1},i=1,2...N,学习速率为η)
输出:w, b;感知机模型f(x)=sign(w·x+b)
(1) 初始化w0,b0
(2) 在训练数据集中选取(xi, yi)
(3) 如果yi(w xi+b)≤0
w = w + ηyixi
b = b + ηyi
(4) 转至(2)
Python 代码实现:

#coding = utf-8
import numpy as np
import matplotlib.pyplot as plt
class showPicture:
def __init__(self,data,w,b):
self.b = b
self.w = w
plt.figure(1)
plt.title('Plot 1', size=14)
plt.xlabel('x-axis', size=14)
plt.ylabel('y-axis', size=14)
xData = np.linspace(0, 5, 100)
yData = self.expression(xData)
plt.plot(xData, yData, color='r', label='y1 data')
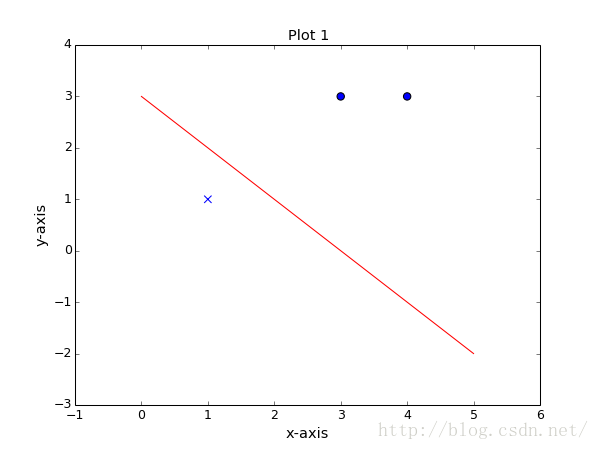
plt.scatter(data[0][0],data[0][1],s=50)
plt.scatter(data[1][0],data[1][1],s=50)
plt.scatter(data[2][0],data[2][1],marker='x',s=50,)
plt.savefig('2d.png',dpi=75)
def expression(self,x):
y = (-self.b - self.w[0]*x)/self.w[1]
return y
def show(self):
plt.show()
class perceptron:
def __init__(self,x,y,a=1):
self.x = x
self.y = y
self.w = np.zeros((x.shape[1],1))
self.b = 0
self.a = 1
def sign(self,w,b,x):
result = 0
y = np.dot(x,w)+b
return int(y)
def train(self):
flag = True
length = len(self.x)
while flag:
count = 0
for i in range(length):
tmpY = self.sign(self.w,self.b,self.x[i,:])
if tmpY*self.y[i]<=0:
tmp = self.y[i]*self.a*self.x[i,:]
tmp = tmp.reshape(self.w.shape)
self.w = tmp +self.w
self.b = self.b + self.y[i]
count +=1
if count == 0:
flag = False
return self.w,self.b
#原始数据
data = [[3,3],[4,3],[1,1]]
xArray = np.array([3,3,4,3,1,1])
xArray = xArray.reshape((3,2))
yArray = np.array([1,1,-1])
#感知机计算权值
myPerceptron = perceptron(x=xArray,y=yArray)
weight,bias = myPerceptron.train()
#画图
picture = showPicture(data,w=weight,b=bias)
picture.show()
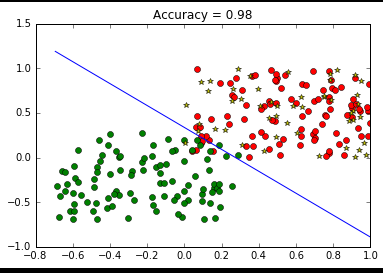
实验效果图:
算法的收敛性
记输入向量加进常数1的拓充形式 ,其最大长度为
,其最大长度为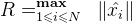 ,记感知机的参数向量
,记感知机的参数向量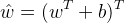 ,设满足条件
,设满足条件 的超平面可以将数据集完全正确地分类,定义最小值伽马:
的超平面可以将数据集完全正确地分类,定义最小值伽马:
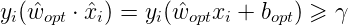
则误分类次数k满足:
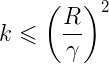
证明请参考《统计学习方法》P31。
感知机学习算法的对偶形式
对偶指的是,将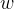 和
和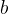 表示为测试数据i的线性组合形式,通过求解系数得到
表示为测试数据i的线性组合形式,通过求解系数得到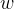 和
和 。具体说来,如果对误分类点i逐步修改
。具体说来,如果对误分类点i逐步修改 ,
,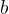 修改了n次,则
修改了n次,则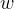 ,
, 关于i的增量分别为
关于i的增量分别为 和
和 ,这里
,这里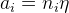 ,则最终求解到的参数分别表示为:
,则最终求解到的参数分别表示为:
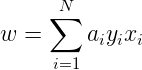

于是有算法2.2:

感知机对偶算法代码

# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
# train matrix
def get_train_data():
M1 = np.random.random((100,2))
# 将label加到最后,方便后面操作
M11 = np.column_stack((M1,np.ones(100)))
M2 = np.random.random((100,2)) - 0.7
M22 = np.column_stack((M2,np.ones(100)*(-1)))
# 合并两类,并将位置索引加到最后
MA = np.vstack((M11,M22))
MA = np.column_stack((MA,range(0,200)))
# 作图操作
plt.plot(M1[:,0],M1[:,1], 'ro')
plt.plot(M2[:,0],M2[:,1], 'go')
# 为了美观,根据数据点限制之后分类线的范围
min_x = np.min(M2)
max_x = np.max(M1)
# 分隔x,方便作图
x = np.linspace(min_x, max_x, 100)
# 此处返回 x 是为了之后作图方便
return MA,x
# GRAM计算
def get_gram(MA):
GRAM = np.empty(shape=(200,200))
for i in range(len(MA)):
for j in range(len(MA)):
GRAM[i,j] = np.dot(MA[i,][:2], MA[j,][:2])
return GRAM
# 方便在train函数中识别误分类点
def func(alpha,b,xi,yi,yN,index,GRAM):
pa1 = alpha*yN
pa2 = GRAM[:,index]
num = yi*(np.dot(pa1,pa2)+b)
return num
# 训练training data
def train(MA, alpha, b, GRAM, yN):
# M 存储每次处理后依旧处于误分类的原始数据
M = []
for sample in MA:
xi = sample[0:2]
yi = sample[-2]
index = int(sample[-1])
# 如果为误分类,改变alpha,b
# n 为学习率
if func(alpha,b,xi,yi,yN,index,GRAM) <= 0:
alpha[index] += n
b += n*yi
M.append(sample)
if len(M) > 0:
# print('迭代...')
train(M, alpha, b, GRAM, yN)
return alpha,b
# 作出分类线的图
def plot_classify(w,b,x, rate0):
y = (w[0]*x+b)/((-1)*w[1])
plt.plot(x,y)
plt.title('Accuracy = '+str(rate0))
# 随机生成testing data 并作图
def get_test_data():
M = np.random.random((50,2))
plt.plot(M[:,0],M[:,1],'*y')
return M
# 对传入的testing data 的单个样本进行分类
def classify(w,b,test_i):
if np.sign(np.dot(w,test_i)+b) == 1:
return 1
else:
return 0
# 测试数据,返回正确率
def test(w,b,test_data):
right_count = 0
for test_i in test_data:
classx = classify(w,b,test_i)
if classx == 1:
right_count += 1
rate = right_count/len(test_data)
return rate
if __name__=="__main__":
MA,x= get_train_data()
test_data = get_test_data()
GRAM = get_gram(MA)
yN = MA[:,2]
xN = MA[:,0:2]
# 定义初始值
alpha = [0]*200
b = 0
n = 1
# 初始化最优的正确率
rate0 = 0
# print(alpha,b)
# 循环不同的学习率n,寻求最优的学习率,即最终的rate0
# w0,b0为对应的最优参数
for i in np.linspace(0.01,1,100):
n = i
alpha,b = train(MA, alpha, b, GRAM, yN)
alphap = np.column_stack((alpha*yN,alpha*yN))
w = sum(alphap*xN)
rate = test(w,b,test_data)
# print(w,b)
rate = test(w,b,test_data)
if rate > rate0:
rate0 = rate
w0 = w
b0 = b
print('Until now, the best result of the accuracy on test data is '+str(rate))
print('with w='+str(w0)+' b='+str(b0))
print('---------------------------------------------')
# 在选定最优的学习率后,作图
plot_classify(w0,b0,x,rate0)
plt.show()
实验效果图: