Mine
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 51 Accepted Submission(s): 6
Problem Description
Have you ever played a game in Windows: Mine?
This game is played on a n*m board, just like the Pic(1)
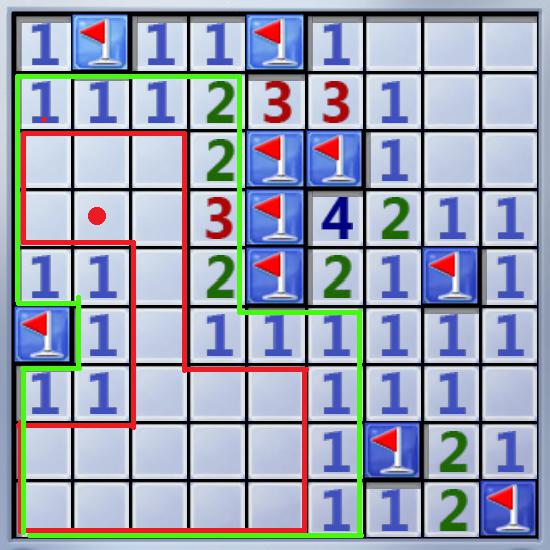

On the board, Under some grids there are mines (represent by a red flag). There are numbers ‘A(i,j)’ on some grids means there’re A(i,j) mines on the 8 grids which shares a corner or a line with gird(i,j). Some grids are blank means there’re no mines on the 8 grids which shares a corner or a line with them.
At the beginning, all grids are back upward.
In each turn, Player should choose a back upward grid to click.
If he clicks a mine, Game over.
If he clicks a grid with a number on it , the grid turns over.
If he clicks a blank grid, the grid turns over, then check grids in its 8 directions.If the new grid is a blank gird or a grid with a number,it will be clicked too.
So If we click the grid with a red point in Pic(1), grids in the area be encompassed with green line will turn over.
Now Xiemao and Fanglaoshi invent a new mode of playing Mine. They have found out coordinates of all grids with mine in a game. They also find that in a game there is no grid will turn over twice when click 2 different connected components.(In the Pic(2), grid at (1,1) will turn over twice when player clicks (0,0) and (2,2) , test data will not contain these cases).
Then, starting from Xiemao, they click the grid in turns. They both use the best strategy. Both of them will not click any grids with mine, and the one who have no grid to click is the loser.
Now give you the size of board N, M, number of mines K, and positions of every mine Xi,Yi. Please output who will win.
This game is played on a n*m board, just like the Pic(1)


On the board, Under some grids there are mines (represent by a red flag). There are numbers ‘A(i,j)’ on some grids means there’re A(i,j) mines on the 8 grids which shares a corner or a line with gird(i,j). Some grids are blank means there’re no mines on the 8 grids which shares a corner or a line with them.
At the beginning, all grids are back upward.
In each turn, Player should choose a back upward grid to click.
If he clicks a mine, Game over.
If he clicks a grid with a number on it , the grid turns over.
If he clicks a blank grid, the grid turns over, then check grids in its 8 directions.If the new grid is a blank gird or a grid with a number,it will be clicked too.
So If we click the grid with a red point in Pic(1), grids in the area be encompassed with green line will turn over.
Now Xiemao and Fanglaoshi invent a new mode of playing Mine. They have found out coordinates of all grids with mine in a game. They also find that in a game there is no grid will turn over twice when click 2 different connected components.(In the Pic(2), grid at (1,1) will turn over twice when player clicks (0,0) and (2,2) , test data will not contain these cases).
Then, starting from Xiemao, they click the grid in turns. They both use the best strategy. Both of them will not click any grids with mine, and the one who have no grid to click is the loser.
Now give you the size of board N, M, number of mines K, and positions of every mine Xi,Yi. Please output who will win.
Input
Multicase
The first line of the date is an integer T, which is the number of the text cases. (T<=50)
Then T cases follow, each case starts with 3 integers N, M, K indicates the size of the board and the number of mines.Then goes K lines, the ith line with 2 integer Xi,Yi means the position of the ith mine.
1<=N,M<=1000 0<=K<=N*M 0<=Xi<N 0<=Yi<M
The first line of the date is an integer T, which is the number of the text cases. (T<=50)
Then T cases follow, each case starts with 3 integers N, M, K indicates the size of the board and the number of mines.Then goes K lines, the ith line with 2 integer Xi,Yi means the position of the ith mine.
1<=N,M<=1000 0<=K<=N*M 0<=Xi<N 0<=Yi<M
Output
For each case, first you should print "Case #x: ", where x indicates the case number between 1 and T . Then output the winner of the game, either ”Xiemao” or “Fanglaoshi”. (without quotes)
Sample Input
2
3 3 0
3 3 1
1 1
Sample Output
Case #1: Xiemao
Case #2: Fanglaoshi
Source
Recommend
zhuyuanchen520
明显的SG博弈。
首先分块。连通的空白块和相连的数字块是一起的,一个单独的数字块是一类。
单独一个的数组块,SG是1.
空白块+若干个数字块,数字块个数为n的话,SG是n%2 + 1
然后bfs解决就可以了
1 /* *********************************************** 2 Author :kuangbin 3 Created Time :2013/8/15 13:25:56 4 File Name :F:2013ACM练习2013多校81003.cpp 5 ************************************************ */ 6 7 #include <stdio.h> 8 #include <string.h> 9 #include <iostream> 10 #include <algorithm> 11 #include <vector> 12 #include <queue> 13 #include <set> 14 #include <map> 15 #include <string> 16 #include <math.h> 17 #include <stdlib.h> 18 #include <time.h> 19 using namespace std; 20 const int MAXN = 1010; 21 bool g[MAXN][MAXN]; 22 int move[][2] = {{0,1},{0,-1},{-1,0},{1,0},{1,1},{1,-1},{-1,1},{-1,-1}}; 23 bool used[MAXN][MAXN]; 24 int n,m; 25 bool check(int x,int y) 26 { 27 if(x > 0 && g[x-1][y])return true; 28 if(x < n-1 && g[x+1][y])return true; 29 if(y > 0 && g[x][y-1])return true; 30 if(y < m-1 && g[x][y+1])return true; 31 if(x > 0 && y > 0 && g[x-1][y-1])return true; 32 if(x > 0 && y < m-1 && g[x-1][y+1])return true; 33 if(x < n-1 && y > 0 && g[x+1][y-1])return true; 34 if(x < n-1 && y < m-1 && g[x+1][y+1])return true; 35 return false; 36 } 37 int dfs(int x,int y) 38 { 39 queue<pair<int,int> >q; 40 q.push(make_pair(x,y)); 41 int cnt = 0; 42 used[x][y] = true; 43 while(!q.empty()) 44 { 45 pair<int,int> tmp = q.front(); 46 q.pop(); 47 int nx = tmp.first; 48 int ny = tmp.second; 49 if(check(nx,ny)) 50 { 51 cnt++; 52 continue; 53 } 54 for(int i = 0;i < 8;i++) 55 { 56 int tx = nx + move[i][0]; 57 int ty = ny + move[i][1]; 58 if(tx < 0 || tx >= n || ty < 0|| ty >= m)continue; 59 if(used[tx][ty])continue; 60 if(g[tx][ty])continue; 61 q.push(make_pair(tx,ty)); 62 used[tx][ty] = true; 63 } 64 } 65 return cnt; 66 } 67 68 int main() 69 { 70 //freopen("in.txt","r",stdin); 71 //freopen("out.txt","w",stdout); 72 int T; 73 scanf("%d",&T); 74 int iCase = 0; 75 while(T--) 76 { 77 iCase ++; 78 int k; 79 scanf("%d%d%d",&n,&m,&k); 80 memset(g,false,sizeof(g)); 81 int x,y; 82 while(k--) 83 { 84 scanf("%d%d",&x,&y); 85 g[x][y] = true; 86 } 87 memset(used,false,sizeof(used)); 88 int ans = 0; 89 for(int i = 0;i < n;i++) 90 for(int j = 0 ;j < m;j++) 91 if(!g[i][j] && !used[i][j] && !check(i,j)) 92 { 93 int tmp = dfs(i,j); 94 ans ^= (tmp%2+1); 95 } 96 for(int i = 0;i < n;i++) 97 for(int j = 0;j < m;j++) 98 if(!g[i][j] && !used[i][j] && check(i,j)) 99 ans ^= 1; 100 if(ans == 0)printf("Case #%d: Fanglaoshi ",iCase); 101 else printf("Case #%d: Xiemao ",iCase); 102 } 103 104 return 0; 105 }