选择类的排序算法
简单选择排序算法
采用最简单的选择方式，从头到尾扫描待排序列，找一个最小的记录（递增排序），和第一个记录交换位置，再从剩下的记录中继续反复这个过程，直到全部有序。
具体过程：
首先通过 n –1 次关键字比较，从 n 个记录中找出关键字最小的记录，将它与第一个记录交换。
再通过 n –2 次比较，从剩余的 n –1 个记录中找出关键字次小的记录，将它与第二个记录交换。
如图
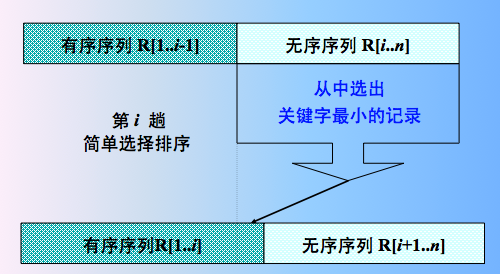
过程图解
令 k=i；j = i + 1；
目的是使用 k 找出剩余的 n-1个记录中，一趟排序的最值，如果 j 记录小于 k 记录，k=j；
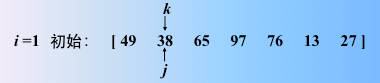
继续比较，j++，如果 j 记录不小于 k 记录，继续 j++，这里使用 k 来找出一趟排序的最值
直到 j=n 为止
交换k 记录和第 i 个记录（i 从头开始的），然后 i++，进行下一趟选择排序过程
整个过程图示
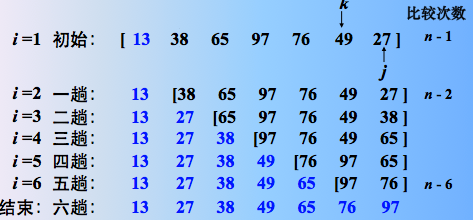
直到无序序列为0为止
代码如下：
1 //简单选择递增排序 2 void selectSort(int List[], int len) 3 { 4 //简单选择排序的循环 5 for (int i = 0; i < len; i++) { 6 int k = i; 7 //一次排序过程，终止条件是 j 扫描到了最后一个记录处 8 for (int j = i + 1; j <= len; j++) { 9 if (List[j] < List[k]) { 10 k = j; 11 } 12 } 13 //扫描完毕，交换最值，先判断是否重复 14 if (i != k) { 15 //交换 16 List[i] = List[i] + List[k]; 17 List[k] = List[i] - List[k]; 18 List[i] = List[i] - List[k]; 19 }// end of if 20 }//end of for 21 } 22 23 int main(void) 24 { 25 26 int source[7] = {49, 38, 65, 97, 76, 13, 27}; 27 28 selectSort(source, 7); 29 30 for (int i = 1; i < 8; i++) { 31 printf(" %d ", source[i]); 32 } 33 34 return 0; 35 }
13 27 38 49 65 76 97 Program ended with exit code: 0
空间复杂度:O(1)
比较次数:
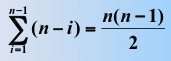
时间复杂度：O(n^2)
简单选择排序的稳定性：不稳定
锦标赛排序和树形选择排序
锦标赛排序也叫树形选择排序，是一种按照锦标赛的思想进行选择的排序方法，该方法是在简单选择排序方法上的改进。简单选择排序，花费的时间大部分都浪费在值的比较上面，而锦标赛排序刚好用树保存了前面比较的结果，下一次比较时直接利用前面比较的结果，这样就大大减少比较的时间，从而降低了时间复杂度，由O(n^2)降到O(nlogn)，但是浪费了比较多的空间，“最大的值”也比较了多次。
大概过程如下：
首先对n个记录进行两两比较，然后优胜者之间再进行两两比较，如此重复，直至选出最小关键字的记录为止。
类似甲乙丙三队比赛，前提是有这样一种传递关系：若乙胜丙，甲胜乙，则认为甲必能胜丙。
锦标赛排序图解如下
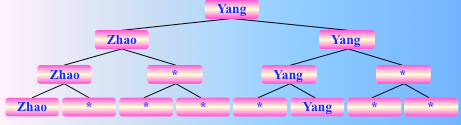
初始序列，这么多队伍参加比赛
两两比较之，用一个完全二叉树表示，反复直到一趟比较后，选出冠军
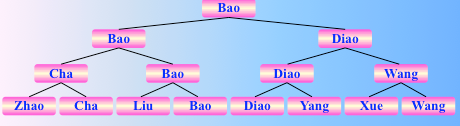
找到了 bao，是冠军，选出冠军的比较次数为 2^2+2^1+2^0 = 2^3 -1 = n-1，然后继续比较，把原始序列的 bao 去掉
选了 cha，选出亚军的比较次数为 3，即 log2 n 次。 同理，把 cha 去掉，继续两两比较
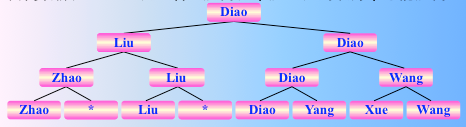
找到了 diao，其后的 n-2 个人的名次均如此产生
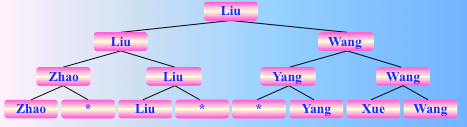
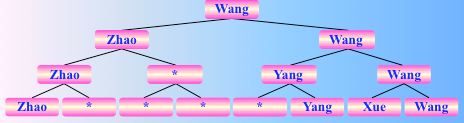
所以对于 n 个参赛选手来说，即对 n 个记录进行锦标赛排序，总的关键字比较次数至多为 (n-1)log2 n + n -1，故时间复杂度为： O(nlogn)。
此法除排序结果所需的 n 个单元外，尚需 n-1 个辅助单元。
这个过程可用一棵有n个叶子结点的完全二叉树表示，根节点中的关键字即为叶子结点中的最小关键字。在输出最小关键字之后，根据关系的可传递性，欲选出次小关键字， 仅需将叶子结点中的最小关键字改为“最大值”，如∞，然后从该叶子结点开始，和其左（右）兄弟的关键字进行比较，修改从叶子结点到根的路径上各结点的关键字，则根结点的关键字即为次小关键字。也就是所谓的树形选择排序，这种算法的缺点在于：辅助存储空间较多、最大值进行多余的比较。
树形选择排序
思想：首先对 n 个记录的关键字进行两两比较，然后在其中 不大于 n/2 的整数个较小者之间再进行两两比较，直到选出最小关键字的记录为止。可以用一棵有 n 个叶子结点的完全二叉树表示。
树形选择排序图解如下：
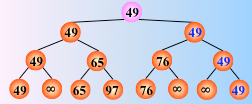
对 n 个关键字两两比较，直到选出最小关键字为止，一趟排序结束
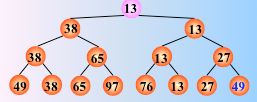
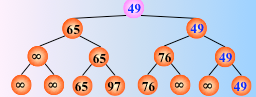
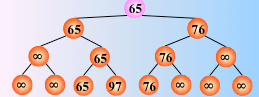
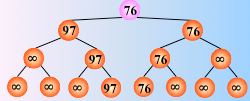
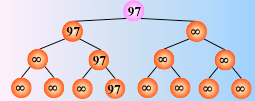
反复这个过程，仅需将叶子结点的最小关键字改为最大值∞，即可
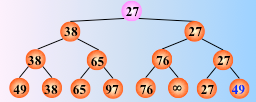
然后从该叶子结点开始，继续和其左右兄弟的关键字比较，找出最值
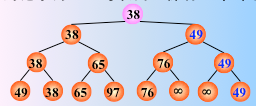
时间复杂度：由于含有 n 个叶子结点的完全二叉树的深度为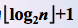
，则在树形选择排序中，除了最小关键字外，每选择一个次小关键字仅需进行 
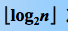次比较，故时间复杂度为 O(n logn)。
缺点： 1、与“∞”的比较多余； 2、辅助空间使用多。
为了弥补这些缺点，1964年，堆排序诞生。
堆排序
堆的定义：n 个元素的序列 (k1, k2, …, kn)，当且仅当满足下列关系：任何一个非终端结点的值都大于等于（或小于等于）它左右孩子的值时，称之为堆。若序列{k1,k2,…,kn}是堆，则堆顶元素（即完全二叉树的根）必为序列中n个元素的最小值（或最大值） 。
可将堆序列看成完全二叉树，则： k2i 是 ki 的左孩子； k2i+1 是 ki 的右孩子。所有非终端结点的值均不大（小）于其左右孩子结点的值。堆顶元素必为序列中 n 个元素的最小值或最大值。
若：ki <= k2i ， ki <= k2i+1，也就是说父小孩大，则为小顶堆（小根堆，正堆），反之，父大孩小，叫大顶堆（大根堆，逆堆）
堆排序定义：将无序序列建成一个堆，得到关键字最小（大）的记录；输出堆顶的最小（大）值后，将剩余的 n-1 个元素重又建成一个堆，则可得到 n 个元素的次小值；如此重复执行，直到堆中只有一个记录为止，每个记录出堆的顺序就是一个有序序列，这个过程叫堆排序。
堆排序需解决的两个问题：
1、如何由一个无序序列建成一个堆？
2、在输出堆顶元素后，如何将剩余元素调整为一个新的堆？
第二个问题解决方法——筛选：
所谓“筛选”指的是，对一棵左/右子树均为堆的完全二叉树，“调整”根结点使整个二叉树也成为一个堆。具体是：输出堆顶元素之后，以堆中最后一个元素替代之；然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换；重复上述操作，直至叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为“筛选”。
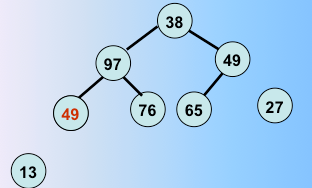
例： (13, 38, 27, 49, 76, 65, 49, 97)
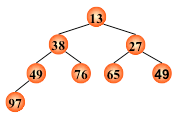
输出堆顶元素之后，以堆中最后一个元素替代之；
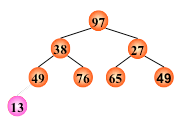
然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换
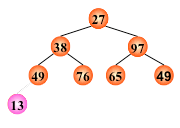
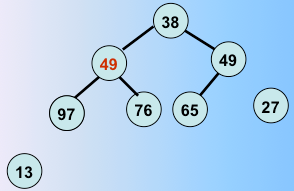
输出堆顶元素之后，以堆中最后一个元素替代之；
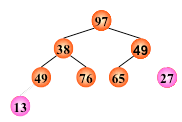
然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换
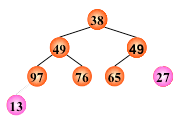
输出堆顶元素之后，以堆中最后一个元素替代之；
然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换
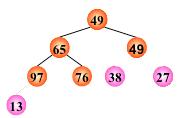
输出堆顶元素之后，以堆中最后一个元素替代之；
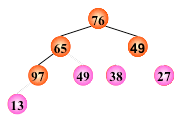
然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换
输出堆顶元素之后，以堆中最后一个元素替代之；
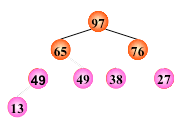
然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换
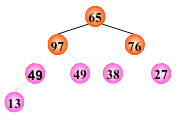
对深度为 k 的堆，“筛选”所需进行的关键字比较的次数至多为 2(k-1)。
第一个问题解决方法：从无序序列的第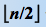 
个元素（即无序序列对应的完全二叉树的最后一个内部结点）起，至第一个元素止，进行反复筛选。建堆是一个从下往上进行“筛选”的过程。把原始的序列一一对应的（从左到右，从上到下）建立一个完全二叉树即可，然后建立小顶堆（大顶堆）
建堆
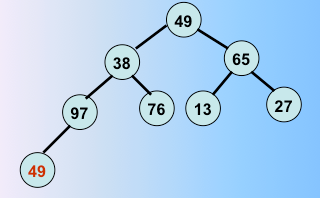
调整，筛选过程
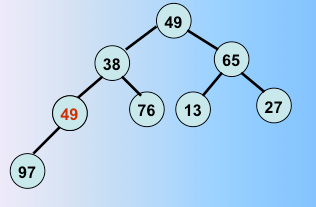
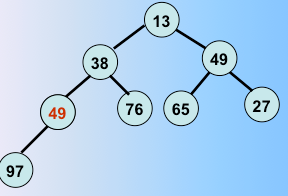
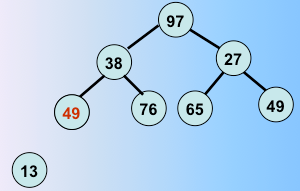
一趟堆排序完毕，选出了最值和堆里最后一个元素交换，继续
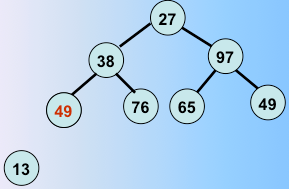
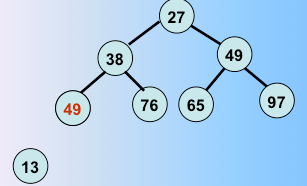
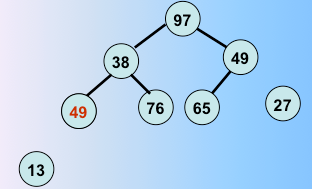
第二趟堆排序完毕，选出了次最值和剩下的元素的最后一个元素交换
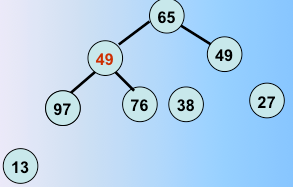
第三趟堆排序完毕，重复往复，这样进行堆调整。
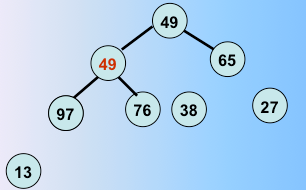
第四躺排序完毕，继续
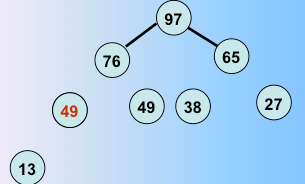
第五躺排序完毕
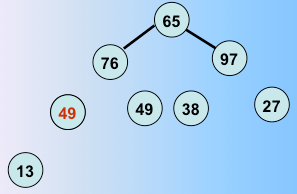
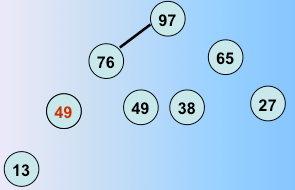
第六趟排序完毕
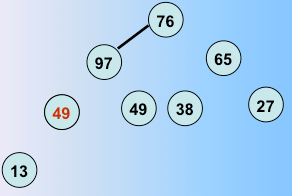
最后全部堆排序完毕
这是整个建堆，调整为小顶堆的过程，也就是递增排序。具体是自上而下调整完全二叉树里的关键字，使其成为一个大顶堆（递减排序过程）
操作过程如下：
1)初始化堆：将R[1..n]构造为堆；
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。
对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有节点都进行调整
调整堆的代码如下：
1 //堆排序的堆的调整过程 2 // 已知 H.r[s..m]中记录的关键字除 H.r[s] 之外均满足堆的特征，本函数自上而下调整 H.r[s] 的关键字，使 H.r[s..m] 成为一个大顶堆 3 void heapAdjust(int List[], int s, int length) 4 { 5 //s 为 当前子树 的 临时 堆顶，先把堆顶暂存到 temp 6 int maxTemp = s; 7 //s 结点 的 左孩子 2 * s ， 2 * s + 1是 s结点 的右孩子，这是自上而下的筛选过程，length是序列的长度 8 int sLchild = 2 * s; 9 int sRchild = 2 * s + 1; 10 //完全二叉树的叶子结点不需要调整，没有孩子 11 if (s <= length / 2) { 12 //如果 当前 结点的左孩子比当前结点记录值大，调整，大顶堆 13 if (sLchild <= length && List[sLchild] > List[maxTemp]) { 14 //更新 temp 15 maxTemp = sLchild; 16 } 17 //如果 当前 结点的右孩子比当前结点记录值大，调整，大顶堆 18 if (sRchild <= length && List[sRchild] > List[maxTemp]) { 19 maxTemp = sRchild; 20 } 21 //如果调整了就交换，否则不需要交换 22 if ( List[maxTemp] != List[s]) { 23 List[maxTemp] = List[maxTemp] + List[s]; 24 List[s] = List[maxTemp] - List[s]; 25 List[maxTemp] = List[maxTemp] - List[s]; 26 //交换完毕，防止调整之后的新的以 maxtemp 为父节点的子树不是大顶堆，再调整一次 27 heapAdjust(List, maxTemp, length); 28 } 29 } 30 }
建立堆的过程，本质还是堆调整的过程
1 //建堆,就是把待排序序列一一对应的建立成完全二叉树（从上到下，从左到右的顺序填满完全二叉树），然后建立大（小）顶堆 2 void bulidHeap(int List[], int length) 3 { 4 //明确，具有 n 个结点的完全二叉树（从左到右，从上到下），编号后，有如下关系，设 a 结点编号为 i，若 i 不是第一个结点，那么 a 结点的双亲结点的编号为[i/2] 5 //非叶节点的最大序号值为 length / 2 6 for (int i = length / 2; i >= 0; i--) { 7 //从头开始调整为大顶堆 8 heapAdjust(List, i, length); 9 } 10 }
堆排序过程
1 //堆排序过程 2 void heapSort(int List[], int length) 3 { 4 //建大顶堆 5 bulidHeap(List, length); 6 //调整过程 7 for (int i = length; i >= 1; i--) { 8 //将堆顶记录和当前未经排序子序列中最后一个记录相互交换 9 //即每次将剩余元素中的最大者list[0] 放到最后面 list[i] 10 List[i] = List[i] + List[0]; 11 List[0] = List[i] - List[0]; 12 List[i] = List[i] - List[0]; 13 //重新筛选余下的节点成为新的大顶堆 14 heapAdjust(List, 0, i - 1); 15 } 16 }
测试数据
int source[8] = {49, 38, 65, 97, 76, 13, 27, 49};
13 27 38 49 49 65 76 97 Program ended with exit code: 0
堆排序的时间复杂度和空间复杂度：
1. 对深度为 k 的堆，“筛选”所需进行的关键字比较的次数至多为 2(k-1)；
2. 对 n 个关键字，建成深度为 
的堆，所需进行的关键字比较的次数至多 4n；
3. 调整“堆顶” n-1 次，总共进行的关键字比较的次数不超过
，因此，堆排序的时间复杂度为 O(nlogn)，与简单选择排序 O(n^2) 相比时间效率提高了很多。
空间复杂度：S(n) = O(1)
堆排序是一种速度快且省空间的排序方法。相对于快速排序的最大优点：最坏时间复杂度和最好时间复杂度都是 O(n log n)，适用于记录较多的场景（记录较少就不实用），类似折半插入排序，在 T（n）=O（n log n）的排序算法中堆排序的空间复杂度最小为1。
堆排序的稳定性：不稳定排序算法
欢迎关注
dashuai的博客是终身学习践行者，大厂程序员，且专注于工作经验、学习笔记的分享和日常吐槽，包括但不限于互联网行业，附带分享一些PDF电子书，资料，帮忙内推，欢迎拍砖！
