Eigen库

MatrixXd表示任意size的矩阵，元素类型为double; VectorXd表示任意size的向量，元素类型为double.

//创建3*1的向量v，并赋值为1,2,3
VectorXd v(3);
v << 1, 2, 3;

使用固定尺寸的Matrix,Vector相比于可变尺寸的Matrix,Vector，例如Matrix3d m代替MatrixXd m(3,3)有以下优点：

运行速度更快，编译期间可实现更严格的错误检查。

Eigen中，所有的矩阵，向量都是Matrix模板类的对象，向量只是矩阵的特例，行数或者列数为1.

//便捷定义
typedef Matrix<float, 4, 4> Matrix4f;
typedef Matrix<float, 3, 1> Vector3f;
typedef Matrix<int, 1, 2> RowVector2i;

  typedef Matrix<double, Dynamic, Dynamic> MatrixXd;  //编译期未知尺寸

 Eigen中通过（）获取其元素，起始索引为0。The operator[] is also overloaded for index-based access in vectors, but keep in mind that C++ doesn't allow operator[] to take more than one argument.

 transpose()计算矩阵的转置， transpose()不支持就地转置，使用transposeInPlace()来实现就地转置。

 Array

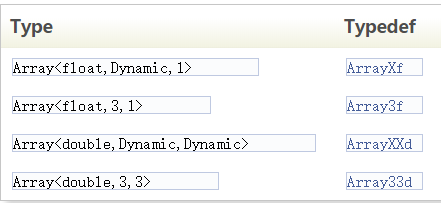
We adopt the convention that typedefs of the form ArrayNt stand for 1-dimensional arrays, where N and t are the size and the scalar type.For 2-dimensional arrays, we use typedefs of the form ArrayNNt. 

matrix和array之间可以相互进行转换，通过调用matrix的.array()函数将matrix转换为array表达式；通过调用array的.matrix()函数将array转换为matrix表达式。

Eigen中禁止一个表达式中混合使用matrix和array,但允许赋值运算符这样操作。

Eigen中为matrix提供了cwiseProduct()函数以实现逐元素相乘。

 Block Operation

matrix.row(i) 获取矩阵matrix的第i行，matrix.col(j)获取矩阵matrix的第j列。相比于使用block()性能更好。

Eigen also provides special methods for blocks that are flushed against one of the corners or sides of a matrix or array. For instance, .topLeftCorner() can be used to refer to a block in the top-left corner of a matrix.

squaredNorm() 计算2范数的平方，norm()计算2范数，lpNorm<p>()计算p范数，p设置为Infinity可计算无穷范数。

The following reductions operate on boolean values:

• all() returns true if all of the coefficients in a given Matrix or Array evaluate to true .
• any() returns true if at least one of the coefficients in a given Matrix or Array evaluates to true .
• count() returns the number of coefficients in a given Matrix or Array that evaluate to true.

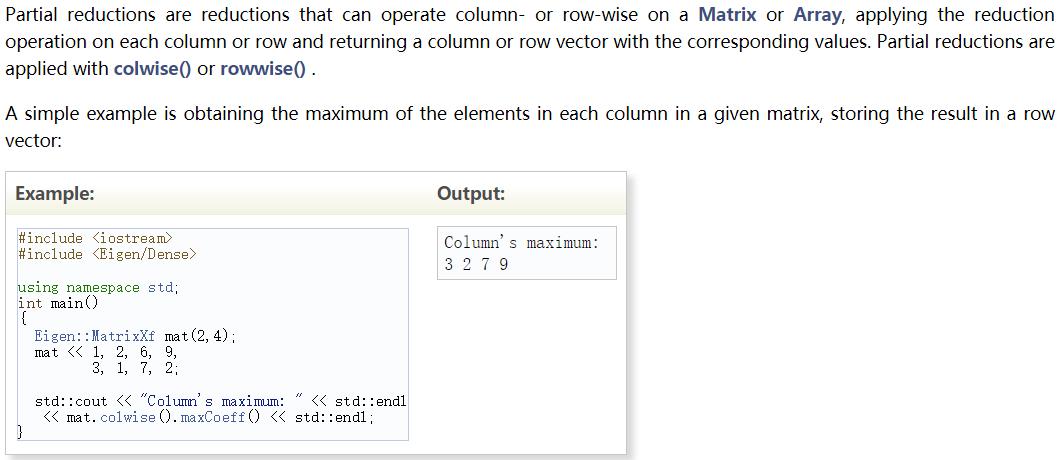
 Visitors

Visitors are useful when one wants to obtain the location of a coefficient inside a Matrix or Array. The simplest examples are maxCoeff(&x,&y) and minCoeff(&x,&y), which can be used to find the location of the greatest or smallest coefficient in a Matrix or Array.

The arguments passed to a visitor are pointers to the variables where the row and column position are to be stored. These variables should be of type Index 

 matrix.data()函数返回一个指向矩阵内存地址的指针。Eigen中矩阵默认以column-major存储元素值。