前序遍历和中序遍历唯一确定一颗二叉树

---恢复内容开始---

问题描述

如果给出了遍历二叉树的前序序列和中序序列，则可以构造出唯一的一颗二叉树。

基本要求

已知一棵二叉树的前序序列和中序序列，试设计完成下列任务的一个算法：

（1）.构造一颗二叉树

（2）.证明构造正确（即分拨儿以前序和中序遍历该树，将得到的结果

与给出的序列进行比较）

（3）.对该二叉树进行后序遍历，输出后序遍历序列

（4）.用凹入法输出该二叉树

测试数据

前序序列为ABDEGCFHIJ，中序序列为DBGEAHFIJC                                                                             

代码思路

1.确定树的根节点,树根是当前树中所有元素在前序遍历中最先出现的元素。

2.求解树的子树,找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空；若根节点左边和右边都为空，则根节点已经为叶子节点。

3.递归求解树,将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。

源代码

/*
1.确定树的根节点,树根是当前树中所有元素在前序遍历中最先出现的元素。
2.求解树的子树,找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空；若根节点左边和右边都为空，则根节点已经为叶子节点。
3.递归求解树,将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。
*/

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

const int maxint = 10000;
char ch1[maxint], ch2[maxint]; //前序序列，中序序列
int length; //二叉树结点的个数
struct tree {
    char name;
    struct tree *leftchild;
    struct tree *rightchild;
};

//访问函数
void vis(char name) {
    cout << name;
}

//初始化
void init(struct tree **root){
    *root = (struct tree *)malloc(sizeof(struct tree));
    (*root)->leftchild = NULL;
    (*root)->rightchild = NULL;
}

//创建左子树
struct tree *build_ltree(struct tree *h,char name) {
    struct tree *p, *t;
    if (h == NULL) return NULL;
    t = h->leftchild;
    p= (struct tree*)malloc(sizeof(struct tree));
    p->name = name;
    p->leftchild = t;
    p->rightchild = NULL;
    h->leftchild = p;
    return h->leftchild;
}

//创建右子树
struct tree *build_rtree(struct tree *h, char name) {
    struct tree *p, *t;
    if (h == NULL) return NULL;
    t = h->rightchild;
    p = (struct tree*)malloc(sizeof(struct tree));
    p->name = name;
    p->leftchild = NULL;
    p->rightchild = t;
    h->rightchild = p;
    return h->rightchild;
}

//凹入法打印二叉树
void print_tree(struct tree *t, int n) {
    if (t == NULL) return;
    print_tree(t->rightchild, n + 1);
    for (int i = 0; i < n - 1; i++) cout << "      ";
    if (n > 0) {
        cout<<"***";
        cout << t->name << endl;
    }
    print_tree(t->leftchild, n + 1);
}

//前序遍历
void preorder(struct tree *t, void vis(char name)) {
    if (t != NULL) {
        vis(t->name);
        preorder(t->leftchild, vis);
        preorder(t->rightchild, vis);
    }
    
}

//中序遍历
void inorder(struct tree *t, void vis(char name)) {
    if (t != NULL) {
        inorder(t->leftchild, vis);
        vis(t->name);
        inorder(t->rightchild, vis);
    }
}

//后序遍历
void postorder(struct tree *t, void vis(char name)) {
    if (t != NULL) {
        postorder(t->leftchild, vis);
        postorder(t->rightchild, vis);
        vis(t->name);
    }
}


//寻找对应中序序列中和前序序列相对应的结点的位置
int bfs(char ch[],char name) {
    int i(0);
    while (ch[i] != name) ++i;
    return i;
}

//找到左子树的位置
int seek_left(int flag[], int t){
    int temp;
    temp = t;
    while (flag[temp] != 1 && temp >= 0)
        temp--;
    if (flag[temp] == 1)
        return temp;
    else return -1;
}
//找到右子树的位置
int seek_right(int flag[], int t)
{
    int temp;
    temp = t;
    while (flag[temp] != 1 && temp <= 10000)
        temp++;
    if (flag[temp] == 1)
        return temp;
    else return -1;
}

int main() {
    while (1) {
        cout << "          ***************唯一确定一颗二叉树***************" << endl;
        cout << "          *                                              *" << endl;
        cout << "          *    给定前序序列和中序序列唯一确定一颗二叉树  *" << endl;
        cout << "          *                                              *" << endl;
        cout << "          ************************************************" << endl;
        struct tree *root; //定义根节点
        init(&root);        //创建根节点
        struct tree *node_tree[maxint]; //二叉树中的结点
        int flag[maxint];   //标记数组
        int left, right;
        memset(flag, 0, sizeof flag);  //标记数组全部赋值为0
        cout << "请输入前序序列：";
        cin >> ch1;
        cout << "请输入中序序列：";
        cin >> ch2;
        length = strlen(ch1);
        char node;  //前序序列中的结点
        int num;    //中序序列中对应前序序列结点的位置
        for (int i = 0; i < length; ++i) {
            node = ch1[i];
            num = bfs(ch2, node);
            left = seek_left(flag, num);    //找到左子树位置
            right = seek_right(flag, num);  //找到右子树位置
            if (left == -1 && right == -1) {  //第一次的时候肯定会执行这个条件后面的语句
                node_tree[num] = build_ltree(root, node);
                flag[num] = 1;
            }
            else if (left != -1 && node_tree[left]->rightchild == NULL) {
                node_tree[num] = build_rtree(node_tree[left], node);
                flag[num] = 1;
            }
            else if (right != -1 && node_tree[right]->leftchild == NULL) {
                node_tree[num] = build_ltree(node_tree[right], node);
                flag[num] = 1;
            }
        }
        cout << "此二叉树的结构是:" << endl << endl;
        print_tree(root, 0);
        cout << "此二叉树的前序序列为：";
        preorder(root->leftchild, vis);
        cout << endl;
        cout << "此二叉树的中序序列为：";
        inorder(root->leftchild, vis);
        cout << endl;
        cout << "此二叉树的后序序列为：";
        postorder(root->leftchild, vis);
        cout << endl << endl << endl;
    }
    
    return 0;
}

效果图

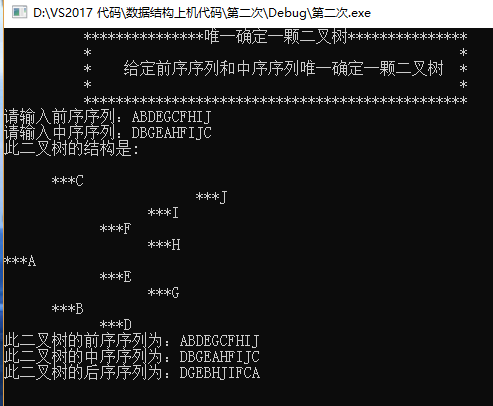
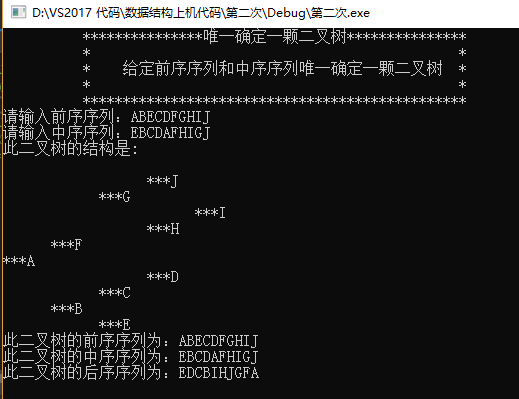
总结

断更一个月后，重新写博。呃呃呃呃呃，最近状态慢慢的调整过来了，加油吧！

下周去训练！！！

---恢复内容结束---