一、树的一些概念
树,子树,节点,叶子(终端节点),分支节点(分终端节点);
节点的度表示该节点拥有的子树个数,树的度是树内各节点度的最大值;
子节点(孩子),父节点(双亲),兄弟节点,祖先,子孙,堂兄弟,深度或高度;
森林是指若干棵或不相交的树,对于树中的每个节点,其子树的集合即为森林;
二叉树,满二叉树;
完全二叉树指一个深度为k的二叉树,它的每个节点的编号都与深度为k的满二叉树节点一一对应。例如:
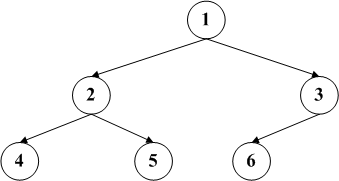
而下图则不是完全二叉树

因为它的第六个节点对应满二叉树的第七个节点。
二、BST的实现及遍历
二叉树也有链式实现和顺序实现两种方式。顺序存储极大的浪费存储空间,除非是完全二叉树或者满二叉树。但是相比于链式结构同时也能够省下申请新节点的时间。而二叉搜索树Binary Search Tree(BST)几乎是最常见的应用,BST有可能是空树,否则它应该满足如下几点要求:
1. 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值
2. 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值
3. 任意节点的左、右子树也分别为二叉查找树
4. 没有键值相等的节点。
二叉搜索树使得查找搜索的复杂度降低为O(logn)【这里指的是期望,最差情况是O(n),退化成链表,即每个节点都比它的父亲节点要大或者小】
BST的节点定义:
public class Node{
private X data;
private Node lchild;
private Node rchild;
private Node parent;
public Node (X x)
{
data = x;
lchild = rchild = parent = null;
}
public X getData()
{
return data;
}
public Node getLchild()
{
return lchild;
}
//
public Node getRchild()
{
return rchild;
}
//
public Node getParent()
{
return parent;
}
}
这里有getter方法但是没有setter方法【data可以通过构造函数赋值(但无法改变)】,这里需要思考的一个事情是是否需要在类的外部对节点进行set操作。我觉得不合适,由于BST是有序的,data若要改直接破坏搜索树的顺序,显然是不可行的;设置子节点或者父节点更是直接破坏树的结构,因此不需要,反观get操作仅仅是获取该节点的信息,放开权限可能会使用户使用更加的方便,因为parent,data等成员域均为私有属性,在类外是无法访问的。
BST类声明及成员域
class BSTree <X extends Comparable<X>>{ private Node root; /* Remaining code */ }
除了一个根节点外并没有其他的域,和链表一样的无情。这里值得注意的是泛型,这样的继承要求泛型类可比。而且只需要这一次对泛型的声明,其余类内代码拿来主义,可以直接使用泛型X,包括构造函数和成员函数,内部类等。
添加节点
public void add(X n) { Node m = new Node(n); if (root == null) { root = m; } else { Node p = root; while(p != null) { if ((p.data.compareTo(n)) > 0 && p.lchild != null) p = p.lchild; else if ((p.data.compareTo(n)) > 0 && p.lchild == null) { p.lchild = m; m.parent = p; break; } else if((p.data.compareTo(n)) <= 0 && p.rchild != null) p = p.rchild; else { p.rchild = m; m.parent = p; break; } } } }
基本思路是从根节点开始比较,如果该节点数据小于根节点那就查看其左节点,如果左节点为空直接插入,否则继续和左节点进行比较。循环如此,直到插入成功。
三序遍历
/*先序遍历*/ public void inOrder(Node t) { if (t != null) { System.out.print(t.getData()); inOrder(t.getLchild()); inOrder(t.getRchild()); } } /*中序遍历*/ public void preOrder(Node t) { if (t != null) { preOrder(t.getLchild()); System.out.print(t.getData()); preOrder(t.getRchild()); } } /*后序遍历*/ public void postOrder(Node t) { if (t != null) { postOrder(t.getLchild()); postOrder(t.getRchild()); System.out.print(t.getData()); } }
先序遍历就是先访问根节点然后访问左子树,右子树(别搞错哦);中序遍历是先访问左子树,接着根和右子树;后序遍历是先访问右子树,接着根节点和左子树。显然递归能够很好的解决这个问题,比如中序遍历,建议直接对着代码思考,很清晰直观。
查找
public Node search (X key) { Node c = root; while(c != null) { if ((c.getData().compareTo(key)) == 0) { return c; } else if ((c.getData().compareTo(key)) > 0) { c = c.lchild; } else { c = c.rchild; } } System.out.println("search failed"); return null; }
查找的思路和添加其实是一样的,不过更加简单,将判断子树是否为空改为是否和该节点数据相等即可。
遍历测试
BSTree <Integer> tree = new BSTree<>(); tree.add(3); tree.add(1); tree.add(5); tree.add(2); tree.add(4); tree.add(6); tree.inOrder(tree.getRoot()); System.out.println(); tree.preOrder(tree.getRoot()); System.out.println(); tree.postOrder(tree.getRoot()); System.out.println();
该树的结构如下所示:
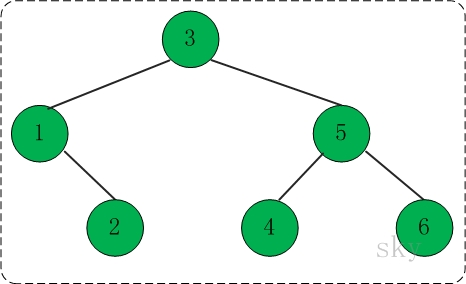
先序遍历:312546
中序遍历:123456
后序遍历:214653
此外,一个比较重要且复杂的操作即删除节点,我们首先来看删除节点有几种情况。
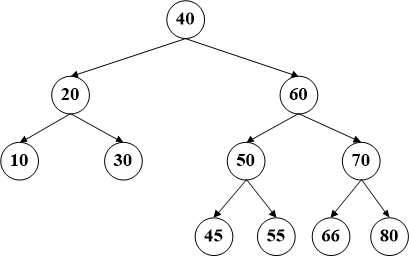
第一种,该节点没有任何子节点,那么直接进行删除即可,不需影响任何其他节点,需要注意的是删除操作要判断这个节点是其父节点的左节点还是右节点。
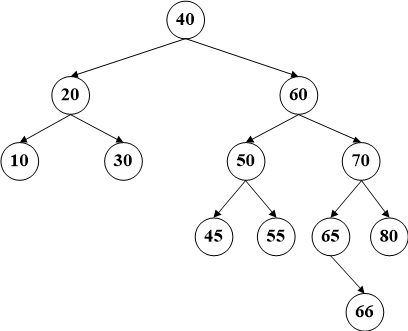

比如删除节点66,直接从左图变为右图即可。无需改变结构。
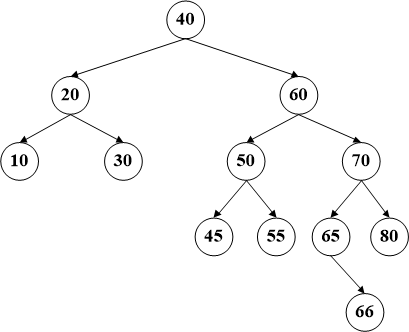
第二种,该节点只有一个子节点,此时只需将该节点的父节点和子节点直接相连即可。
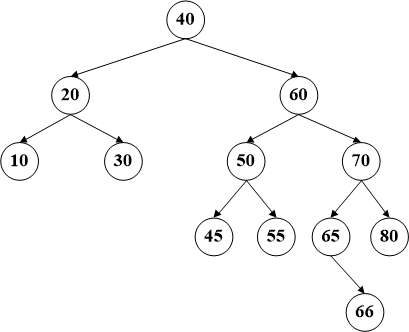
比如删除节点65,直接把70的左子节点连到66。
前两种比较简单,第三种情况是待删除节点拥有两个子树,这种情况稍微复杂,需要引入一个新的概念,即一个节点的后继节点。
一个节点后继节点的定义是在该节点的右子树上数值最小的节点,同样的,前驱节点的定义是其左子树的最大数值的节点。比如咱们例子中的节点60,它的后继节点就是65,而前驱节点是55。删除这种拥有两个子树的节点,需要首先交换该节点和其后继结点的位置(其实在代码中就是数据的交换),然后待删除的数据必将会转换为前两种情况之一,递归调用即可。
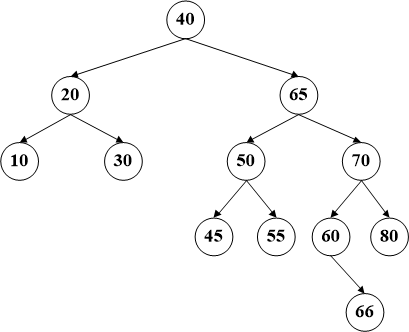
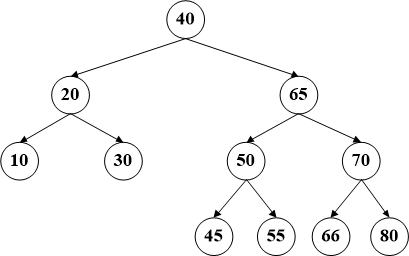
比如删除节点60,首先将该节点和其后继节点(65)交换数据【这时间是BST最危险的时刻,因为交换数据的原因已经不能保证顺序,所以务必要注意】,然后删除60所在的节点。
后继节点代码
public Node successor(Node s) { Node i = s.rchild; while (i.lchild!=null) { i = i.lchild; } return i; }
删除节点代码
public boolean remove(X r) { Node s = search(r); if(s == null) return false; if (s == root) {root = null; return true;} else if(s.lchild==null && s.rchild==null) { if (s.parent.lchild ==s) // s is leaf and left child of its parent s.parent.lchild = null; // delete s directly else s.parent.rchild = null; return true; } else if (s.rchild != null && s.lchild == null) //s只有左子节点 { if (s.parent.lchild ==s) s.parent.lchild = s.rchild; else s.parent.rchild = s.rchild; return true; } else if (s.rchild == null && s.lchild != null) //s只有右子节点 { if (s.parent.lchild ==s) s.parent.lchild = s.lchild; else s.parent.rchild = s.lchild; return true; } else //s有两个子节点 { Node successor = successor(s); X temp = successor.data; remove(temp); s.data = temp; return true; } }
测试代码
BSTree <Double> tree = new BSTree<>(); tree.add(4.0); tree.add(2.0); tree.add(6.0); tree.add(1.0); tree.add(3.0); tree.add(5.0); tree.add(4.5); tree.add(5.5); tree.add(7.0); tree.add(6.5); tree.add(6.6); tree.add(8.0); System.out.print("删除前遍历结果为"); tree.preOrder(tree.getRoot()); System.out.println(); boolean b = tree.remove(6.0); System.out.print("删除后遍历结果为"); tree.preOrder(tree.getRoot()); System.out.println();
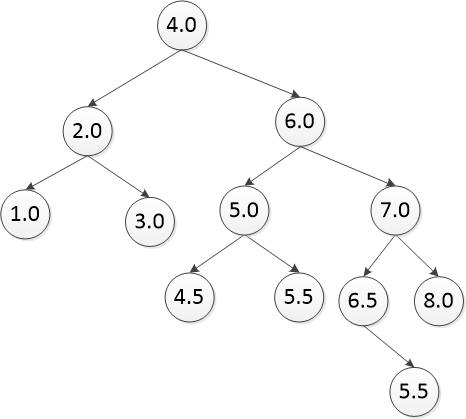
测试结果
删除前遍历结果为1.0 2.0 3.0 4.0 4.5 5.0 5.5 6.0 6.5 6.6 7.0 8.0
删除后遍历结果为1.0 2.0 3.0 4.0 4.5 5.0 5.5 6.5 6.6 7.0 8.0