数学作业

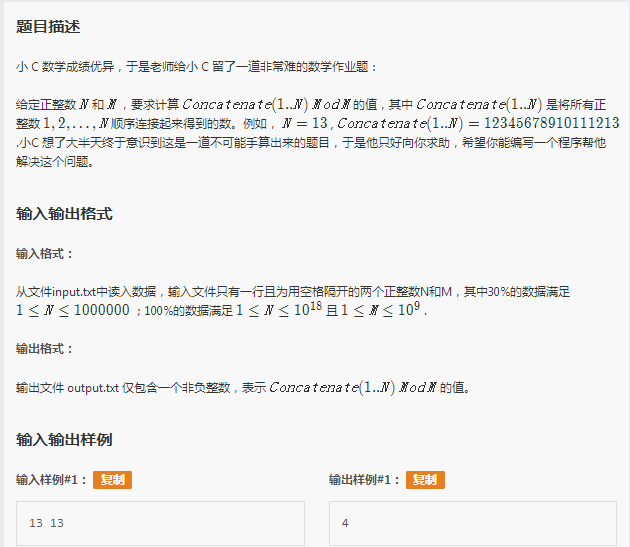
f[i]表示计算了前i位的值,f[i]=f[i-1]*10^k+i

N太大了，发现是线性常系数递推，要用矩阵来优化，就是10^n+0~10^n+9一起计算

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
ll n,mod;
struct matrix{
    int n,m; 
    ll mat[10][10];
    matrix(int n=0,int m=0):n(n),m(m){}
    void clear(){memset(mat,0,sizeof(mat));}
    void iden(){
        memset(mat,0,sizeof(mat));
        for(int i=0;i<n;i++) mat[i][i]=1;
    }
    matrix operator*(const matrix b) const{
        if(m!=b.n) exit(2);
        int p=b.m;
        matrix c(n,b.m);
        c.clear();
        for(int i=0;i<n;i++){
            for(int j=0;j<p;j++){
                for(int k=0;k<m;k++){
                    c.mat[i][j]+=mat[i][k]*b.mat[k][j];
                    c.mat[i][j]%=mod;
                } 
            }
        } 
        return c;
    }
    matrix operator^(ll p){
        matrix ret(n,n),tmp;
        ret.iden();
        for(tmp=*this;p;p>>=1,tmp=tmp*tmp){
            if(p&1) ret=ret*tmp;
        }
        return ret;
    } 
};
char buf[2007];
int main(){
    ll n,bit;
    scanf("%lld%lld",&n,&mod);
    sprintf(buf,"%lld",n);
    bit=strlen(buf);
    matrix ans(1,3);
    ans.clear();
    ans.mat[0][2]=1;
    for(int i=1;i<=bit;i++){
        ll unit=pow(10,i-1);
        matrix com(3,3);
        com.clear();
        com.mat[0][0]=unit%mod*10%mod;
        com.mat[1][0]=com.mat[1][1]=com.mat[2][0]=com.mat[2][1]=com.mat[2][2]=1;
        if(i!=bit) ans=ans*(com^(unit*9));//10^n+0~10^n+9一起计算 
        else ans=ans*(com^(n-unit+1));//到最后逐个计算 
        for(int i=0;i<3;i++) cout<<ans.mat[0][i]<<" ";
        cout<<endl; 
    }
    printf("%lld",ans.mat[0][0]);//不能加& 
    return 0;
}

return 0是c语言中的保留字,指示程序正常结束,而exit()是一个库函数,后面可以加参数；
exit(0)也可以正常退出，如果加其它的数值：1，2，....可以表示由于不同的错误原因而退出

sprintf(string,"%f",num);
string是一个字符串，num是你要的数字，这样就能将浮点数num转成字符串string了

用矩阵乘法计算斐波那契额数列：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const ll mod = 19260817;
const int N = 2;
struct Matrix{
    ll a[N][N];
    
    void clear(){
        memset(a, 0, sizeof(a));
    }
    
    Matrix operator * (const Matrix b) const{
        Matrix ret; ret.clear();
        for(int i = 0; i < N; i ++){
            for(int j = 0; j < N; j ++){
                for(int k = 0; k < N; k ++){
                    ret.a[i][j] = (ret.a[i][j] + a[i][k] * b.a[k][j]) % mod;
                }
            }
        }
        return ret;
    }
}A, B;


Matrix qpow(Matrix A, ll b){
    Matrix ret; ret.clear();
    for(int i = 0; i < N; i ++) ret.a[i][i] = 1;
    for(; b; b >>= 1, A = A * A){
        if(b & 1) ret = ret * A;
    }
    return ret;
}
ll n;
int main(){
    scanf("%lld", &n);
    A.clear(); A.a[0][0] = A.a[0][1] = A.a[1][0] = 1;
    B = qpow(A, n - 1);
    ll ans = 0;
    cout<<B.a[0][0]<<" "<<B.a[0][1]<<endl; 
    ans = (B.a[0][0] + B.a[0][1]) % mod;
    printf("%lld
", ans);
}