[POJ 3468]A Simple Problem with Integers
给定Q个数A1, ..., AQ,多次进行以下操作:
1.对区间[L, R]中的每个数都加n.
2.求某个区间[L, R]中的和.
Q ≤ 100000
Sol
如果只记录区间的和?
进行操作1的时候需要O(N)的时间去访问所有的节点.
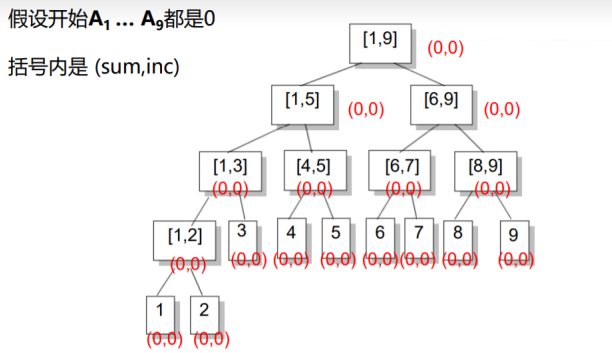
考虑多记录一个值inc,表示这个区间被整体的加了多少.
延迟更新
信息更新时,未必要真的做彻底的更新,可以只是将应该如何更新记录下来,等到真正需要查询准确信息时,才去更新 足以应付查询的部分。
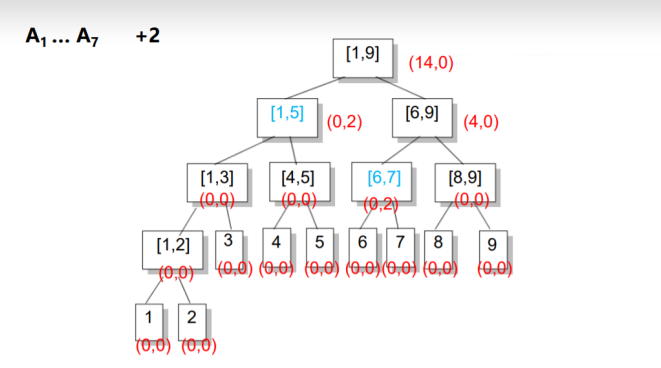
在区间增加时,如果要加的区间正好覆盖一个节点,则增加其节 点的inc值和sum值,不再往下走.
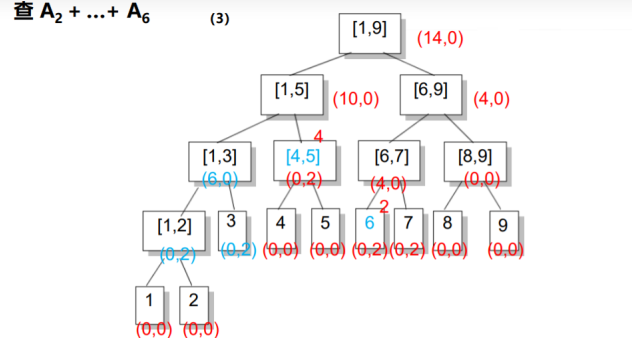
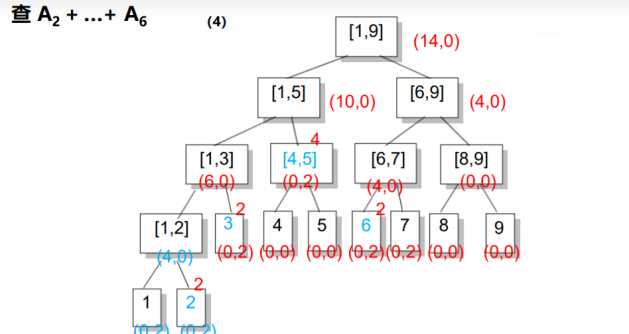
在区间询问时,还是采取正常的区间分解.
在上述两种操作中,如果我们到了区间[L, R]还要接着往下走,并且inc非0,说明子区间的信息是不对的,我们将inc传送到左儿子和右儿子上,并将inc赋成0,即完成了一次更新.


1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<iostream> 5 #include<cstring> 6 #include<string> 7 #include<cmath> 8 #include<ctime> 9 #include<set> 10 #include<vector> 11 #include<map> 12 #include<queue> 13 14 #define N 300005 15 #define M 8000005 16 17 #define ls (t*2) 18 #define rs (t*2+1) 19 #define mid ((l+r)/2) 20 21 #define mk make_pair 22 #define pb push_back 23 #define fi first 24 #define se second 25 26 using namespace std; 27 28 int i,j,m,n,p,k,lazy[N*4],sum[N*4],a[N],ans,x,c,l,r; 29 30 void build(int l,int r,int t) 31 { 32 if (l==r) sum[t]=a[l]; 33 else 34 { 35 build(l,mid,ls); 36 build(mid+1,r,rs); 37 sum[t]=sum[ls]+sum[rs]; 38 } 39 } 40 41 void down(int t,int len) //对lazy标记进行下传 42 { 43 if (!lazy[t]) return; 44 sum[ls]+=lazy[t]*(len-len/2); 45 sum[rs]+=lazy[t]*(len/2); 46 lazy[ls]+=lazy[t]; 47 lazy[rs]+=lazy[t]; 48 lazy[t]=0; 49 } 50 51 void modify(int ll,int rr,int c,int l,int r,int t) //[ll,rr]整体加上c 52 { 53 if (ll<=l&&r<=rr) 54 { 55 sum[t]+=(r-l+1)*c; //对[l,r]区间的影响就是加上了(r-l+1)*c 56 lazy[t]+=c; 57 } 58 else 59 { 60 down(t,r-l+1); 61 if (ll<=mid) modify(ll,rr,c,l,mid,ls); 62 if (rr>mid) modify(ll,rr,c,mid+1,r,rs); 63 sum[t]=sum[ls]+sum[rs]; 64 } 65 } 66 67 void ask(int ll,int rr,int l,int r,int t) //对于区间[l,r]进行询问 68 { 69 if (ll<=l&&r<=rr) ans+=sum[t]; //代表着找到了完全被包含在内的一个区间 70 else 71 { 72 down(t,r-l+1); 73 if (ll<=mid) ask(ll,rr,l,mid,ls); 74 if (rr>mid) ask(ll,rr,mid+1,r,rs); 75 } 76 } 77 78 79 int main() 80 { 81 scanf("%d%d",&n,&m); 82 for (i=1;i<=n;++i) scanf("%d",&a[i]); 83 build(1,n,1); 84 }
down:t是编号,len是区间长度
定义inc是加上的数
第34行是更新他的祖宗,因为子节点更新了,向上也要更新
叶节点的标记不下传
如果需要用到的区间在大区间中的话就将大区间的inc下传
[POJ2528]Mayor’s posters
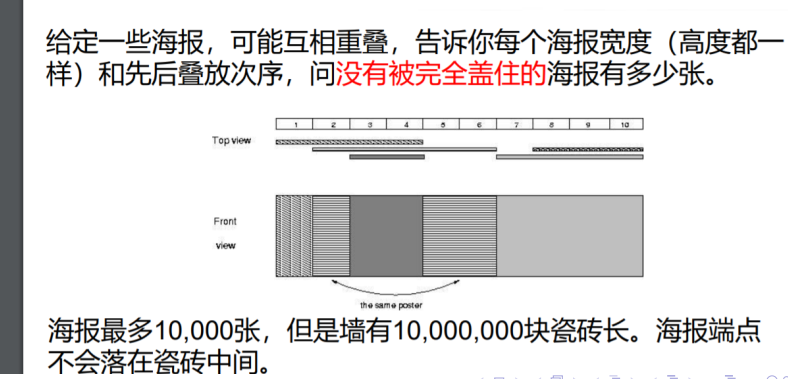
首先我们对数据进行一些处理,使得1kw的砖块数量减少.
我们将海报的所有的端点都拿出来,排序去重.
对于两个端点之间的部分,每块砖要么完全经过它们,要么完全不经过它们.
将它们当成一块砖,然后就可以把砖块数量减低到4w个了.
一共2w个端点,相邻两个端点之间生成一个砖块
算上端点在内,一共不超过4w块砖,而且两个端点中间还不一定有砖
那么我们从最底层的海报开始,一张一张往上贴.0
对于一个区间[L, R],我们记录的信息是这个区间整体被第几张海报覆盖了,初始值设为−1.
对于一张包含[L, R]的海报i,我们就只需要把[L, R]里面所有的位置都赋成i就可以了.
注意利用区间分解和延迟更新的方法.
本题中是否会有标记时间冲突的问题?并不会
只可能是后来的标记碰上先来的标记,并不可能是先来的标记碰上后来的标记
ZYB 画画
给出长度为N的序列A,
Q次操作,两种类型:
(1 x v),将Ax改成v.
(2 l r) 询问区间[l, r]中有多少段不同数。例如2 2 2 3 1 1 4,就是4段。
N, Q ≤ 100000.
Sol
线段树上的每个节点都维护三个信息:
这段区间有多少段不同的数,最右边的数,最左边的数.
合并的时候,先把段数相加,然后如果中间接上的地方相同(左儿子最右边的数=右儿子最左边的数),则段数−1.
非常简单的线段树合并操作.时间复杂度O((N + Q) log N).
树状数组
讲了RMQ问题,再来讲讲树状数组.
树状数组是一种用来求前缀和的数据结构.
记lowbit(x)为x的二进制最低位包含后面的0构成的数.
例子:lowbit(8) = 8, lowbit(6) = 2
求lowbit
记fi是i的最低位.
若i是奇数,fi = 1,否则fi = fi/2 * 2.
不觉得麻烦?lowbit(i) = i& − i.
定义
对于原始数组A,我们设一个数组C.
C[i]=a[i-lowbit(i)+1]+...+a[i]
i > 0的时候C[i]才有用.C就是树状数组.
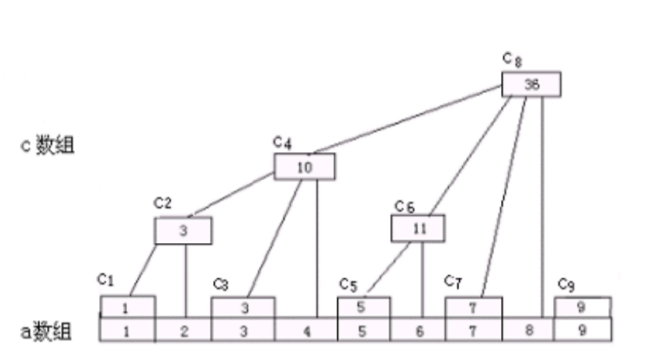
这个结构有啥用?
树状数组用于解决单个元素经常修改,而且还反复求不同的区间和的情况.
树状数组求和
树状数组只能够支持询问前缀和,不支持区间和,但是可以用前缀和求区间和.
我们先找到C[n],然后我们发现现在,下一个要找的点
是n − lowbit(n),然后我们不断的减去lowbit(n)并累加C数组.
我们可以用前缀和相减的方式来求区间和.
询问的次数和n的二进制里1的个数相同.则是O(log N).
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<iostream> 5 #include<cstring> 6 #include<string> 7 #include<cmath> 8 #include<ctime> 9 #include<set> 10 #include<vector> 11 #include<map> 12 #include<queue> 13 14 #define N 300005 15 #define M 8000005 16 17 #define ls (t<<1) 18 #define rs ((t<<1)|1) 19 #define mid ((l+r)>>1) 20 21 #define mk make_pair 22 #define pb push_back 23 #define fi first 24 #define se second 25 26 using namespace std; 27 28 int i,j,m,n,p,k,C[N],a[N],b[N]; 29 30 long long ans; 31 32 int lowbit(int x) 33 { 34 return x&-x; 35 } 36 37 void ins(int x,int y)//修改a[x]的值,a[x]+=y; 38 { 39 for (;x<=n;x+=lowbit(x)) C[x]+=y; //首先需要修改的区间是以x为右端点的,然后下一个区间是x+lowbit(x),以此类推 40 } 41 42 int ask(int x) //查询[1,x]的值 43 { 44 int ans=0; 45 for (;x;x-=lowbit(x)) ans+=C[x]; //我们询问的]是[x-lowbit(x)+1,x,然后后面一个区间是以x-lowbit(x)为右端点的,依次类推 46 return ans; 47 } 48 49 int main() 50 { 51 57 }
树状数组更新
现在我们要修改Ax的权值,考虑所有包含x这个位置的区间个数.
从C[x]开始,下一个应该是C[y = x + lowbit(x)],再下一个是C[z = y + lowbit(y)]...直到达到上限
注意到每一次更新之后,位置的最低位1都会往前提1.总复杂
度也为O(log N).
现在我们要修改Ax的权值,考虑所有包含x这个位置的区间个数.
从C[x]开始,下一个应该是C[y = x + lowbit(x)],再下一个是C[z = y + lowbit(y)]...
注意到每一次更新之后,位置的最低位1都会往前提1.总复杂度也为O(log N).
例2
求一个数组A1, A2, ..., An的逆序对数.
n ≤ 100000, |Ai| ≤ 109
Sol
我们将A1, ..., An按照大小关系变成1...n.这样数字的大小范围在[1, n]中.
维护一个数组Bi,表示现在有多少个数的大小正好是i.(离散化后)
从左往右扫描每个数,对于Ai,累加B Ai+1...Bn的和,同时将BAi加1.
时间复杂度为O(N log N)
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<iostream> 5 #include<cstring> 6 #include<string> 7 #include<cmath> 8 #include<ctime> 9 #include<set> 10 #include<vector> 11 #include<map> 12 #include<queue> 13 14 #define N 300005 15 #define M 8000005 16 17 #define ls (t<<1) 18 #define rs ((t<<1)|1) 19 #define mid ((l+r)>>1) 20 21 #define mk make_pair 22 #define pb push_back 23 #define fi first 24 #define se second 25 26 using namespace std; 27 28 int i,j,m,n,p,k,C[N],a[N],b[N]; 29 30 long long ans; 31 32 int lowbit(int x) 33 { 34 return x&-x; 35 } 36 37 void ins(int x,int y)//修改a[x]的值,a[x]+=y; 38 { 39 for (;x<=n;x+=lowbit(x)) C[x]+=y; //首先需要修改的区间是以x为右端点的,然后下一个区间是x+lowbit(x),以此类推 40 } 41 42 int ask(int x) //查询[1,x]的值 43 { 44 int ans=0; 45 for (;x;x-=lowbit(x)) ans+=C[x]; //我们询问的]是[x-lowbit(x)+1,x,然后后面一个区间是以x-lowbit(x)为右端点的,依次类推 46 return ans; 47 } 48 49 int main() 50 { 51 scanf("%d",&n); 52 for (i=1;i<=n;++i) scanf("%d",&a[i]),b[++b[0]]=a[i]; 53 sort(b+1,b+b[0]+1); b[0]=unique(b+1,b+b[0]+1)-(b+1); 54 for (i=1;i<=n;++i) a[i]=lower_bound(b+1,b+b[0]+1,a[i])-b; 55 for (i=1;i<=n;++i) ans+=(i-1)-ask(a[i]),ins(a[i],1); 56 printf("%lld ",ans); 57 }
53行去重后末尾指向空的指针减去开头的地址,得到元素的个数
LCA
在一棵有根树中,树上两点x, y的LCA指的是x, y向根方向遇到到第一个相同的点.
我们记每一个点到根的距离为deepx.
每个点的deep就是他父亲的deep+1
注意到x, y之间的路径长度就是deepx + deepy − 2 * deepLCA.
int Find_LCA(int x,int y) //求x,y的LCA { int i,k; if (deep[x]<deep[y]) swap(x,y); x=Kth(x,deep[x]-deep[y]); //把x和y先走到同一深度 if (x==y) return x; for (i=K;i>=0;--i) //注意到x到根的路径是xa1a2...aic1c2...ck //y到根的路径是 yb1b2...bic1c2...ck 我们要做的就是把x和y分别跳到a_i,b_i的位置,可以发现这段距离是相同的. if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; }
LCA的原始求法
两个点到根路径一定是前面一段不一样,后面都一样.
注意到LCA的深度一定比x, y都要小.
利用deep,把比较深的点往父亲跳一格,直到x, y跳到同一个点上.
这样做复杂度是O(len).
倍增大法
考虑一些静态的预处理操作.
像ST表一样,设fa i,j为i号点的第2^j个父亲。
自根向下处理,容易发现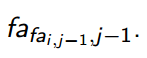
求第K个祖先
首先,倍增可以求每个点向上跳k步的点.
利用类似快速幂的想法.
每次跳2的整次幂,一共跳log次.
首先不妨假设deepx < deepy.
为了后续处理起来方便,我们先把x跳到和y一样深度的地
方.
如果x和y已经相同了,就直接退出.
否则,由于x和y到LCA的距离相同,倒着枚举步长,如果x, y的
第2^j个父亲不同,就跳上去.这样,最后两个点都会跳到
离LCA距离为1的地方,在跳一步就行了.
时间复杂度O(N log N)
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define K 18 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,fa[N][K+1],deep[N]; vector<int>v[N]; void dfs(int x) //dfs求出树的形态,然后对fa数组进行处理 { int i; for (i=1;i<=K;++i) //fa[x][i]表示的是x向父亲走2^i步走到哪一个节点 fa[x][i]=fa[fa[x][i-1]][i-1]; //x走2^i步相当于走2^(i-1)步到一个节点fa[x][i-1],再从fa[x][i-1]走2^(i-1)步 for (i=0;i<(int)v[x].size();++i) { int p=v[x][i]; if (fa[x][0]==p) continue; fa[p][0]=x; deep[p]=deep[x]+1; //再记录一下一个点到根的深度deep_x dfs(p); } } int Kth(int x,int k) //求第k个父亲,利用二进制位来处理 { for (i=K;i>=0;--i) //k可以被拆分成logN个2的整次幂 if (k&(1<<i)) x=fa[x][i]; return x; } int Find_LCA(int x,int y) //求x,y的LCA { int i,k; if (deep[x]<deep[y]) swap(x,y); x=Kth(x,deep[x]-deep[y]); //把x和y先走到同一深度 if (x==y) return x; for (i=K;i>=0;--i) //注意到x到根的路径是xa1a2...aic1c2...ck //y到根的路径是 yb1b2...bic1c2...ck 我们要做的就是把x和y分别跳到a_i,b_i的位置,可以发现这段距离是相同的. if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } int main() { scanf("%d",&n); for (i=1;i<n;++i) { int x,y; scanf("%d%d",&x,&y); v[x].pb(y); v[y].pb(x); } dfs(1); printf("%d ",Find_LCA(3,5)); }
总结
LCA能发挥很大的用处,具体可以去咨询后天教你们图论的学长.
倍增这一算法的时空复杂度分别为O(N log N) − O(log N) O(N log N).
对于求第K个祖先,利用长链剖分以及倍增算法,可以做到O(N log N) − O(1) O(N log N).
对于求LCA,利用ST表以及欧拉序可以做到O(N log N) − O(1) O(N log N)
简单的例题
有N个人,有m次操作,操作分为以下两种:
1.声明x和y是同一性别.
2.询问是否能够确定x和y是同一性别.
N, M ≤ 1000000
并查集
N个不同的元素分布在若干个互不相交集合中,需要多次进行以下3个操作:
1. 合并a,b两个元素所在的集合 Merge(a,b)
2. 查询一个元素在哪个集合
3. 查询两个元素是否属于同一集合 Query(a,b)
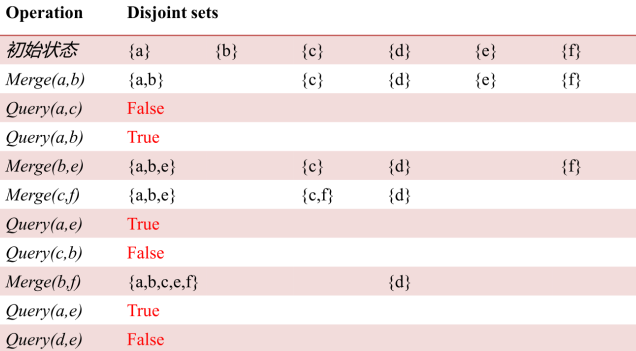
基础算法
最简单的想法:我们为每个点记录它所在的集合编号.
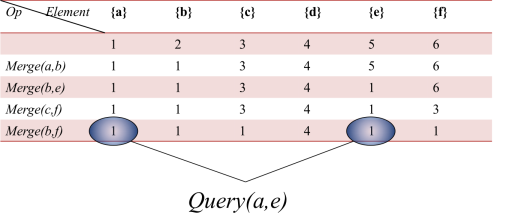
每次询问简单,但是合并的时候需要O(N)的时间,不可接受.
每次把小的并到大的上可以做到O(N log N),这样还需要记录每个集合有哪些点,非常麻烦
利用树形的结构
考虑用有根树来维护集合的形态.
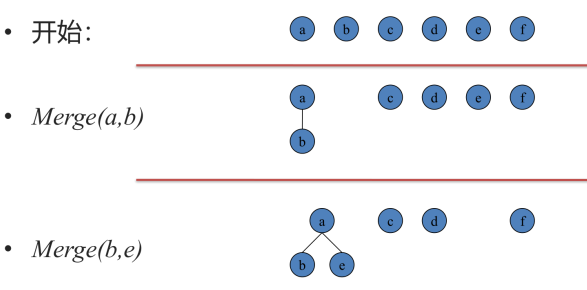

记录fai = j,表示i的父亲是j.
若fai = i,则说明i是根节点,一开始fai = i.
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,fa[N],deep[N]; int get(int x) //不加任何优化的暴力 { while (fa[x]!=x) x=fa[x]; return x; } void Merge(int x,int y) { x=get(x); y=get(y); //找到x,y所在连通块的顶点 fa[x]=y; } int Ask(int x,int y) { x=get(x); y=get(y); if (x==y) return 1;//表示连通 return 0; } int main() { scanf("%d",&n); for (i=1;i<=n;++i) fa[i]=i,deep[i]=1; Merge(2,3);//合并2,3所在的连通块 printf("%d ",Ask(2,3));//询问2,3是否在同一个连通块里 }
路径压缩
第一种优化看起来很玄学,我们在寻找一个点的顶点的时候,显然可以把这个点的父亲赋成他的顶点,也不会有什么影响.
看起来玄学,但是他的复杂度是O(N log N)的。
证明非常复杂,有兴趣的同学可以自行翻阅论文。
路径压缩的修改部分主要在Getroot部分
//路径压缩 int get(int x) { return fa[x]==x?fa[x]:fa[x]=get(fa[x]); }
按秩合并
对每个顶点,再多记录一个当前整个结构中最深的点到根的深度deepx.
注意到两个顶点合并时,如果把比较浅的点接到比较深的节点上.
如果两个点深度不同,那么新的深度是原来较深的一个.
只有当两个点深度相同时,新的深度是原来的深度+1.
注意到一个深度为x的顶点下面至少有2x个点,所以x至多为log N.
那么在暴力向上走的时候,要访问的节点至多只有log个
把两个结合起来 o(αn)α:3~4,但是一般不用
按秩合并的修改部分在于Merge,其他部分都与暴力相同
//按秩合并 void Merge(int x,int y) { x=get(x); y=get(y); 使用的是最暴力的get if (deep[x]<deep[y]) fa[x]=y; else if (deep[x]>deep[y]) fa[y]=x; else deep[x]++,fa[y]=x; }
比较
无论是时间,空间,还是代码复杂度,路径压缩都比按秩合并优秀.
值得注意的是,路径压缩中,复杂度只是N次操作的总复杂度为O(N log N)。
按秩合并每一次的复杂度都是严格O(log N)的.
两种方式可以一起用,复杂度会降的更低.
[NOI2015]程序自动分析
有N个变量,M条语句,每条语句为xi = xj,或者xi <> xj,询问这M条语句是否都有可能成立.
N ≤ 109, M ≤ 100000.
Sol
先用离散化处理出所有可能出现的变量.
可以把相同变量用并查集合并起来.
对于一条不同的语句,判断它的两个变量是否在同一个块里
[POJ1611]The Suspects
有n个学生,编号0到n − 1, 以及m个团体,0 < n ≤ 30000, 0 ≤ m ≤ 500).一个学生可以属于多个团体,也可以不属于任何团体.一个学生疑似疑似患病,则它所属
的整个团体都疑似患病。
已知0号学生疑似患病,以及每个团体都由哪些学生构成,求一共多少个学生疑似患病

Sol1
互相感染的人,应该属于同一个集合。最终问0所在的集合有几个元素.
并查集基本操作.
Sol2
考虑把每个人变成一个点.然后同一个组里的人相互之间有连边,问和0号点连通的有多少点.
边数有m * n2条,无法接受,我们给每个团体建一个点,然后所有组里的人向它连边,就把边数减到了n * m条.
用BFS找出连通块
解题关键
在Getroot和Merge时维护关键的信息.
另外一些题需要比较巧妙的建图方法.
[POJ1988]Cube Stack
有N(N ≤ 30, 000)堆方块,开始每堆都是一个方块.方块编号1N. 有两种操作:
M x y : 表示把方块x所在的堆,拿起来叠放到y所在的堆上。
C x : 问方块x下面有多少个方块。
操作最多有P(P ≤ 100, 000)次。对每次C操作,输出结果。
Sol
首先由于我们要合并的是两个堆,那么至少要维护一个fai,即代表每个方块所在的堆是哪一个.
那么,我们还需要维护一个underx,表示x这个方块下面有多少方块,初始的时候underx = 0.
那么要怎么维护underx呢?
当每次合并x, y时,我们强制将x的父亲连为y(x的根连向y的根),并将underx加上y里面数的个数.
再维护一个sizex表示x这个并查集的大小,只需要在Merge时维护,underx在Merge和Getroot时都要更新.
一个点的under之和=他所有父亲的under之和
可以用延迟更新的思想优化时间
int getroot(int a) {//路径压缩 if(parent[a]==a) return a; int t=getroot(parent[a]) under[a]+=under[parent[a]]; parent[a]=t; return parent[a]; }
程序自动分析改
有N个变量,每个变量只有0, 1两种取值.有M条语句,每条语句为xi = xj,或者xi <> xj,询问这M 条语句是否都有可能成立.
N ≤ 109, M ≤ 100000.
Sol
要注意一下只有0, 1时的区别.
把一个点拆成x, x′两个点。
如果y与x同一组,说明y与x相同.
如果y与x′一组,说明y与x不同.
那么只需要xi <> xj时i向j′连边,最后查询x和x′是否在同一组中即可