qbzt day1 上午

内容提要

模拟，贪心

---

在讲这些东西之前，我们先来了解一个东西：high level

这个东西大体上就是你做题之前要先想清楚自己要写什么，怎么写，然后再写，不要有一点写一点

1.模拟

模拟算法算是很水的算法了

模拟算法的关键就是将人类语言翻译成机器语言

更准确的说是：将一个用日常大白话语言的东西用计算机语言抽象地表达出来

所以想要良好地掌握模拟算法，就要做到以下两点：

1.优秀的读题能力;

2.优秀的代码能力;

 

例：斗地主

 

High Level

手里有n张牌

有k个规则(k<?)，每个规则可以打出一定的牌

请问最少要打出多少次牌

显然是个明显的深搜

 

void dfs(剩下多少张牌没打last，打了多少次牌ans)
{
    if(last==0)

    规则1
    规则2
    ......
    规则k
}

这个题主要还是比较考验码力

 

写码一时爽，调试火葬场

 

注意：

善用子函数

变量名清晰，自己要明白是什么东西

 

善用high level

想一想用到每个输入的地方有多少可能，需不需要特判之类的

有一个小故事

一个程序员发布了一个程序，随后他收到了5个bug

他尝试为程序写了4个补丁去修复这5个bug，他成功了

于是他现在有9个bug

QwQ

 

写长代码的要领就在于一遍写对

1.模块化（如何思考一个问题）

2.没想清楚时不动键盘，画程序逻辑图

3.写完一部分就检查一部分

 

平时做题的时候要注意习惯，尽量一遍ac

善于出数据，对拍之类的

 

贪心：

 

贪心算法的数学原理：

 

大胆猜想无需证明（划掉）

 

 

 

局部最优得到全局最优

 

在每一个状态下，都选择当前的最优解而不考虑全局的影响

 

爬山算法能较好地体现贪心的思想

 

 

 

 

可以用贪心

 

 

 

如果长成这样，就会 陷入 局部最优解

 

 

 

贪心算法要满足两个条件：1.无后效性 2.不会陷入局部最优解

 

根据贪心的数学背景我们在做贪心题目时一般有两种策略

1. 把一个问题划分成很多子问题，对每个子问题直接求最优解，然后合成一个最优解
2. 对于当前局面，搜索所有可能的临近局面，选择最优的局面进行转移

 

贪心与其说是一个算法，不如说是一种思想。

 

贪心一般都用于求解最优化问题，但是最优化问题还有很多算法，不如动规和搜索、

贪心最重要的一点就是反例。一般做题过程就是在思考规律->寻找反例->找到算法或者是重新思考的循环种度过

所以要多做题积累经验和感觉

 

贪心策略：买便宜的直到个数上限，然后再买其他的

 

首先考虑前缀和

然后这个题如果不取模是很好做的，加上取模则有两种情况

1. x-y(y<=x)
2. X+M-y(y>x)

第一种情况，y越接近0越好

第二种情况，y越接近x越好

用set+upper_bound就ok

 

经典的活动安排问题

 

按照结束点从小到大排序，遍历每一个区间，如果没有和已经选择的活动冲突就选，否则就不选

 

 

另一道经典例题：喷水装置

 

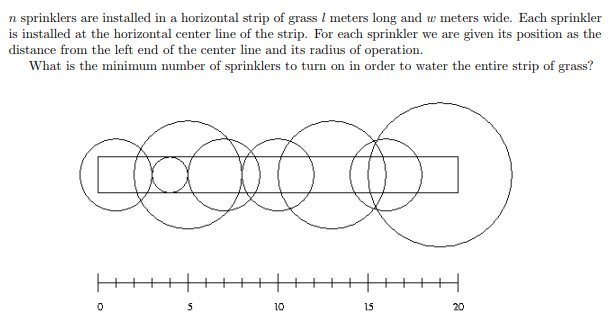
先把他按照和草坪相切的点抽象成一个数轴上面的一些线段

然后变成了线段覆盖问题

将所有的区间按左端点从小到大排序，依次处理每一个区间，每次选择覆盖点s的区间中右端点最大的一个，直到区间已经包含了这个区间内所有的点为止

 

 

另一道例题

 

 

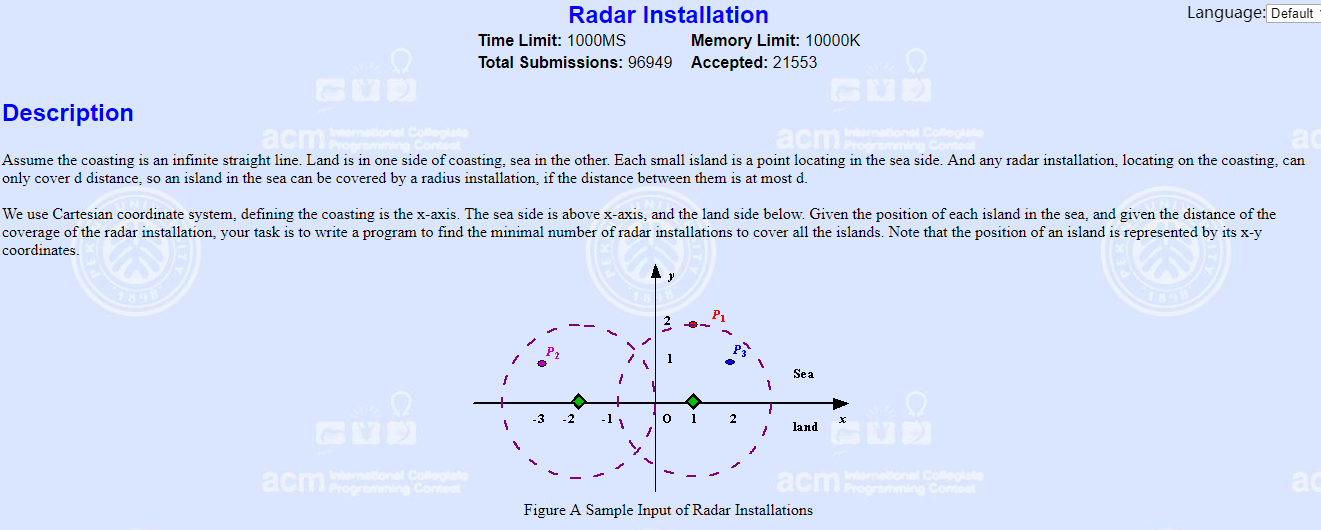
这个题可以以每个岛屿为圆心，以雷达半径为半径，和海岸线上有交点，然后跑区间选点

按照右端点从小到大排序，遍历每个区间，如果已经有点包含就转到下一个区间，否则选择最后一个点标记

 

下一道

 

首先，先把杀掉能回血的先杀了

显然杀的顺序按照消耗升序

杀完以后，不管用什么顺序杀掉剩下的怪，最后体力last是确定的

倒序来看，相当于将血药吐出来然后返还杀怪的消耗，那么显然也是按照损失体力（即血药回血量）升序，正回来即是降序。

即分为两部分，杀完能回血的按照消耗升序，剩余按血药回血量降序，然后模拟一遍判断是否合法即可

 

找到不超过它的最大的阶乘数然后减去就行了

 

其实十进制编码和转二进制编码差不多

 

 

把前k个数最大的提到最前面去，完了

 

 

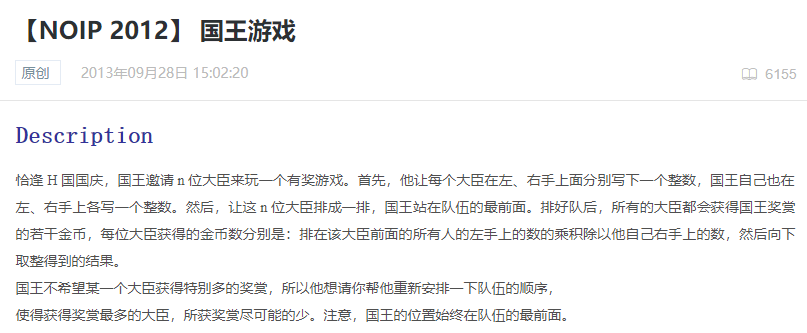
这个题就是按照左右手乘积从小到大排序就可以了

证明：考虑只交换相邻两个i，i+1，则他们之前和之后的大臣拿到的金币都不变，我们只需考虑这两个大臣本身

首先我们设这两个大臣一个为i，另一个为i+1，且l[i]*r[i]<l[i+1]*r[i+1]

交换之前i大臣拿到的金币：S/r[i]，i+1大臣拿到的金币：S*l[i]/r[i+1]，两个取max

即max(S/r[i],S*l[i]/r[i+1])

交换之后i+1大臣变成了i，他拿到的金币：S/r[i+1]

第i大臣变成了i+1大臣，他拿到的金币S*l[i+1]/r[i]，两个取max

即max(S/r[i+1],S*l[i+1]/r[i])

我们要求的是两者的最小值，即min(max(S/r[i],S*l[i]/r[i+1])，max(S/r[i+1],S*l[i+1]/r[i]) )

提出S，即S*min( max(1/r[i],l[i]/r[i+1])，max(1/r[i+1],l[i+1]/r[i]) )

然后我们显然有1/r[i]<l[i+1]/r[i]，l[i]/r[i+1]>1/r[i+1]

如果我们想要max(1/r[i+1],l[i+1]/r[i])<max(1/r[i],l[i]/r[i+1])，则必然有l[i+1]/r[i]<l[i]/r[i+1]，乘过去之后即得l[i]*r[i]>l[i+1]*r[i+1]，与题目矛盾，故乘积大的一定在前面