Stack相关 辅助栈、对顶栈 -随笔记录

一、辅助栈

*维护一个能够在O（1）内完成取序列最小值、数字入栈、数字出栈的数据结构。

对于此问题，可以通过再维护一个按照当前序列输入顺序的最小值栈（即定义栈顶的元素为此前元素的最小值，每次入栈时与栈顶比较后选择较小值入栈。）

(Acwing41)：

#include<stack>
using namespace std;
const int maxn = 1e6 + 5;


class MinStack {
public:
    stack<int> s, mins;
    
    MinStack() {
        while(!s.empty()) s.pop();
        while(!mins.empty()) mins.pop();
    }
    
    void push(int x) {
        s.push(x);
        int nowmin;
        if(!mins.empty()){
            nowmin = mins.top();
            nowmin = min(nowmin, x);
        }
        else nowmin = x;
        mins.push(nowmin);
    }
    
    void pop() {
        s.pop(), mins.pop();
    }
    
    int top() {
        return s.top();
    }
    
    int getMin() {
        return mins.top();
    }
};

二、对顶栈

*维护一个支持移动操作数据位置的序列（即在当前位置插入、删除、求此前序列最大值（or前缀和的最大值等）和移动当前操作位置等操作）

对于需要在序列中间操作的数据结构，可以考虑建立两个对口数据结构，比如对顶栈

移动操作位置只需要不断将一个栈内元素进入另一个栈中即可（插入删除入栈出栈即可，求最大值等属性可以通过辅助数组在每次元素改变时同步更新。）

ACwing128：

#include<bits/stdc++.h>
using namespace std;


int getmax[(unsigned)1e6 + 1];
int getsum[(unsigned)1e6 + 1];
int now = 0, temp;

int main(){
    ios::sync_with_stdio(false);

    memset(getmax, -0x3f, sizeof getmax);
    stack<int> left, right;
    int q;

    cin>>q;
    while(q--){
        char c;
        cin>>c;
        switch(c){
            case 'I':int x; cin>>x; left.push(x), now++;getsum[now] = getsum[now-1] + x; getmax[now] = max(getmax[now-1], getsum[now]); break;
            case 'D':if(!left.empty()) left.pop(), now--; break;
            case 'L':if(!left.empty()){right.push(left.top()); left.pop(); now--;} break;
            case 'R':if(!right.empty()){left.push(right.top()); right.pop(); now++; getsum[now] = getsum[now-1] + left.top(); getmax[now] = max(getmax[now-1], getsum[now]);} break;
            case 'Q':int k; cin>>k; cout<<getmax[k]<<endl; break;
        }
    }
    return 0;
}

三、单调栈

用于维护在特定问题中所需要的单调序列。

借由ACwing131中的情景引入问题：

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

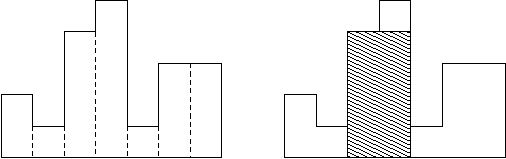
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

我们不难发现，若当前矩阵是以高度单调递增进入序列时，我们可以得到的矩形面积只需要从左到右以各自矩形高度为基础向右拓展（即乘以宽度），需要计算各个矩形向左右拓展的面积只需要不断出栈就可。

若此时进入一个高度低于栈顶的矩形，则我们可以不断令栈顶出栈，并同时计算出栈矩形的面积（以各个矩形高度为基础，宽度不断累加 --因为此时已经出栈的矩形一定高于栈中矩形，故当前可计算的大矩形面积 = （已出栈矩形数目*当前高度）

当所有高于待进栈矩形高度的矩形出栈后，我们发现虽然这些每一个出栈的矩形已经不可能再被任何一个后来进栈的矩形直接拓展利用了，但是与待进栈矩形同高的部分依然会影响后续计算

因此可以入栈一个 宽度 = 此次出栈矩形累加宽度 + 1， 高度 = 待入栈矩形高度 的矩形以保证序列的单调性。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
#define IOS ios::sync_with_stdio(false),cin.tie(0)

inline ll gcd(ll a, ll b){
    return b?gcd(b, a%b):a;
}

const int maxn = 1e6 + 5;

ll w[maxn];
ll s[maxn];
ll top;
int main(){
    IOS;
    int n;

    while(cin>>n && n){
        ll ans = 0;
        top = 0;
        
        for(int i = 0; i <= n; i++){
            ll num;

            if(i != n)
                cin>>num;
            else
                num = 0;
            if(num > s[top]) s[++top] = num, w[top] = 1;
            else{
                ll width = 0;

                while(s[top] > num){
                    width += w[top];
                    ans = max(ans, width*s[top]);
                    top--;
                }
                s[++top] = num, w[top] = width + 1;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}