包含min函数的栈、队列

题目：定义栈的数据结构，请在该类型中实现一个能够得到栈/队列的最小元素的min函数。在该栈/队列中，调用min、入栈（入队列）及出栈（出队列）函数的时间复杂度都是O(1)。

1. 包含min函数的栈

　　看到这个问题，第一反应是创建一个成员变量保存栈中当前的最小元素。每次压入一个新元素进栈时，如果该元素比当前最小的元素还要小，则更新最小元素。采用这种思路，元素入栈的时候没有问题，但出栈时如果最小的元素被弹出栈了，就无法得到下一个最小的元素。如图，元素入栈出栈过程如下，当元素3出栈时，无法确定栈中当前最小元素4。

 

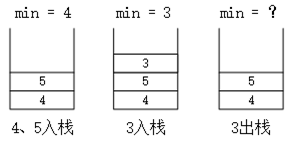
元素入栈出栈过程分析

　　分析到这里，我们发现仅仅添加一个成员变量存放最小元素时不够的，也就是当最小元素被弹出栈的时候，我们希望能够得到次小元素。因此，在压入这个最小元素之前，需要把次小元素保存起来，于是采用一个“辅助栈”保存历史最小元素。还是以上面的入栈出栈为例，多了一个辅助栈，当元素3出栈时，依然可以的到栈的当前最小元素。

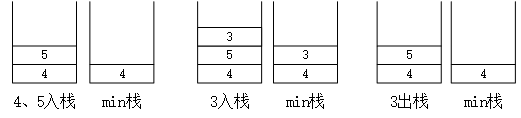
元素入栈出栈过程分析

算法的代码实现如下：

import java.util.LinkedList;
import java.util.Stack;

public class d30_MinInStack {
    public static void main(String[] args) {
        // 测试包含min函数的栈
        StackWithMin<Integer> stack = new StackWithMin<>();
        stack.push(3);
        stack.push(4);
        stack.push(2);
        stack.pop(); // 当前最小元素出栈，则minStack最小元素也要出栈
        stack.push(0);
        stack.push(-1);
        System.out.println(stack.dataStack); // [3, 4, 0, -1]
        System.out.println(stack.minStack); // [3, 0, -1]
        System.out.println(stack.min()); // -1
    }

    /*
     * 包含min函数的栈
     */
    static class StackWithMin<T extends Comparable<T>> {
        private Stack<T> dataStack; // 记录实际元素的栈
        private Stack<T> minStack; // 记录最小元素的栈

        public StackWithMin() {
            this.dataStack = new Stack<>();
            this.minStack = new Stack<>();
        }

        /*
         * 元素入栈
         */
        public void push(T data) {
            if (data == null) {
                throw new RuntimeException("cannot push null");
            }
            if (dataStack.isEmpty()) {
                dataStack.push(data);
                minStack.push(data);
            } else {
                dataStack.push(data);
                // 记录最小栈的当前最小元素
                T curMin = minStack.peek();
                // 新入栈函数小于curMin
                if (data.compareTo(curMin) < 0) {
                    minStack.push(dataStack.peek());
                }
            }
        }

        /*
         * 元素出栈
         */
        public T pop() {
            if (dataStack.isEmpty()) {
                throw new RuntimeException("dataStack is empty!");
            }
            // 如果出栈元素为dataStack栈的当前最小元素，minStack的栈顶元素出栈
            if (dataStack.peek() == minStack.peek()) {
                minStack.pop();
            }
            return dataStack.pop();
        }

        /*
         * 取栈中最小元素
         */
        public T min() {
            if (minStack.isEmpty()) {
                throw new RuntimeException("minStack is empty!");
            }
            return minStack.peek();
        }
    }
}

2. 包含min函数的队列

　　有了上面对栈的分析作为基础，实现包含min函数的队列就比较容易了。实现思路还是创建“辅助队列”，但与“辅助栈”不同的是，“辅助队列”并不是保存队列中历史最小元素。如果不是最小元素入队列，则“辅助队列”以递减的方式保存元素；如果是最小元素入队列，则“辅助队列”将其他元素出队，只保存该最小元素。具体的过程如下图所示：

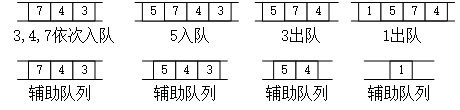
元素入队出队过程分析

算法实现代码如下：

import java.util.LinkedList;
import java.util.Stack;

public class d30_MinInStack {

    public static void main(String[] args) {
        // 测试包含min函数的队列
        QueueWithMin<Integer> queue = new QueueWithMin<>();
        queue.enqueue(3);
        queue.enqueue(4);
        queue.enqueue(7);
        System.out.println(queue.min());
        queue.enqueue(5);
        System.out.println();
        System.out.println(queue.min());
    }

    /*
     * 包含min函数的队列
     */
    public static class QueueWithMin<T extends Comparable<T>> {
        private LinkedList<T> dataQueue;
        private LinkedList<T> minQueue;

        public QueueWithMin() {
            dataQueue = new LinkedList<>();
            minQueue = new LinkedList<>();
        }

        // 元素入队
        public void enqueue(T data) {
            if (data == null) {
                throw new RuntimeException("cannot enqueue null");
            }
            dataQueue.offer(data);
            // 保证minQueue队列的元素递减
            // 若data < 队头元素，则minQueue队头元素出队
            while (!minQueue.isEmpty() && (data.compareTo(minQueue.peek()) < 0)) {
                minQueue.poll();
            }
            // 若data < 队尾元素，则minQueue队尾元素出队
           while(!minQueue.isEmpty() && (data.compareTo(minQueue.peekLast()) < 0)) {
                minQueue.poll();
            }
            minQueue.offer(data);
        }

        // 元素出队
        public T dequeue() {
            if (dataQueue.isEmpty()) {
                throw new RuntimeException("dataQueue is empty!");
            }
            // dataQueue出队元素与minQueue队头元素相等，则minQueue队头元素出队
            if (dataQueue.peek() == minQueue.peek()) {
                minQueue.poll();
            }
            return dataQueue.poll();
        }

        // 取队列最小元素
        public T min() {
            if (minQueue.isEmpty()) {
                throw new RuntimeException("minQueue is empty!");
            }
            return minQueue.peek();
        }
    }
}