题意
有两个盒子分别有m颗糖果和n颗糖果,每次移动是将一个盒子清空而把另一个盒子里得一些糖果拿到被清空的盒子,使得两个盒子至少各有一个。无法移动者输。
分析
设初始状态为(m, n),显然(1, 1)是终态。
其实对于一个状态,只与两者之和有关。按k=m+n从小到大排序,就能递推的求出每个状态是必胜还是必败。
#include<cstdio> #include<algorithm> using namespace std; const int maxn = 100 + 10; bool win[maxn][maxn]; void solve() { win[1][1] = false; for(int k = 3;k < 20;k++) { for(int n = 1;n < k;n++) { int m = k - n; win[n][m] = false; for(int i = 1;i < n;i++) if(!win[i][n-i]) win[n][m] = true; for(int i = 1;i < m;i++) if(!win[i][m-i]) win[n][m] = true; //if(n <= m && win[n][m]) printf("%d %d ", n, m); } } } int main() { solve(); for(int i = 1;i < 20;i++) for(int j = i;j <20;j++) if(win[i][j]) printf("%d %d ", i, j); }
发现规律:m,n都为奇数时先手必败;否则先手必胜。
Uva12293
题意:与Ferguson类似,不同的是,初始时两个盒子分别是(n, 1),每次选择数目较小的一个清空,并重新分配是的每个盒子中至少有一个。最先无法分配者输。
分析:
在上面的打表程序上稍做修改,
#include<cstdio> #include<algorithm> using namespace std; const int maxn = 100 + 10; bool win[maxn][maxn]; void solve() { win[1][1] = false; for(int k = 3;k <= 100;k++) { for(int n = 1;n <= k/2;n++) { int m = k - n; win[n][m] = win[m][n] = false; for(int i = 1;i < m;i++) if(!win[i][m-i]) win[n][m] = win[m][n] = true; } } } int main() { solve(); for(int i = 1;i <100;i++) if(!win[i][1]) printf("%d %d ", 1, i); }
必败态如下:
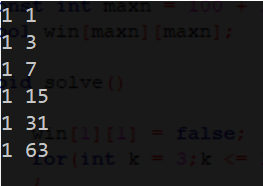
规律:(n+1)是2的整数次幂时是必败态,否则为必胜态。
判断(n+1)为2的整数次幂的方法:n&(n+1)=0.
参考链接:
1. https://blog.csdn.net/TSY_1222/article/details/83277648
2. https://blog.csdn.net/acdreamers/article/details/17020495