布隆过滤器 (Bloom Filter)是由Burton Howard Bloom于1970年提出,它是一种space efficient的概率型数据结构,用于判断一个元素是否在集合中。
看看下面几个问题:
- 字处理软件中,需要检查一个英语单词是否拼写正确
- 在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上
- 在网络爬虫里,一个网址是否被访问过
- 邮箱垃圾邮件过滤功能
以上这些场景有个共同的问题:如何查看一个东西是否在有大量数据的池子里面。
通常做法有以下几种思路:
- 数组
- 链表
- 树、平衡二叉树、Trie
- Map (红黑树)
- 哈希表
问题:
有500万条记录甚至1亿条记录?这个时候常规的数据结构的问题就凸显出来了。数组、链表、树等数据结构会存储元素的内容,一旦数据量过大,消耗的内存也会呈现线性增长,最终达到瓶颈。哈希表查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿 个垃圾 email 地址的消耗?哈希表的做法:首先,哈希函数将一个email地址映射成8字节信息指纹;考虑到哈希表存储效率通常小于50%(哈希冲突);因此消耗的内存:8 * 2 * 1亿 字节 = 1.6G 内存,普通计算机是无法提供如此大的内存。这个时候,布隆过滤器(Bloom Filter)就应运而生。
一、哈希函数

可以明显的看到,原始数据经过哈希函数的映射后称为了一个个的哈希编码,数据得到压缩。哈希函数是实现哈希表和布隆过滤器的基础。
二、布隆过滤器介绍
- 巴顿.布隆于一九七零年提出
- 一个很长的二进制向量 (位数组)
- 一系列随机函数 (哈希)
- 空间效率和查询效率高
- 不会漏判,但是有一定的误判率(哈希表是精确匹配)
三、布隆过滤器原理
布隆过滤器(Bloom Filter)的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m,哈希函数的个数为k
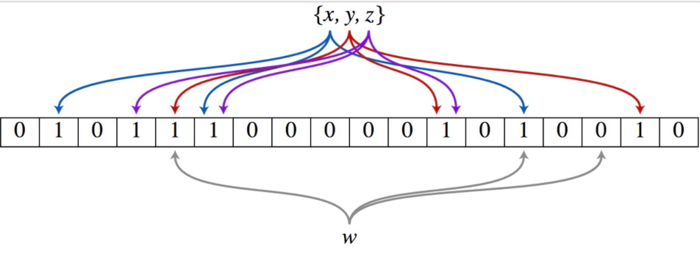
以上图为例,具体的操作流程:假设集合里面有3个元素{x, y, z},哈希函数的个数为3。首先将位数组进行初始化,将里面每个位都设置位0。对于集合里面的每一个元素,将元素依次通过3个哈希函数进行映射,每次映射都会产生一个哈希值,这个值对应位数组上面的一个点,然后将位数组对应的位置标记为1。查询W元素是否存在集合中的时候,同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1,则可以判断该元素一定不存在集合中。反之,如果3个点都为1,则该元素可能存在集合中。注意:此处不能判断该元素是否一定存在集合中,可能存在一定的误判率。可以从图中可以看到:假设某个元素通过映射对应下标为4,5,6这3个点。虽然这3个点都为1,但是很明显这3个点是不同元素经过哈希得到的位置,因此这种情况说明元素虽然不在集合中,也可能对应的都是1,这是误判率存在的原因。
添加元素
- 将要添加的元素给k个哈希函数
- 得到对应于位数组上的k个位置
- 将这k个位置设为1
查询元素
- 将要查询的元素给k个哈希函数
- 得到对应于位数组上的k个位置
- 如果k个位置有一个为0,则肯定不在集合中
- 如果k个位置全部为1,则可能在集合中
四、算法描述
一个empty bloom filter是一个有m bits的bit array,每一个bit位都初始化为0。并且定义有k个不同的hash function,每个都以uniform random distribution将元素hash到m个不同位置中的一个。在下面的介绍中n为元素数,m为布隆过滤器或哈希表的slot数,k为布隆过滤器重hash function数。
为了add一个元素,用k个hash function将它hash得到bloom filter中k个bit位,将这k个bit位置1。
为了query一个元素,即判断它是否在集合中,用k个hash function将它hash得到k个bit位。若这k bits全为1,则此元素在集合中;若其中任一位不为1,则此元素比不在集合中(因为如果在,则在add时已经把对应的k个bits位置为1)。
不允许remove元素,因为那样的话会把相应的k个bits位置为0,而其中很有可能有其他元素对应的位。因此remove会引入false negative,这是绝对不被允许的。
当k很大时,设计k个独立的hash function是不现实并且困难的。对于一个输出范围很大的hash function(例如MD5产生的128 bits数),如果不同bit位的相关性很小,则可把此输出分割为k份。或者可将k个不同的初始值(例如0,1,2, … ,k-1)结合元素,feed给一个hash function从而产生k个不同的数。
当add的元素过多时,即n/m过大时(n是元素数,m是bloom filter的bits数),会导致false positive过高,此时就需要重新组建filter,但这种情况相对少见。
五、时间和空间上的优势
当可以承受一些误报时,布隆过滤器比其它表示集合的数据结构有着很大的空间优势。例如self-balance BST, tries, hash table或者array, chain,它们中大多数至少都要存储元素本身,对于小整数需要少量的bits,对于字符串则需要任意多的bits(tries是个例外,因为对于有相同prefixes的元素可以共享存储空间);而chain结构还需要为存储指针付出额外的代价。对于一个有1%误报率和一个最优k值的布隆过滤器来说,无论元素的类型及大小,每个元素只需要9.6 bits来存储。这个优点一部分继承自array的紧凑性,一部分来源于它的概率性。如果你认为1%的误报率太高,那么对每个元素每增加4.8 bits,我们就可将误报率降低为原来的1/10。add和query的时间复杂度都为O(k),与集合中元素的多少无关,这是其他数据结构都不能完成的。
如果可能元素范围不是很大,并且大多数都在集合中,则使用确定性的bit array远远胜过使用布隆过滤器。因为bit array对于每个可能的元素空间上只需要1 bit,add和query的时间复杂度只有O(1)。注意到这样一个哈希表(bit array)只有在忽略collision并且只存储元素是否在其中的二进制信息时,才会获得空间和时间上的优势,而在此情况下,它就有效地称为了k=1的布隆过滤器。
而当考虑到collision时,对于有m个slot的bit array或者其他哈希表(即k=1的布隆过滤器),如果想要保证1%的误判率,则这个bit array只能存储m/100个元素,因而有大量的空间被浪费,同时也会使得空间复杂度急剧上升,这显然不是space efficient的。解决的方法很简单,使用k>1的布隆过滤器,即k个hash function将每个元素改为对应于k个bits,因为误判度会降低很多,并且如果参数k和m选取得好,一半的m可被置为为1,这充分说明了布隆过滤器的space efficient性。
具体算法推导和证明请参看详细链接:布隆过滤器详解