常见排序算法之python实现

1. 冒泡排序

时间复杂度为O(n^2)， 稳定的排序算法

思路：一开始比较的区间是【0，n-1】，依次比较相邻两数，哪个数大哪个数就放在后面，这样一次遍历数组后，最大的数会在数组的最后一个位置，然后比较区间从【0，n-1】缩小到了【0，n-2】，在进行一次遍历下来，第二大的数会被放在数组倒数第二的位置，依次类推。直到把范围缩小到一个数的时候，数组就有序了。

def bubbleSort(arr):
    
　　length = len(arr)
    for i in range(length-1): #趟数
        for j in range(length-i-1): #每趟元素数
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

    return arr

 2. 选择排序

时间复杂度为O(n^2)，不稳定的排序算法

思路：一开始从【0，n-1】选出一个最小值放在位置0上；第二次从【1，n-1】上选择一个最小值放在位置1上；依次类推；直到数组访问剩下一个元素时，数组有序了。

def selectionSort(arr):
    """选择排序
    """
    length = len(arr)

    for i in range(length):
        min_i = i # 最小值索引
        for j in range(i, length):
            if arr[min_i] > arr[j]:
                min_i = j

        arr[min_i], arr[i] = arr[i], arr[min_i]

    return arr

3. 插入排序*

时间复杂度为O(n^2)，稳定的排序算法

注：当数组几乎有序的情况下，时间复杂度为O(n*k)，k为最多移动的距离；当数组逆序时，时间复杂度最大为O(n^2)

思路：把n个待排序的元素看成是一个有序表和一个无序表，开始时有序表只有一个元素，无序表有n-1个元素。排序过程中每次从无序表中取出一个元素，把它的排序码依次与有序表中元素比较（后->前），将它插入有序表的适当位置，使之成为新的有序表。

def insertSort(arr):
    """插入排序
    """
    length = len(arr)

    for i in range(length-1):
        o_i = i # 有序表最后一个元素索引
        u_v = arr[o_i+1] # 无序表的元素值
        
        while o_i >= 0 and arr[o_i] > u_v:
            arr[o_i+1] = arr[o_i]
            o_i -= 1
        arr[o_i+1] = u_v # 带插入元素合适位置，+1是因为前面-1

    return arr

4. 归并排序*

时间复杂度为O(nlogn)，稳定的排序算法

思路：首先让数组每一个元素成为长度为1的有序区间；然后将两个长度为1的有序区间进行合并，生成长度为2的有序区间；然后再将两个长度为2的有序区间进行合并，生成长度为4的有序区间；依次类推，直至数组有序。1合2，2合4，4合8，8合16，……。

def mergerSort(arr):
    """归并排序

        划分成左右两部分； 两两合并，成有序数组
    """
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    # 左右划分， 生成长度为1的有序数组时开始返回
    leftArr = mergerSort(arr[:mid])
    rightArr = mergerSort(arr[mid:])
    # 两两合并
    return merger(leftArr, rightArr)

def merger(left, right):
    """合并两个有序数组，形成新的有序数组返回
    """
    res = []
    l, r = 0, 0
    while l < len(left) and r < len(right):
        if left[l] <= right[r]:
            res.append(left[l])
            l += 1
        else:
            res.append(right[r])
            r += 1

    res += left[l:]
    res += right[r:]
    return res

5. 快速排序**

时间复杂度为O(nlogn), 不稳定的排序算法

注：在数组完全无序的情况下，快排效果最好，为O(nlogn)；在有序情况下效果最差，为O(n^2)。

思路：随机排序 - 在数组中随机选择一个数，使得数组中大于它的数放在它的右边、小于等于它的数放在它的左边，然后左右两边的数递归的调用快排的过程。

快排的一次划分过程　　-　　时间复杂度为O(n)：

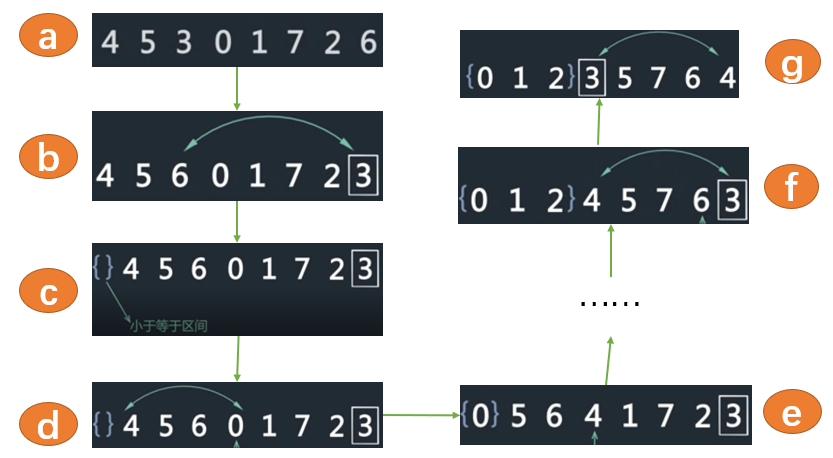
　　首先，我们随机选择数组中的一个作为划分值；然后把划分值与数组的最后一个元素进行交换，使得划分值放到数组的最后一个位置（如b）；然后我们定义一个小于等于区间，初始时，小于等于区间为空，放在数组的最左边（如c）；然后开始遍历数组，如果元素大于划分值，继续遍历下一个元素，如果元素值小于等于划分值，就让该元素与小于等于区间的下一个元素进行交换，扩增小于等于区间（如d，e）；依次执行这个过程，直到数组中只剩一个数；然后数组最后一个数（划分值）与小于等于区间的下一个数进行交换，快排的一次划分过程就结束了（如f，g）。

　　　　 

def quickSort(arr, left, right):
    """快速排序

        对left到right区间上的数组进行快排
    """
    if left >= right:
        return None

    midValue = arr[(left+right)//2] # 划分值
    l, r = left, right
    while l < r:
        while arr[l] < midValue: l += 1
        while arr[r] > midValue: r -= 1

        if l >= r: break

        arr[l], arr[r] = arr[r], arr[l]
        r -= 1
        l += 1

    if l == r:
        l += 1
        r -= 1

    if left < r: quickSort(arr, left, r)
    if right > l: quickSort(arr, l, right)

    return None

 6. 堆排序*

时间复杂度：O(nlogn)，不稳定的排序算法，常用于查找top x

思路：首先将数组【0，n-1】区间上的所有元素构建大根堆，然后将堆顶元素与数组最后一个元素进行交换，这样数组最后一个元素为最大值，作为数组有序部分存在下来；然后将数组【0，n-2】区间上的所有元素构建大根堆，然后执行堆顶元素与数组的倒数第二个元素进行交换，这样数组后两位元素分别是数组的最大值和第二大的值存在下来；然后将数组区间【0，n-3】区间构建大根堆，交换；重复以上过程直到数组有序。

def heapSort(arr):
    """堆排序
    """
    arr = buildMaxHeap(arr)

    for i in list(range(len(arr)))[::-1]:
        arr[0], arr[i] = arr[i], arr[0]
        adjustHeap(arr, 0, i) # n表示数组的大小（不是堆）

    return arr

def buildMaxHeap(arr):
    """建立大根堆

        从下向上构建
    """
    for i in list(range(len(arr)//2))[::-1]:
        adjustHeap(arr, i, len(arr))

    return arr

def adjustHeap(arr, start, size):
    """将数组[start:]调整成堆结构

        参数
        ---
            start： int
                数组起始index
            size：int
                数组大小
    """
    lChild = 2 * start + 1
    rChild = 2 * start + 2

    maxi = start

    if maxi < size//2: # 说明有孩子
        if lChild < size and arr[lChild] > arr[maxi]:
            maxi = lChild
        if rChild < size and arr[rChild] > arr[maxi]:
            maxi = rChild

        if maxi != start: # == 说明已经是最大堆了，所以这里不是
            arr[maxi], arr[start] = arr[start], arr[maxi]
            adjustHeap(arr, maxi, size)

 7. 希尔排序

时间复杂度为O(nlogn)，不稳定的排序算法

思路：希尔排序是插入排序的改良，希尔排序相比于插入排序区别在于步长是逐步调整的，也就是希尔排序在执行完指定步长的插入排序后，逐渐调整步长，直至执行步长为1的插入排序为止。一般来说，初始步长gap=length/2，然后不断以gap=gap/2减小步长，直至降为1。希尔排序的成败和步长的选取相关，步长选取越优时间复杂度越低，步长选取越劣时间复杂度越是接近O(n^2)。

def shellSort(arr):
    """希尔排序

        使用希尔增量
    """
    n = len(arr)
    gap = n // 2 # 初始化步长
    while gap >= 1:
        for i in range(gap, n):
            index = i
            while index >= gap:
                if arr[index-gap] > arr[index]:
                    arr[index-gap], arr[index] = arr[index], arr[index-gap]
                    index -= gap
                else:
                    break

        gap //= 2 # 缩减步长
    return arr