1 为什么要应用机器学习策略( Why is machine learning strategy )
当你想优化一个问题的时候,通常可以有很多尝试(比如收集更多数据,增加迭代次数,改用adam,改变网络结构,使用dropout等等),但是如果你做出了一个错误的选择,就有可能白费6个月的时间往错误的方向前进,6个月之后才意识到这方法根本不管用。如果有快速有效的方法能够判断哪些想法是靠谱的,或者提出新的想法时可以判断哪些想法是值得一试的,哪些方法是可以放心舍弃的,那就可以节省不必要的时间。接下来,ng会讲一些策略,一些分析机器学习问题的方法,分享一些他在搭建和部署大量深度学习产品时学到的经验和教训。
2 正交化( Orthogonalization )
什么是正交化,ng举了个例子,假入一台电视机有很多个按钮,1个按钮控制图像高度,1个按钮控制图像宽度,1个按钮控制旋转程度,等等,如果我们设计一个按钮,组合所有这些按钮的功能,最后想通过这个按钮来自由控制这台电视机是不可能的,我们必须用调控不同性质的按钮来控制电视机,这就是正交化,这概念就像建立线性代数空间里的基向量。
这跟机器学习有什么关系呢?首先我们机器学习想要表现好,要做到4个任务:在训练集上表现好,在验证集上表现好,在测试集上表现好,在现实世界的数据上表现好。
在训练集上表现不好,我们需要调控几个按钮去改善,比如更大的网络,使用adam算法等等;
在验证集上表现不好,我们可以调控另外几个独立的按钮去改善,比如使用正则,增大训练集等等;
在测试集上表现不好,我们可以使用更大的验证集(在验证集上表现好,在测试集上表现不好,说明对验证集过拟合了)
在现实世界的数据上表现不好,这意味着你需要回去改变你的验证集测试集,或者改变代价函数(说明测试集验证集的数据和现实数据不在同一分布,或者代价函数的设定不对)
我们要知道模型不好,到底是哪方面的问题,知道我们可以调节哪些不同的东西去尝试解决哪个问题。
ng表示他在训练神经网络的时候一般不用early stopping,因为他觉得这个按钮有点难分析,它对训练集还没拟合完全(梯度下降到一半),又对验证集进行改善,同时影响了两个任务,它没有那么正交化,就像一个旋钮同时影响宽度和高度。

3 单一实数评估指标( Single number evaluation metric )
机器学习的流程往往是你有一个想法,你尝试实现它,看看这个想法好不好,单一的实数评估指标可以快速告诉你新尝试的手段比之前的手段是好还是坏。
这样,你就可以利用验证集和单一评估指标(在验证集上观察指标好不好,以此做出调参),帮你快速迭代训练,尝试不同的想法。
比如precision和recall两个指标,不好评判,所以用综合了precision和recall的一个指标F1-score。
precision就是你预测为真且实际为真的数据占了你预测为真的数据的比例,也就是说我预测这张图片为猫,他有precision的概率是对的。
recall就是你预测为真且实际为真的数据占了实际为真的数据的比例,也就是随便拿一张猫的图片,他有recall的概率被预测为猫。
f1-score是pecision和recall的调和平均值,也就是$frac{2}{frac{1}{precision} + frac{1}{recall}}$。
再举个例子,比如你的识别猫的应用在不同地区有不同的误差,光看各地区的误差很难判别分类器的好坏,所以可以求一个平均值来作为评估指标。
4 满足和优化指标( satisficing and optimizing metrics )
要把你顾及到的所有东西组合成单实数评估指标并不容易。比如你把两个指标,准确率和运行时间,做一个线性加权求和,这样可能有点粗糙。
你可以设定在最大限度提高准确率的同时,保证满足某个运行时间要求,这样我们就称准确率为优化指标,运行时间为满足指标。这是一个合理的权衡方式。考虑实际情况,可能你的运行时间小于100ms,你的用户就不会在乎它是否更快,但是准确率是要求越高越好的。这样就可以提供一个明确的方式去选择“最好的”分类器。
假设你有N个指标,可以选择一个作为优化指标,剩下N-1都作为满足指标。
5 训练集 / 开发集 / 测试集的分布( train / dev / test distribution )
机器学习的工作流程就是,尝试很多思路,在训练集上训练不同模型,用开发集来评估不同的思路,不断迭代提高开发集的表现,最后找到一个满意的模型,用测试集进行评估。正确地设立数据集分布,可以提高效率。(开发集和验证集是一个意思)
举个例子,假设你现在有很多数据来自不同地方,你取四个地方的数据作为开发集,另外四个地方的数据作为测试集,这样的设置非常糟糕,因为它们不是来自于同一个分布。很可能你花了很多精力在开发集上调试出很好的表现,但是模型放到测试集却表现很差。所以一个建议就是把这些数据随机打乱,randomly shuffled,再放入开发集和测试集中,这样它们就来自于同一分布。
另一个例子,有个团队在做根据贷款信息判断有没有还款能力的预测,这个系统可以帮助银行判断是否批准贷款,它们的开发集是中等收入人群的贷款审批数据,训练几个月后团队突然决定要在低收入人群中做测试集,这件事对团队来说非常崩溃,这两个分布很不一样,所以最后它们花了几个月时候训练的模型,在测试的时候效果很差,相当于他们浪费了几个月的时间,现在不得不退回去重新训练。
一个guideline就是在选择开发集和测试集时,要选择能反映未来得到的数据的数据,选择能够得到好结果的重要数据。特别是开发集和测试集要来自同一分布(把你收集的数据随机散布在开发集和测试集)。
6 开发集和测试集的大小( Size of dev and test sets )
在深度学习时代,设立开发集和测试集的方针也在变化。
机器学习早期,比如说数据集在100,1000,10000的时候,一般做法是,训练测试7、3分,训练验证测试6、2、2分。
现代机器学习,我们更习惯操作大规模的数据,比如你有100万的数据,可能这样比较合理:98%用于训练,1%用于验证,1%用于测试。因为1%也有1万的数据,一般来说对于验证和测试来说已经足够了。
7 什么时候改变开发集 / 测试集 和评价指标
有时候在项目进行途中,你可能发现目标错了,这个时候你需要对数据集或评价指标做一些修改。
举个例子,你在构建猫的分类器试图找到找多很多猫的图片,假设算法A的错误率是3%,算法B的错误率是5%,你很自然地会选择A算法。
但是实际上A算法虽然准确率高,但是它会返回一些色情图片,这是公司和用户无法接收的;B算法虽然准确率低了一些,但是它不会返回色情图片;这个时候我们应该选择的是算法B,所以应该对评价指标做一些调整。可以在开发集的错误率计算公式里乘多一个权重w(除以的样本数量m要变成w的和),如果图片是色情图片w就等于10,不是色情图片w就等于1,这样当图片是色情图片时误差项就会快速变大,但是这需要在数据集中标记好哪些图片是色情图片。
总之粗略的结论就是你的评价指标无法正确评估算法时,你需要花时间定义一个新的评估指标。

这里有一个正交化的例子,就是我们是先定义评价指标,然后考虑如何优化系统来提高评价指标,这是两个独立的步骤,两个单独的按钮,不要把它们混在一起。
另一个例子是可能你在做猫的识别分类器,在你收集的高清数据集上,你的算法A错误率是3%,算法B的错误率是5%,但是应用到实际场景上你可能发现算法B效果更好,因为用户自己拍的照片可能由于模糊,角度,取景等原因,跟你训练时候的数据是不一样的。这个时候你应该修改你的验证集,测试集,让数据更能反映你实际需要处理的数据,或者修改你的评估指标,让它更符合实际应用数据的评判标准。

开发集和评价指标可以帮助我们快速迭代。ng的建议是,即使你无法定义出一个很完美的评估指标和开发集,也可以直接快速设立出来,然后驱动迭代,发现不好再回来修改。不要在没有开发集和评估指标的情况下跑太久,那样效率不高。
8 人类水平的行为( human-level performance )
机器学习的模型在学习过程中,随着时间的增加,准确率有可能超过人类的表现,但是超过人类表现后,它的增加速度就会变得很慢很慢,然后有个理论的上限阈值叫贝叶斯最优错误率,就是没办法设计出超过这个精确度的模型。所以可能当你发现你的模型到了某个程度后,特别是超越人类的表现时,准确率就无法继续上升了,对此不必太惊讶。
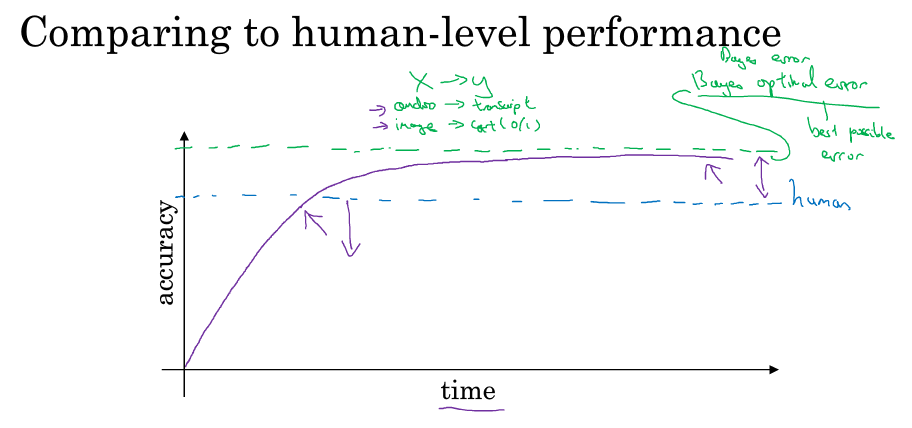
为什么超越人类水平的时候速度会慢下来呢,一个原因是人类水平的很多任务已离贝叶斯错误率不远了,所以你超越人类水平后已经没有多少空间可以上升了。第二个原因是,在你没超越人类水平之前可以通过一些工具来提高性能,但是当你超越人类水平后,这些工具就没那么好用了。
对于人类擅长做的事情,比如识别图像,识别语音或阅读语言,人类一般很擅长处理这些自然数据,只要你的机器学习算法比人类差,你就可以让人帮你标记数据,可以让人帮你分析错误,可以做更好的偏差和方差分析。总之只要你的算法比人类差,你就有这些重要策略可以改善算法,但是一旦你的算法超过人类水平,这三种策略就很难利用了。
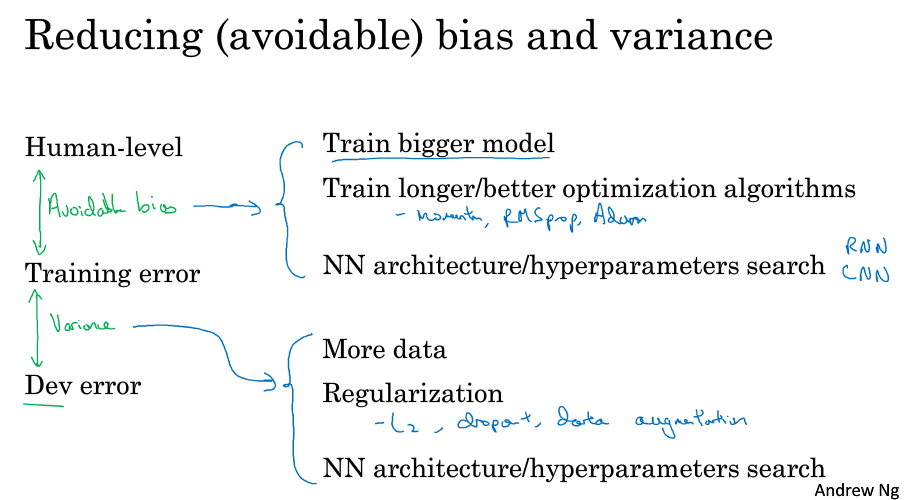
9 可避免偏差( Avoidable bias )
假设人类在识别猫的问题上错误率为1%,而你的训练集错误率为8%,开发集错误率为10%,这个时候通常会选择减少偏差,减少训练集的误差,通过扩大神经网络或者跑久一点梯度下降,因为训练集上8%的错误率和人类的1%比相差有点大。
但是如果人类在这个问题上错误率为7.5%,而你在数据集上的错误率不变,这个时候应该选择减少方差,因为训练集的误差已经很接近人类了,这个时候要减少开发集的错误率,比如利用正则或者搜集更多数据,让它接近训练集的错误率。
在这里(以及后面的阐述),我们用人类的错误率代替贝叶斯错误率,这还是挺合理的,因为人类实际上是很擅长视觉任务的,人类能达到的水平和贝叶斯错误相差不远。
ng把训练集和人类之间的错误率差距称为可避免偏差,训练集和开发集之间的错误率差距就当作方差。

10 理解人类水平的表现( Understanding human-level performance )
假设一个医学图像的分类,普通人的错误率为3%,普通医生的错误率为1%,经验丰富的医生为0.7%,经验丰富的医生团队为0.5%。那么如何定义人类水平的错误率呢?
如果我们要用人类水平替代或者估计贝叶斯误差来做分析,所以当然是用最低的错误率作为人类水平的错误率。
当你要发表论文的时候,也许人类水平误差的定义可以不一样,可以是普通医生的错误率,因为如果你的模型能过超越普通医生的表现,已经具有部署价值了。
所以这个问题要视你研究的具体问题而定。
定义不同的人类水平误差可能不会造成影响,比如training error是5%,dev error是6%,那么你定义人类水平的误差不管是1%还是0.7%还是0.5%,都是可避免偏差比较大。再比如training error是1%,dev error是5%,那么你定义人类水平的误差不管是1%还是0.7%还是0.5%,都是方差比较大。这一般是你的算法离人类水平还有一段距离的情况,这个时候可以明确地通过减少偏差或减少方差来改善问题。
定义不同的人类水平误差也可能会对你的问题造成影响,比如training error是0.7%,dev error是0.8%。这个时候如果你定义人类水平是0.7%,那么可避免偏差为0,你要解决的问题就是减少方差,缩小training error和dev error;如果你定义人类水平是0.5%,那么可避免偏差大于方差,这个时候应该减小偏差。这一般是算法已经做的很好的情况下,你无法判断应该减少偏差还是减少方差,因为你很难知道最优的误差到底是多少,可能是0.7%可能是0.5%,这两种情况导致我们要解决的问题有所不同,这也是为什么当算法逼近人类水平的时候很难再有提高的一个原因。

11 超越人类水平( surpassing human-level performance )
现在如果我们在某个问题上超越了人类水平,那么此时我们就很难去估计可避免偏差了,因为已经不能用人类水平来近似贝叶斯误差了,我们也不知道贝叶斯误差是多少,那么我们就不知道可避免偏差和方差哪个大哪个小,不知道要优化哪个问题。这时我们依然可以继续进步,只是原来可以指明方向的工具现在就没那么好用了,就比如那个根据可避免偏差和方差来改善问题的策略已经很难利用了。
现在机器学习有很多应用已经超越人类水平了,比如在线广告,产品推荐,贷款预测。这些问题有一些特点:结构化数据,非感知的(在自然感知上的问题机器比较难超越人类),用了大量的数据(这些算法看到的数据都比人类看到的多很多)。这些特点的问题比较容易得到超越人类水平的算法。
要达到超越人类的表现是很不容易的事,但有了足够多的数据,已经有很多深度学习系统在单一监督学习问题上超越了人类水平。
1.12 改善你的模型的表现( Improving your model performance )
简单总结下,就是通过观察可避免偏差和方差哪个大,然后用对应的按钮(策略)来改善你的模型。