题目分享Q

题意：给出一个N个点的树,找出一个点来,以这个点为根的树时,所有点的深度之和最大

分析：这可以说是换根法的裸题吧

首先考虑对一个给定的根如何计算，这应该是最简单的那种树形dp吧甚至可能都不算dp（好像还真不算dp）

dp[i]表示i点所有孩子（包括自己）的深度之和

deep[i]表示i点的深度

dp[x]=sum(dp[v]) +deep[x]    v|v是x的子节点

用一遍dfs即可搞定dp[1]-dp[n]

当然这里用谁为根都可以，用1就行

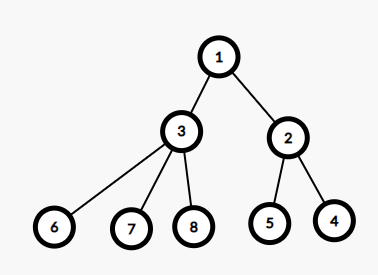
 比如我们现在已经处理出dp[1]-dp[n]的值

因为如果我们用2做根的时候,虽然发现所有人的dp值都改变了（每个人深度都改变了），这与我们之前学习的换根法可能会有一点区别

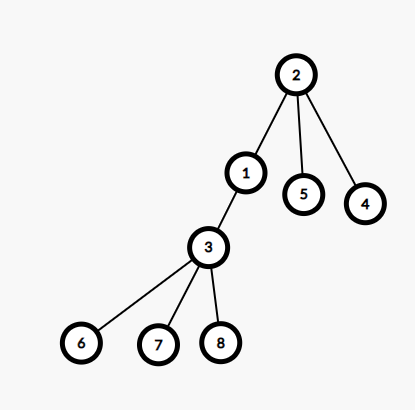
 但能发现的是，我们当前根节点的儿子想上位所需要改变的东西（dp值）其实O(1)就可以解决，或者说有规律可言，所以我们可以用换根法

那么怎么改变？或者说有什么规律？

首先要先记住一点的还是那个状态转移方程      dp[x]=sum(dp[v]) +deep[x]    v|v是x的子节点

再考虑这里面中每一项都怎么变的

就拿原来根是1换成2来说

首先，1除了2以外的子树的所有节点包括1在内（1,3,6,7,8），深度都+1

而2的子树包括2在内（2,3,5），深度都-1

然后好像就没啥别的变化了

那么再看dp值是怎么变的

首先dp[1]的值要先减去dp[2]的值，得到1除了2以外的子树包括1在内的深度之和，而得到这个之和dp[1]还要加上这些节点的个数，因为每个节点的深度都加一嘛

用son[i]表示i的子节点个数（包括自己）

也就是说dp[1]=dp[1]-dp[2]+(son[1]-son[2])(这是1除了子树2以外的节点数目)

而dp[2]是要先减去节点个数，再加上当前1的dp值（dp[1]修改后的值），因为此时1已经是2的儿子了

dp[2]=dp[2]-son[2]+dp[1]

注意这里是有先后顺序的

当然我们在第一遍dfs的时候要多算一遍son[i]

还有一点细节

在我们换根的时候要记得dfs完这个子树要还原成原来的样子再dfs下一个子树，而我们在dfs子树的时候其实与根节点是没有关系的，dfs只能往下搜嘛

也就是说我们在交换1和2的时候dp[1]的值不需要修改，所以我直接把dp[1]的式子带入到dp[2]的式子里就行了，也就是

dp[2]=dp[2]-son[2]+dp[1]-dp[2]+son[1]=dp[1]+son[1]-son[2]*2

最后把以所有点为根的结果取个最值就行了

代码：

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

#define ll long long

const int maxn=1e6+1;

struct Node
{
    int to,next;
}e[maxn<<1];
int head[maxn];
ll dp[maxn];
int son[maxn];
int cnt,k,n;
ll maxans;

void add(int x,int y)
{
    e[++cnt].to=y;
    e[cnt].next=head[x];
    head[x]=cnt;
}

void dfs1(int x,int fa,int now)
{
    dp[x]=(ll)now,son[x]=1;
    for(int i=head[x];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v!=fa)
        {
            dfs1(v,x,now+1);
            dp[x]+=dp[v];
            son[x]+=son[v];
        }
    }
}

void dfs2(int x,int fa)
{
    if(dp[x]>maxans||dp[x]==maxans&&x<k) k=x,maxans=dp[x];
    for(int i=head[x];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v!=fa)
        {
            ll now=dp[x]-dp[v]+(ll)son[x]-(ll)son[v]*2;//这里是为了方便还原，下面用的+=和-=
            int nowv=son[v];
            son[v]=son[x];
            dp[v]+=now;
            dfs2(v,x);
            dp[v]-=now;
            son[v]=nowv;
        }
    }
}

int main()
{
    int n,x,y;
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    dfs1(1,-1,1);dfs2(1,-1);
    printf("%d",k);
    return 0;
}