题意:现在两个人做游戏,每个人刚开始都是数字1,谁赢了就能乘以k^2,输的乘以k(k可以是任意整数,每次不一定相同)现在给你最终这两个人的得分,让你判断是否有这个可能,有可能的话Yes,否则No。
分析:这题其实想起来也很好想,写起来也很好写,主要还是分享一下处理类似细节的方法
首先还是先回归到这个题,显然如果满足条件,首先a*b=x³,a,b分别为这两人的最终得分,然后考虑一下还需满足什么性质
我们还是从只有一轮开始考虑,a=k²,b=k,a*b=k³,这里就很容易想到几种判断方法,比如a=b²,或者a/b=k=³√a*b,等等,只要这个判断方法只与a与b有关就行(废话)
再考虑两轮的情况,a=k1²*k2²,b=k1*k2,这看上去上面两种方法都会判断为yes,答案也真就是yes
但如果a=k1²*k2,b=k1*k2²,这样看上去好像两种方法都会判断为no,而正确结果应该是yes,
那么到底应该怎么做呢?
不难发现的是,无论这两个数怎么变换,a=k1^c1*k2^c2*k3^c3……*kn^cn,b=a=k1^d1*k2^d2*k3^d3……*kn^dn,其中ci+di=3
a和b都是在k1*k2*k3*……*kn到k1²*k2²*k3²*……*kn²之间浮动,而且他们显然都满足一个性质即能整除k1*k2*……*kn=³√a*b、*
那么我们大胆假设,满足a*b=x³且a,b能整除³√a*b的数一定满足条件吗
/* 这对于k1,k2,……,kn互质来说一定是显然成立的,但如果不一定互质,那可能很多人就有些犹豫或者迷糊
既然这样,那么我们就把不互质的转化成互质的
很容易想到,每一个ki^ci或di都会变成p1^e1^ci*p2^e2^ci*……*pn^en^ci,当然这里的pi是质数,而ei则是非负整数,当然上面的结论也要搬过来,e1*ci+e1*di=3(这里前面一个e1是指a中ki的系数,后一个是b中的)
a=p1^f1*p2^f2*p3^f3……*pn^fn,b=p1^g1*p2^g2*p3^g3……*pn^gn,这里的fi=每个ki的ei与ci的乘积,(写起来变量名太容易冲突了,理解就行)
当然,联系上面的结论,很容易得到fi+gi=3h,
说了这么多,可能很多人都忘了我们要干啥了,现在我们把不互质的转化成了互质的,显然这里面fi的最小值还是h,所以也就得证了
*/ 当然,我这上面证明的有点乱,但其实真的很好证,当然如果不会证也没关系,而且今天我主要分享的也不是这个,这个/* */的大可以不看
先再梳理一下,我们只需要保证a*b=x³且a%x==0&&b%x==0即可
那么如何判断a*b是不是立方数呢?
当然我们可以二分,不过cmath里面pow这个函数给了我们方便
有些人可能只知道p=pow(q,2),不知道p=pow(q,1/2)
对,这其实就与sqrt等价了
那么这个题我求出了pow(a*b,1/3)然后呢?
只需要判断这个数是不是整数即可,那这又咋判断呢?
首先我们要知道的是double是有精度的,一般为6-7位,具体是什么意思呢?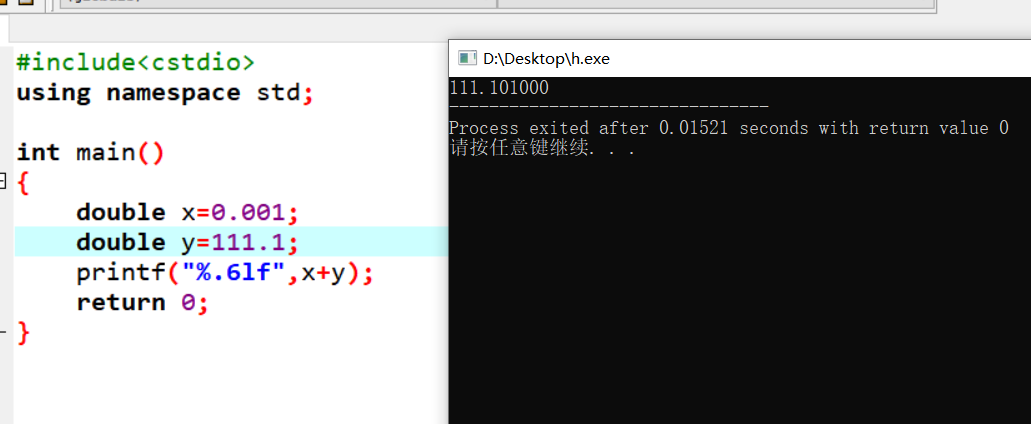
这显然没啥问题
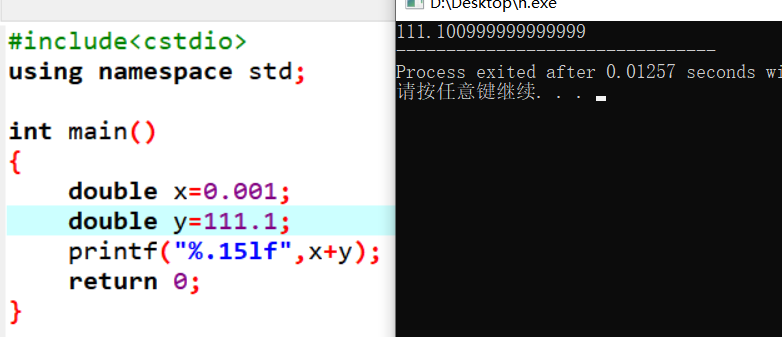
这问题就出来了,而且这不光是在小数的时候,整数运算虽然问题不是很大,但也要小心
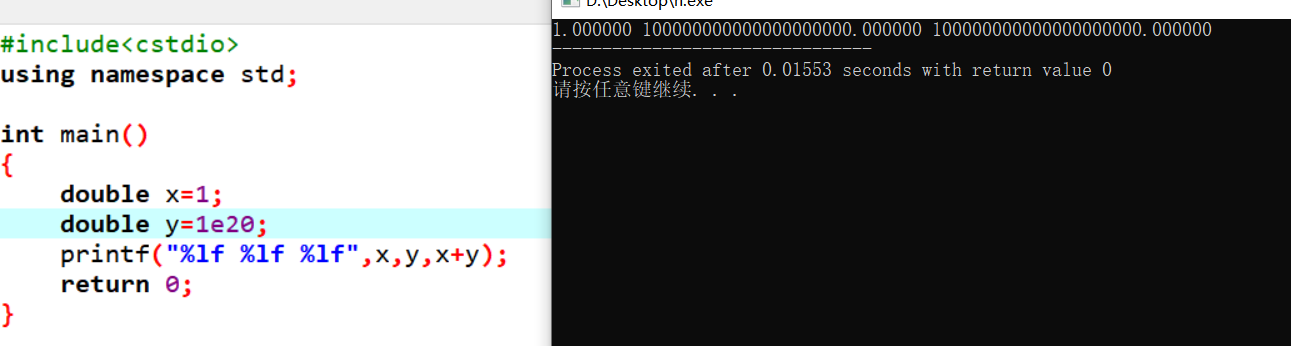
当然,不需要太过紧张,首先我这里y是1e20,都超过longlong的范围了,而上面的999999在你保留6,7位的时候也是完全没有影响的,但却有可能产生0.000001的误差
这在平日的输出结果中没有任何影响,但在判断是否相等或者将其赋值给int以求取整时便会有着灾难性的问题出现,比如
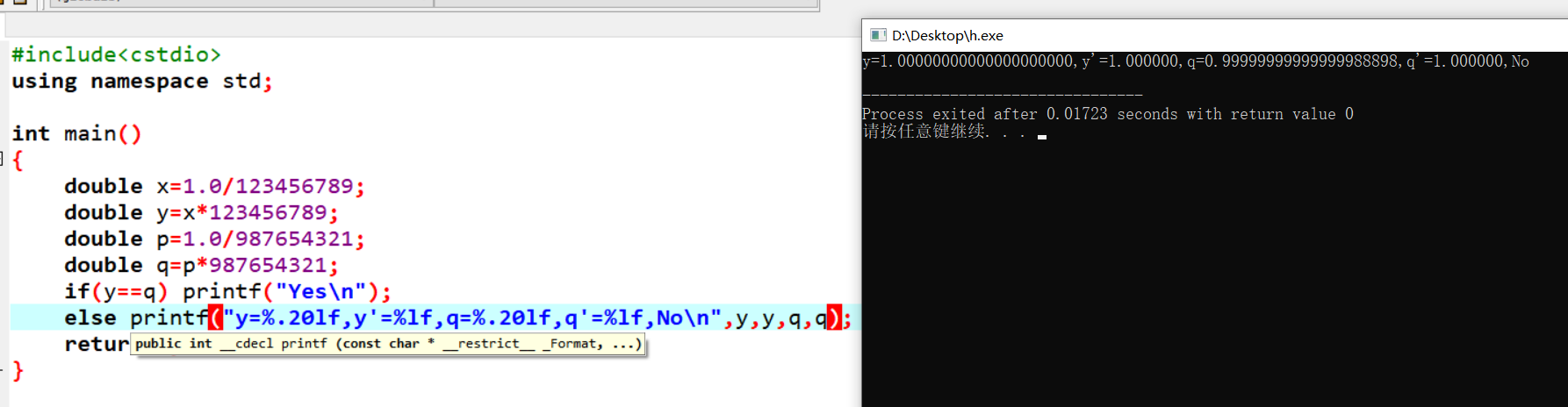
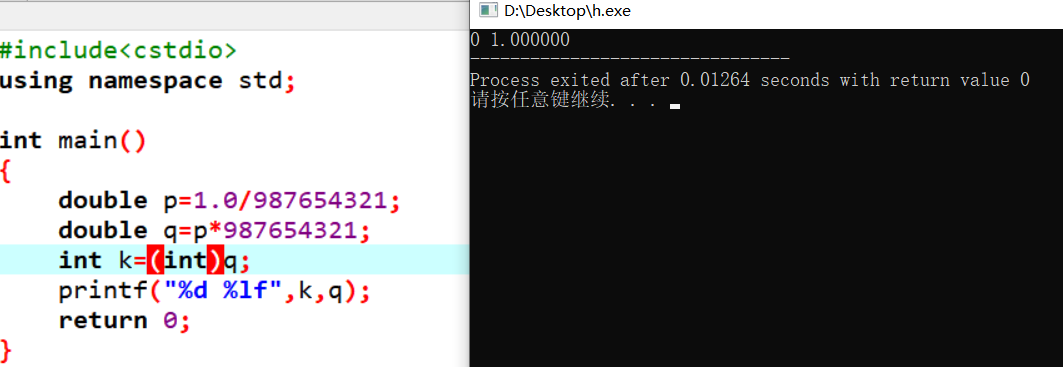
这里就需要利用我们的精度了
如果我们要表达y==q要改成abs(y-q)<=0.000001
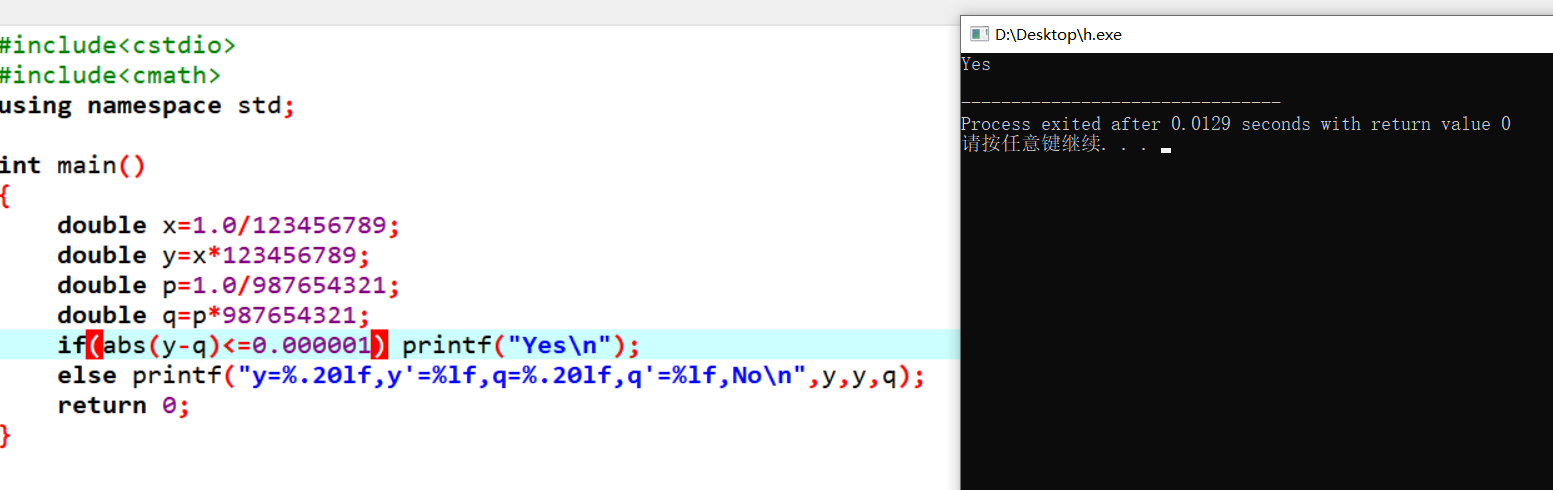
而如果我们要表达k=(int)q要改成k=(int)(q+0.000001)
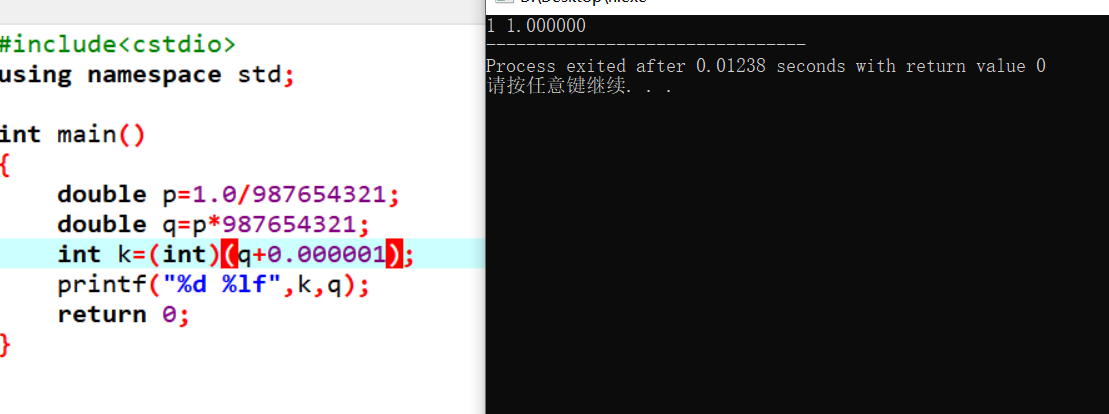
所以又说了这么多,再回到开始的问题,我们需要判断这个数是否是整数,那么就可以用abs(x-(int)(x+0.000001))<=0.000001来判断
还有几点要注意的,
1. a*b可能爆int
2. pow里面后面那个要写1.0/3,如果写1/3的话就成0了(1/3是int类型的)
3. Yes还是YES还是yes,No还是NO还是no看清楚
代码:
#include<cstdio> #include<cmath> using namespace std; #define ll long long const double minlf=0.000001; int pd(ll x) { double sq=pow(x,1.0/3); int sqr=(int)(sq+minlf); if(abs((double)sqr-sq)<=minlf) return sqr; else return 0; } int main() { int n,x,y; scanf("%d",&n); while(n--) { scanf("%d%d",&x,&y); int now=pd((ll)x*y); if(now&&x%now==0&&y%now==0) printf("Yes "); else printf("No "); } return 0; }