题意:给一个有n个顶点m条无向边的图,点有点权ai,边有边权wi,求每个顶点i的min(dis(i,j)*2+aj),其中dis(i,j)为i到j的最短路长度,且i可以和j相同
分析:
如果存在i->a的路径,显然i的结果可以由min(dis(a,j)*2+aj)+wi->a*2来更新,也就是ans[i]=min(ans[i],ans[a]+wi->a*2)
这已经很像dp,或者说,这已经很像dij了
那么显然,我可以把它作为边的价值为wi*2,初始dis值为ai的一个图,
而每次都想dij一样,用优先队列取出最小的ans值更新其他人
这个可能稍微有点抽象
当然也可以找一个源点0,还是图上的边权全部乘以2,0再连向1-n一条ai的点
也就是
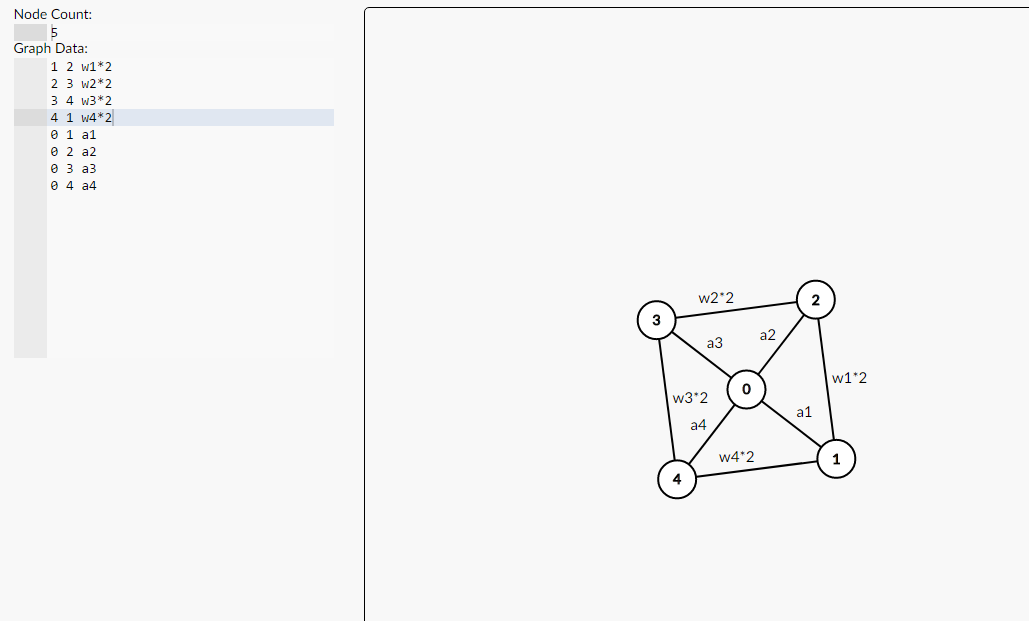
这样,也是可以的,建完图之后只需要在源点跑个最短路即可
最后直接输出dis 1-n的值
代码:
#include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; #define ll long long const int maxn=2e5+1; struct Node { int to,next; ll val; }e[maxn<<1]; struct px { int x; ll val; px(){} px(int X,ll VAL){x=X,val=VAL;} friend bool operator < (const px &x,const px &y) { return x.val>y.val; } }; int head[maxn]; bool vis[maxn]; ll dis[maxn]; int cnt,n; void add(int x,int y,ll z) { e[++cnt].to=y; e[cnt].next=head[x]; e[cnt].val=z; head[x]=cnt; } void dij() { priority_queue<px> q; for(int i=1;i<=n;i++) q.push(px(i,dis[i])); while(!q.empty()) { px now=q.top();q.pop(); if(vis[now.x]) continue; vis[now.x]=1; for(int i=head[now.x];i;i=e[i].next) { int v=e[i].to; ll nowval=now.val+e[i].val*2; if(nowval<dis[v]) dis[v]=nowval,q.push(px(v,nowval)); } } for(int i=1;i<=n;i++) printf("%lld ",dis[i]); } int main() { int m,x,y; ll z; scanf("%d%d",&n,&m); while(m--) { scanf("%d%d%lld",&x,&y,&z); add(x,y,z);add(y,x,z); } for(int i=1;i<=n;i++) scanf("%lld",&dis[i]); dij(); return 0; }