排序算法说明

排序算法说明

排序算法的基本概念

排序算法是《数据结构与算法》中最基本的算法之一。

排序是一个非常经典的问题，它以一定的顺序对一个数组（或一个列表）中的项进行重新排序（可以进行比较，例如整数，浮点数，字符串等）（增加，非递减，递减， 增加，词典等）。
有许多不同的排序算法，每个都有其自身的优点和局限性。
排序通常被用作各种计算机科学课程中的介绍性问题，以展示一系列算法思想。
在不失概性的情况下，我们假设在这个可视化中，我们将只按非递减顺序对整数进行排序，但不一定是明显的。

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

---

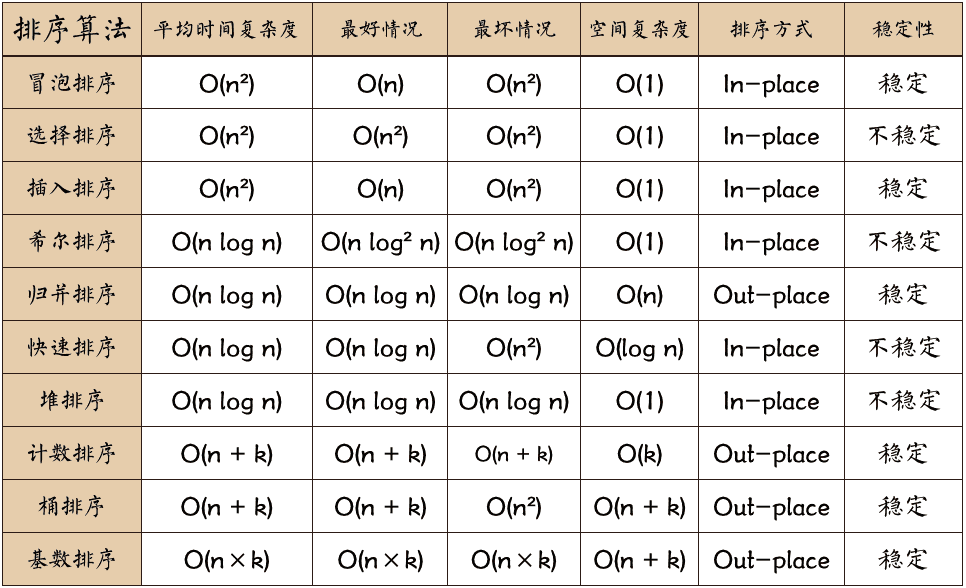
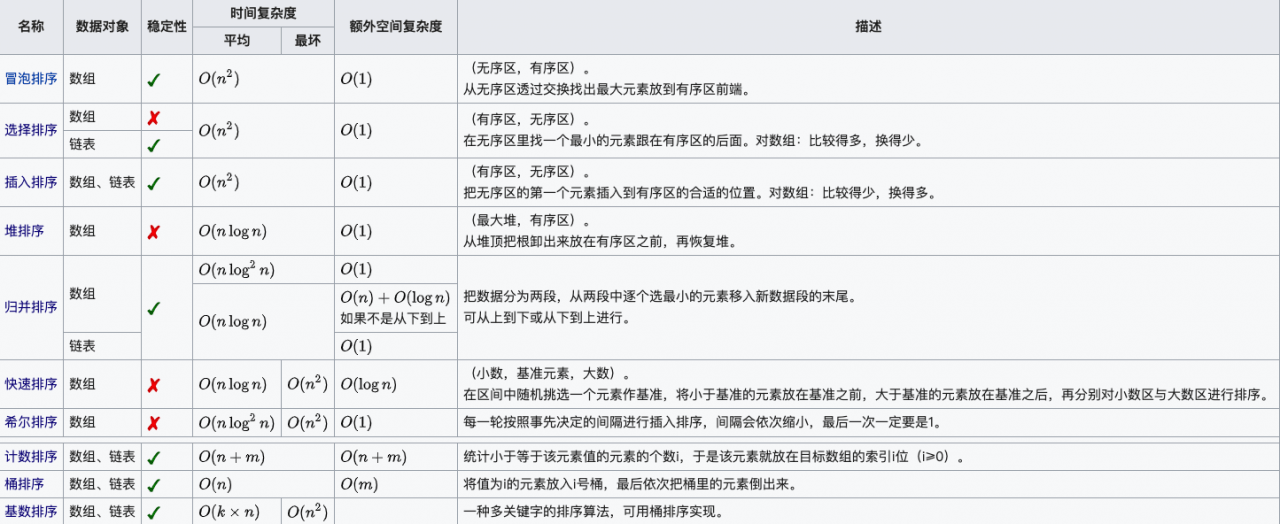
排序算法的应用

排序问题有许多有趣的算法解决方案，体现了许多计算机科学的想法：

1. 比较与非比较策略，
2. 迭代与递归实现，
3. 分而治之范式，
4. 最佳/最差/平均情况时间复杂性分析，
5. 随机算法等

当（整数）数组 A 排序时，涉及 A 的许多问题变得简单（或更容易）：

1. 在数组 A 中搜索特定值 v，
2. 查找（静态）数组 A 中的最小/最大/第 k 个最小/最大值，
3. 测试唯一性并删除数组 A 中的重复项，
4. 计算特定值 v 在数组 A 中出现多少次，
5. 设置数组 A 和另一个排序数组 B 之间的交集/联合，
6. 寻找一个目标对 x∈A 和 y∈A，使得 x + y 等于目标 z 等。

排序算法：关于时间复杂度

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

• • n：数据规模
  • k："桶"的个数
  • In-place：占用常数内存，不占用额外内存
  • Out-place：占用额外内存
  • 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同