最小生成树
问题提出:
要在n个城市间建立通信联络网,城市间的通信线路造价不同,希望找到一种方案使得建立该通信网所需花费的总代价最小。
问题分析:
n个城市间,最多可设置n(n-1)/2条线路; n个城市间建立通信网,至少需n-1条线路;
问题转化为:如何在可能的线路中选择n-1条,能把所有城市(顶点)连起来,且总耗费(各边权值之和)最小。
定义:
生成树中边的权值(代价)之和最小的树。
构造最小生成树的准则:
- 必须只使用该网中的边来构造最小生成树;
- 必须使用且仅使用n-1条边来联结网络中的n个顶点;
- 不能使用产生回路的边。
实例:
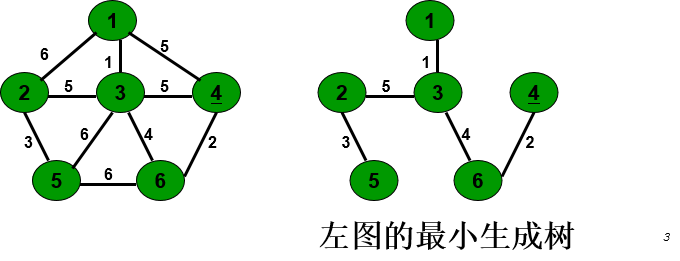
普里姆(Prim)算法
普里姆方法的思想:
1)在图中任取一个顶点K作为开始点,令U={k},W=V-U,其中V为图中所有顶点集,
2)然后找一个顶点在U中,另一个顶点在W中的边中最短的一条,找到后,将该边作为最小生成树的树边保存起来,并将该边顶点全部加入U集合中,并从W中删去这些顶点,然后重新调整U中顶点到W中顶点的距离, 使之保持最小,
再重复此过程,直到W为空集止。求解过程参见下页图。
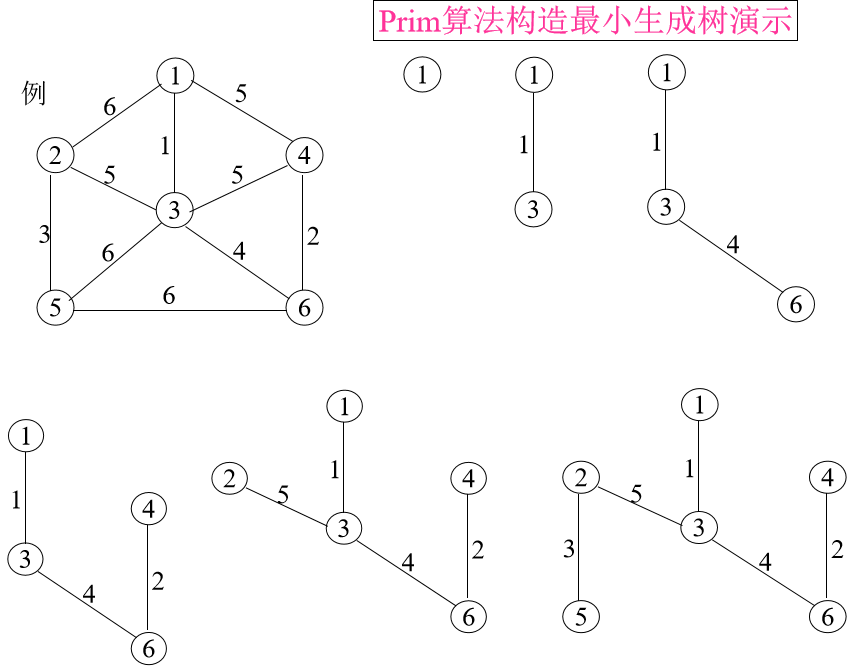
简单地说,此过程是不断地在W中找出与U里边相连的权值最小的边。
算法的基本思想
设置一个辅助数组T,对当前V-U集中的每个顶点,记录和顶点集U中顶点相连接的代价最小的边:
struct { int adjvex; // U集中的顶点序号 int lowcost; // 边的权值 } T[MAX_VERTEX_NUM];
U为生成树上的顶点集,V-U为剩余顶点集,T[j]用于存储连接V-U中顶点j与U中顶点的权值最小的边及权值。
每次从数组T中取出权值最小的边加入到树中(用权值为0为来代表顶点已加入生成树集U)。
1,初始化辅助数组,出发点加入U
2,对其余顶点
2.1 求出下一个加入树的顶点K。
2.2 输出加入树的边,将顶点K并入U
2.3 修改其它顶点的最小边。
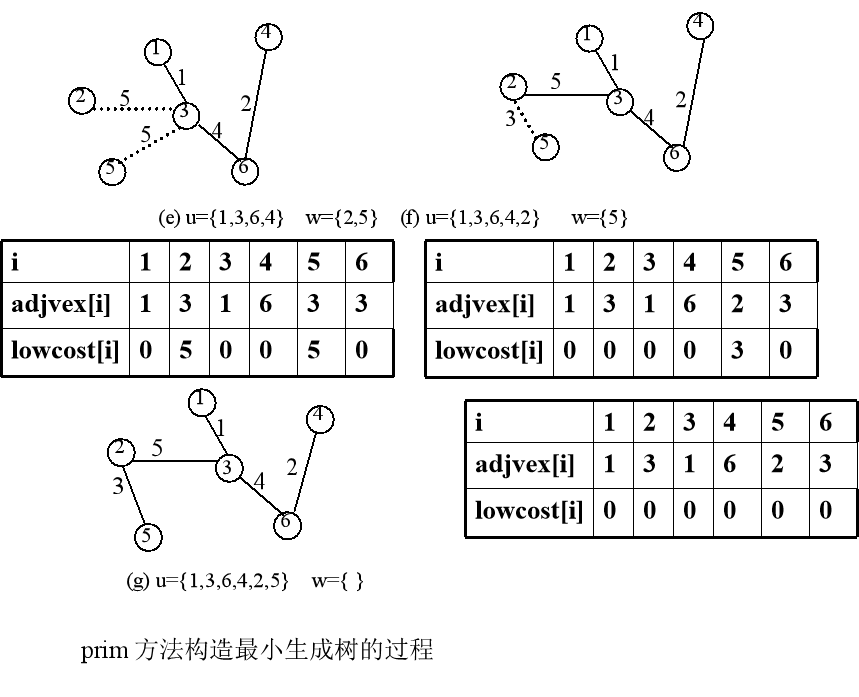
假设开始顶点就选为顶点1,故首先有U={1},W={2,3,4,5,6}
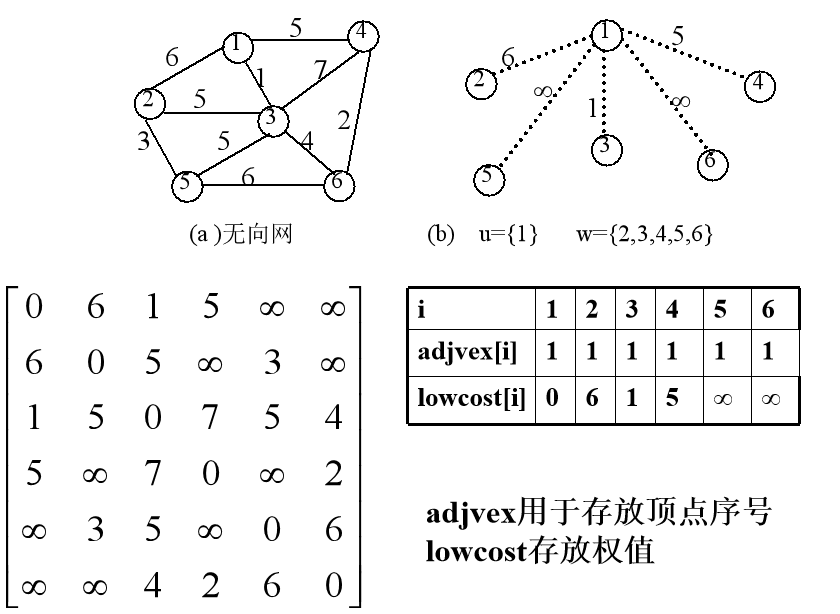
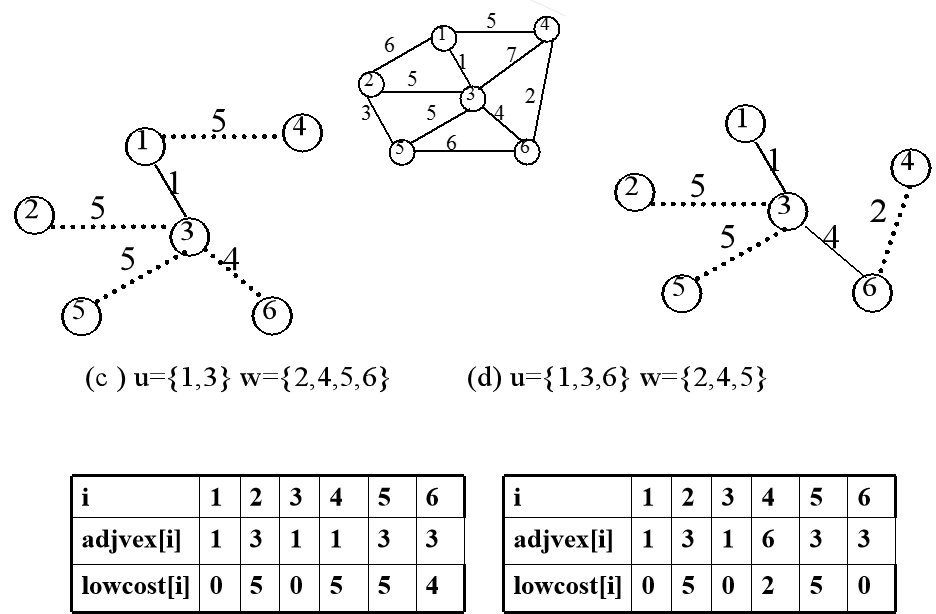
解释:第一个顶点1,它连接到3的权值最小为1,所以加入生成树中,并令T中1与3相连的边权值为0,同时加入与顶点3相连边的权值。不断重复此操作,直到w完毕。
算法实现:
void MiniSPanTree_PRIM(MGraph G, VertexType u) { int k, j, i, minCost; k = LocateVex(&G, u); //返回u在图G中的位置 for(j=0; j<G.vexnum; ++j) // 初始化辅助数组 { if(j != k){ T[j].adjvex = k; T[j].lowcost = G.A[k][j]; } } T[k].lowcost = 0; for(i=1; i<G.vexnum; ++i) /*G.vexnum-1次循环,寻找当前最小权值的边*/ { minCost = MAXINF; for(j=0; j<G.vexnum; ++j) /*求生成树的下一个顶点*/ { if(T[j].lowcost < minCost && T[j].lowcost != 0){ minCost = T[j].lowcost; k=j; } } printf("(%c, %c), %d ", G.v[T[k].adjvex], G.v[k], T[k].lowcost); /*输出生成树的边*/ T[k].lowcost = 0; /*标记顶点k已加入生成树*/ for(j=0;j<G.vexnum; ++j) /*顶点k加入生成树后重新选择最小边*/ { if(T[j].lowcost != 0 && G.A[k][j] <T[j].lowcost){ T[j].adjvex = k; T[j].lowcost = G.A[k][j]; } } } }
时间复杂度:
在普里姆算法中,第一个进行初始化的for循环语句的执行次数为n-1,第二个for循环中又包括了两个for循环,执行次数为2(n-1)2 ,所以时间复杂度为O(n2)
克鲁斯卡尔(kruskal)算法
1. 克鲁斯卡尔算法基本思想
克鲁斯卡尔算法的基本思想是:
将图中所有边按权值递增顺序排列,依次选定取权值较小的边,但要求后面选取的边不能与前面选取的边构成回路,
若构成回路,则放弃该条边,再去选后面权值较大的边,n个顶点的图中,选够n-1条边即可。
例如,对上图中无向网,用克鲁斯卡尔算法求最小生成树的过程见下图。
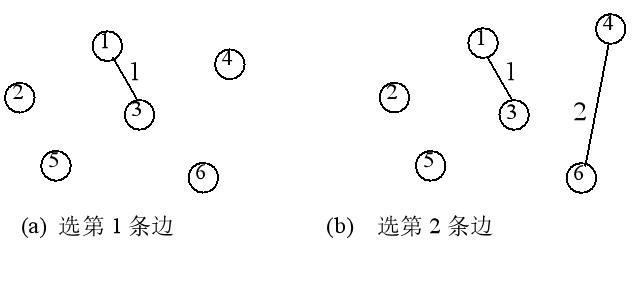
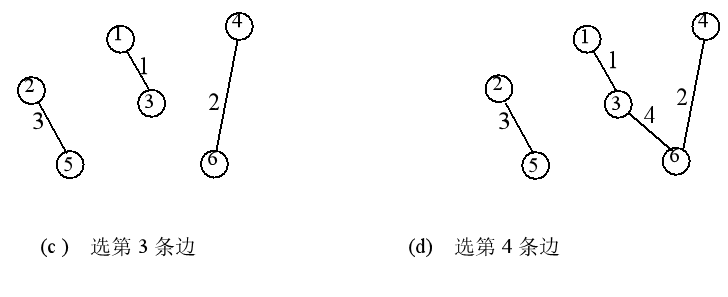

这一过程相当于选点加入树中。
kruskal算法的关键:如何判断加入的边是否形成回路。可以采用将各顶点划分为不同集合的方法来解决,每个集合中的顶点表示一个无回路的连通分量。
因此,设计一个数组int vset[MAXV],利用vset[i]来判定各顶点是否属于同一集合中。其初始值为vset[i]=i(i=0,1,...,MAXV-1),i为顶点所在集合的编号,表示各顶点在不同的集合上。
算法实现:
#define MAXE //最大边数 # define MAXV //最大顶点数 typedef struct { int v1; int v2; /*v1、v2是两 个顶点的序号*/ int weight; //边权 }Edge; // 边集类型数据结构 void kruskal(Edge GE[], int n, int e) { int i, j, m1, m2, s1, s2, k; int vset[MAXV]; for(i=0; i<n;i++) /* 初始化辅助数组 */ { Vset[i] = i; } k = 0; /*生成树中边的数目,初值为0*/ j = 0; /*边集数组GE的下标,初值为0*/ while(k<=n-1) /*生成树中的边数小于n条时继续循环*/ { m1 = GE[j].v1; m2 = GE[j].v2; /*从边集数组GE中取出一条边的两个顶点*/ s1 = vset[m1]; s2 = vset[m2]; /*分别得到两个顶点所在集合的编号*/ if(s1 != s2) /*两个顶点属于不同的集合,将该边加入最小生成树*/ { printf("(%d, %d), %d", m1, m2, GE[j].weight); k++; /*生成树的边数加1*/ vset[m2] = s1; /*使得两个集合编号相同*/ } j++; /*扫描下一条边*/ } }
假设,n为图中顶点个数,e为图中边的个数。在kruskal中,while循环是影响时间效率的主要操作,其循环次数最多为e次,所以克鲁斯卡尔算法的时间复杂度为O(e)。