[SHOI2012]随机树

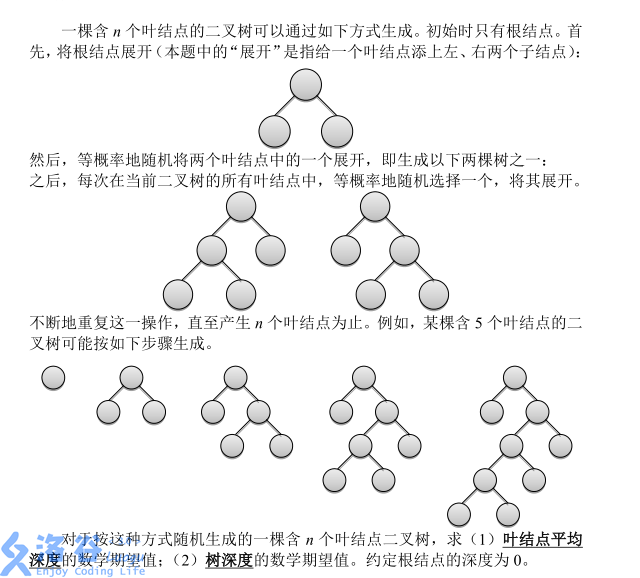
Description：

Hint：

Solution:

(第一问比较水)

(设f[i]为i片叶子的二叉树的平均期望深度)

有 (f[i]=frac{f[i-1]*(i-1)+f[i-1]+2} {i})

(f[i]=f[i-1]+ frac{2}{i}​)

第二问就非常神仙了

设 (f[i][j]) 为(i)片叶子且树的深度大于(j​)的概率

考虑枚举左右子树

(f[i][j]=sum_{k=1}^{i-1} f[k][j]+f[i-k][j]-f[k][j]*f[i-k][j])

(Ans=sum_{i=1}^{n-1}f[n][i])

证明详见： https://www.luogu.org/paste/zuloat8v

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
int opt,n;
double ans;
double g[105],f[105][105];

int main()
{
    scanf("%d%d",&opt,&n);
    if (opt==1)
    {
        g[1]=0;
        for (int i=2;i<=n;i++) g[i]=g[i-1]+2.0/i;
        printf("%.6lf",g[n]);
    }
    else
    {
        for (int i=1;i<=n;i++) f[i][0]=1;
        for (int i=2;i<=n;i++)
            for (int j=1;j<i;j++)
            {
                for (int k=1;k<i;k++)
                    f[i][j]+=f[k][j-1]+f[i-k][j-1]-f[k][j-1]*f[i-k][j-1];
                f[i][j]/=(i-1);
            }
        for (int i=1;i<n;i++) ans+=f[n][i];
        printf("%.6lf",ans);
    }
}