再论EM算法的收敛性和K-Means的收敛性

标签（空格分隔）： 机器学习

---

（最近被一波波的笔试+面试淹没了，但是在有两次面试时被问到了同一个问题：K-Means算法的收敛性。在网上查阅了很多资料，并没有看到很清晰的解释，所以希望可以从K-Means与EM算法的关系，以及EM算法本身的收敛性证明中找到蛛丝马迹，下次不要再掉坑啊。。）

EM算法的收敛性

1.通过极大似然估计建立目标函数：

(l( heta) = sum_{i=1}^{m}log p(x; heta) = sum_{i=1}^{m}logsum_{z}p(x,z; heta))

通过EM算法来找到似然函数的极大值，思路如下：
希望找到最好的参数( heta)，能够使最大似然目标函数取最大值。但是直接计算 (l( heta) = sum_{i=1}^{m}logsum_{z}p(x,z; heta))比较困难，所以我们希望能够找到一个不带隐变量(z)的函数(gamma(x| heta) leq l(x,z; heta))恒成立，并用(gamma(x| heta))逼近目标函数。
如下图所示：

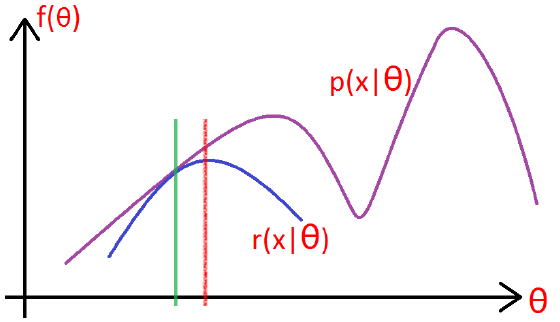
• 在绿色线位置，找到一个(gamma)函数，能够使得该函数最接近目标函数，
• 固定(gamma)函数，找到最大值，然后更新( heta),得到红线；
• 对于红线位置的参数( heta)：
• 固定( heta)，找到一个最好的函数(gamma)，使得该函数更接近目标函数。
  重复该过程，直到收敛到局部最大值。

2. 从Jensen不等式的角度来推导

令(Q_{i})是(z)的一个分布，(Q_{i} geq 0)，则：

$l( heta) = sum_{i=1}^{m}logsum_{z^{(i)}}p(x^{(i)},z^{(i)}; heta) ( ) = sum_{i=1}^{m}logsum_{z^{(i)}}Q_{i}(z^{(i)})frac{p(x^{(i)},z^{(i)}; heta)}{Q_{i}(z^{(i)})}( )geq sum_{i=1}^{m}sum_{z^{(i)}}Q_{i}(z^{(i)})logfrac{p(x^{(i)},z^{(i)}; heta)}{Q_{i}(z^{(i)})}$

(对于log函数的Jensen不等式)

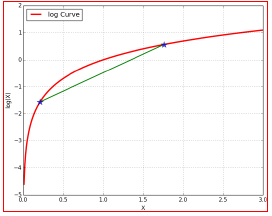
3.使等号成立的Q

尽量使(geq)取等号，相当于找到一个最逼近的下界：也就是Jensen不等式中，(frac{f(x_{1})+f(x_{2})}{2} geq f(frac{x_{1}+x_{2}}{2}))，当且仅当(x_{1} = x_{2})时等号成立(很关键)。

对于EM的目标来说：应该使得(log)函数的自变量恒为常数，即：
(frac{p(x^{(i)},z^{(i)}; heta)}{Q_{i}(z^{(i)})} = C)
也就是分子的联合概率与分母的z的分布应该成正比，而由于(Q)是z的一个分布，所以应该保证(sum_{z}Q_{i}(z^{(i)}) = 1)
故(Q = frac{p}{p对z的归一化因子})

(Q_{i}(z^{(i)}) = frac{p(x^{(i)},z^{(i)}; heta)}{sum_{z}p(x^{(i)},z^{(i)}; heta)})
(= frac{p(x^{(i)},z^{(i)}; heta)}{p(x^{(i)}; heta)} = p(z^{(i)}|x^{(i)}; heta))

4.EM算法的框架

由上面的推导，可以得出EM的框架：

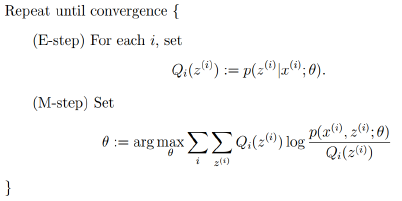
回到最初的思路，寻找一个最好的(gamma)函数来逼近目标函数，然后找(gamma)函数的最大值来更新参数( heta):

• E-step: 根据当前的参数( heta)找到一个最优的函数(gamma)能够在当前位置最好的逼近目标函数；
• M-step: 对于当前找到的(gamma)函数，求函数取最大值时的参数( heta)的值。

K-Means的收敛性

通过上面的分析，我们可以知道，在EM框架下，求得的参数( heta)一定是收敛的，能够找到似然函数的最大值。那么K-Means是如何来保证收敛的呢？

目标函数

假设使用平方误差作为目标函数：
(J(mu_{1},mu_{2},...,mu_{k}) = frac{1}{2}sum_{j=1}^{K}sum_{i=1}^{N}(x_{i}-mu_{j})^{2})

E-Step

固定参数(mu_{k}), 将每个数据点分配到距离它本身最近的一个簇类中：

[ gamma_{nk} = egin{cases} 1, & ext{if $k = argmin_{j}||x_{n}-mu_{j}||^{2}$ } \ 0, & ext{otherwise} end{cases} ]

M-Step

固定数据点的分配，更新参数（中心点）(mu_{k}):
(mu_{k} = frac{sum_{n}gamma_{nk}x_{n}}{sum_{n}gamma_{nk}})

所以，答案有了吧。为啥K-means会收敛呢？目标是使损失函数最小，在E-step时，找到一个最逼近目标的函数(gamma)；在M-step时，固定函数(gamma)，更新均值(mu)（找到当前函数下的最好的值）。所以一定会收敛了~