求二维数组最大子数组和 刘博&徐梦迪

这次的课堂练习是在上次求数组最大子数组和的基础上的延伸--求二维数组最大子数组和

我们的解题思路大致是这样的. 最简单的思路是想到的就是通过四层循环实现最大子数组和的查找，但这样的复杂度是比较大的。

起先我们只知道利用枚举法求二维数组的值，忽略了时间复杂度的要求。怎样能够快捷的找到二维的最大子数组呢？动态规划是一个简便的算法。

补充知识：

动态规划是为了使获取的决策序列在某种条件下达到最优。是一种将多阶段决策过程转化为一系列单个问题，然后逐个求解的程序设计方法。

于是我们两个采用了动态规划，这个想法的的思路是利用三层循环，就可以大大减小时间复杂度。

 a) 首先求出p[i][j]，表示以（0,0）为起点，以(i,j)为终点的的连续子数组的和；

部分代码如下：

int getMaxSub(int **a,int n,int m){
 if(m==0||n==0)//对于边界
  return 0; int **p=new int*[n];
 int i,j;
 for(i=0;i<n;i++){
  p[i]=new int[m];
  for(j=0;j<m;j++){
   if(i==0){
    if(j==0)
     p[i][j]=a[i][j];
    else
     p[i][j]=p[i][j-1]+a[i][j];
   }
   else{
    if(j==0)
     p[i][j]=p[i-1][j]+a[i][j];
    else
     p[i][j]=p[i][j-1]+p[i-1][j]-p[i-1][j-1]+a[i][j];
   }
  }
 }

 b、计算B(a,c,i) 从第a行到第c行并且第i列竖条元素的和。计算二维数组最大子数组的和，时间复杂度为O(N*M*M)

 B(a,c,i)=p[c][i]-p[c][i-1]-p[a-1][i]+p[a-1][i-1]，即起点是第a行，终点是第c行，然后转换为一维连续子数组的和。

该部分代码如下：

int temp;
int max;
int ans=-0xfffff;
 
    if(m==1){
  for(i=0;i<n;i++){
   for(j=i;j<n;j++){
    if(i==0){
     temp=p[j][m-1];
    }else{
     temp=p[j][m-1]-p[i-1][m-1];
    }
    if(ans<temp)
     ans=temp;
   }
  }
 }else{
  for(i=0;i<n;i++){
   for(j=i;j<n;j++){
   if(i==0){
     temp=p[j][m-1]-p[j][m-2];
    }else{
     temp=p[j][m-1]-p[j][m-2]-p[i-1][m-1]+p[i-1][m-2];
    }
  for(int k=m-2;k>=0;k--){
     if(temp<0)
      temp=0;
     if(i==0){
      if(k==0)
       temp+=p[j][k];
      else
       temp+=p[j][k]-p[j][k-1];
     }else
     {
      if(k==0)
       temp+=p[j][k]-p[i-1][k];
      else
       temp+=p[j][k]-p[j][k-1]-p[i-1][k]+p[i-1][k-1];
     }
     
     if(ans<temp)
      ans=temp;
    }
    
   }
  }
 }
 
 return ans;
}

c.主函数

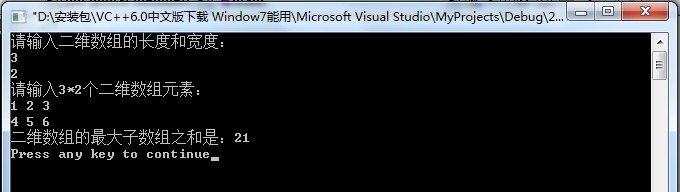
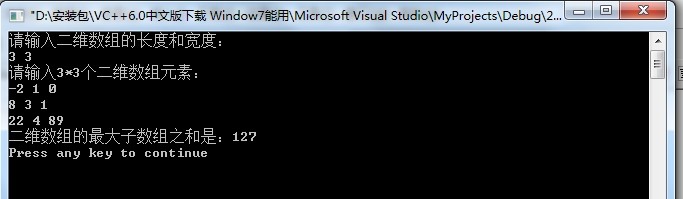
int main(void){
 int n,m;
 printf("请输入二维数组的长度和宽度：
");
 scanf("%d %d",&n,&m);
 int i,j;
 int **a=new int*[n];
 printf("请输入%d*%d个二维数组元素：
",n,m);
 for(i=0;i<n;i++){
  a[i]=new int[m];
  for(j=0;j<m;j++){
   scanf("%d",&a[i][j]);
  }
 }
 int ans=getMaxSub(a,n,m);
 printf("二维数组的最大子数组之和是：%d
",ans);
 return 0;
}

结果展示：