变步长梯度下降法

关于最优化算法的框架见
最优化算法确定迭代步长【线搜索技术】

迭代公式(x_{k+1}=x_k+alpha_kd_k)
其中(alpha_k)为第k次迭代步长，(d_k)为第k次迭代方向；

变步长梯度下降法就是每次迭代，步长都需要计算
定步长梯度下降发每次步长都为定值；算法见
最优化算法【最小二乘法和梯度下降法（固定步长）】

关于步长的确定，本算法采用非精确线搜索的Armijo准则

示例函数

[f(x_1,x_2)=100(x_1^2-x_2^2)^2+(x_1-1)^2 ]

求极小值

matlab代码

function [x,val,LOOS_t] = c_gradientDescent(func,gfunc,x0,iterate)
%c_gradientDescent - 变步长梯度下降法
%
% Syntax: [R,LOOS_t] = c_gradientDescent(func,gfunc,x0)
%
% R为所求极值点和极值矩阵，LOOS_t为迭代过程，函数值变�?

    maxk=iterate;
    LOOS_t=zeros(1,maxk);
    rho=0.5;Sigma=0.3;
    k=0;epsilon=1e-5;

    while k<maxk
        g=gfunc(x0);
        d=-g;

        if norm(d)<epsilon
            break;
        end
        m=0;mk=0;
        while m<20
            if func(x0+rho^m*d)<func(x0)+Sigma*rho^m*g'*d
                mk=m;
                break;
            end
            m=m+1;
        end     
        x0=x0+rho^mk*d;
        k=k+1;
        LOOS_t(1,k)=func(x0);
%         disp(x0);
    end
    x=x0;
    val=func(x0);
end

main函数代码

clc;
close all;
iterate=20;
func=@(x) 100*(x(1)^2-x(2))^2+(x(1)-1)^2;
gfunc=@(x) [400*x(1)*(x(1)^2-x(2))+2*(x(1)-1),-200*(x(1)^2-x(2))]';
x0=[-1.2,1]';
[x,val,LOOS_t] = c_gradientDescent(func,gfunc,x0,iterate);
disp(x);
disp(val);
figure(1);
plot(1:iterate,LOOS_t);

u=linspace(0,2,100);
v=linspace(0,2,100);
[uu,vv]=meshgrid(u,v);
ww=100*(uu.^2-vv).^2+(uu-1).^2;
figure(2);
mesh(uu,vv,ww);
set(get(gca, 'XLabel'), 'String', 'x1');
set(get(gca, 'YLabel'), 'String', 'x2');
set(get(gca, 'ZLabel'), 'String', 'f(x1,x2)');
[xx,min_f]=fmincon(func,x0,[],[],[],[],[0;0],[2;2]);
hold on;
plot3(xx(1),xx(2),min_f,'rp','MarkerSize',20);
text(xx(1),xx(2),min_f,['(',num2str(xx(1)),',',num2str(xx(2)),',',num2str(min_f),')'],'color','r');

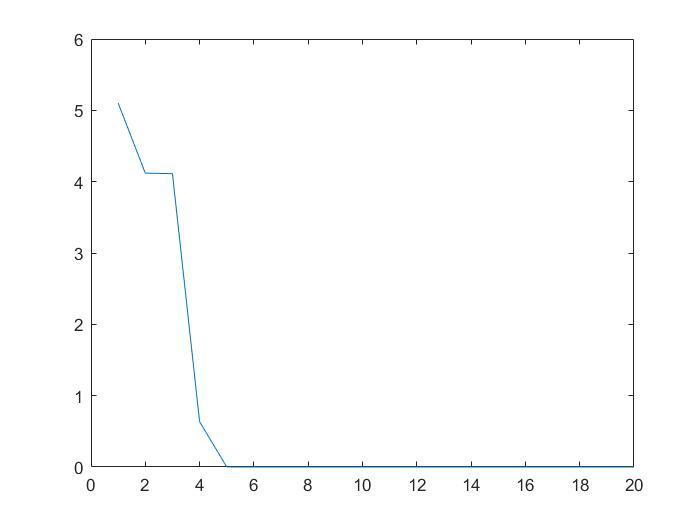
效果

函数值随迭代变化

matlabfmincon函数计算结果及函数图像

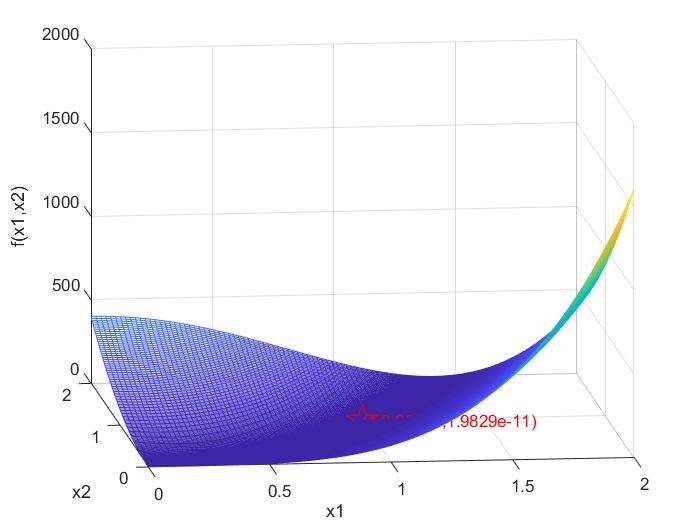
conclusion

1. 此算法计算结果和matlab函数计算结果相同，精度较高；
2. 和其他算法比较，收敛速度较慢。