- ElGamal体制
(1)参数设置
① 随机选择大素数p,且要求p-1有大素因子,g是Zp*
的生成元。
② 随机选取一个整数x(1<x<p-1),计算y=g^xmodp
公开密钥(公钥):k1=(y,g,p)
私有密钥(私钥):k2=x
(2)加密
消息明文为m,随机选取整数r,1<r<p-1,计算:
c=grmodp,c'=myrmodp
将密文(c,c')发送给接收方。
(3)解密

- 注1:发送方A利用接收方B的公钥进行加密,接收方利用自己的私钥进行解密。
- 注2:r解密过程中用不到,所以不需告知接收者。另,每次加密r的选取都不同,好处:
①如果每次r值不变均相同,则有:
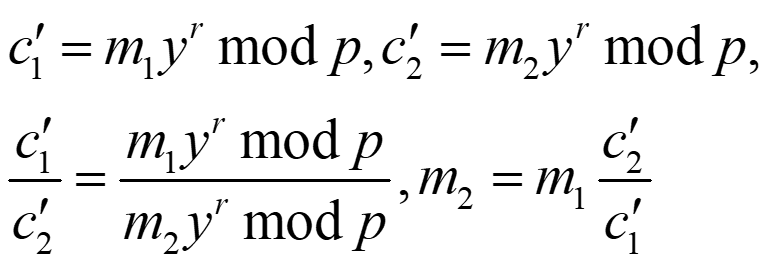
②相同明文的密文不同,不同明文的密文可能相同,增加破译难度。
例 发送方为A,接收方为B,B选择素数p=13171,生成元g=2,私钥 x=23,A将消息m=bu加密后发送给B,消息明文按英文字母表m=bu=0120
解:密钥生成:
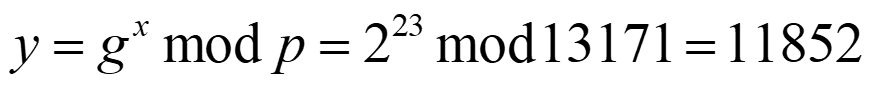
公钥:y=11852,g=2,p=13171
私钥:x=23
加密:
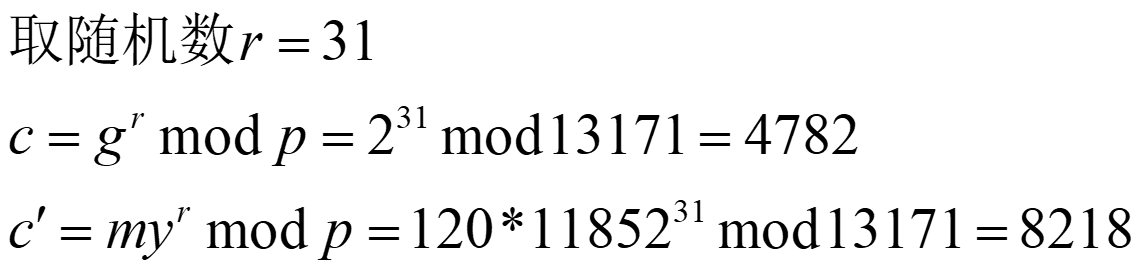
解密:
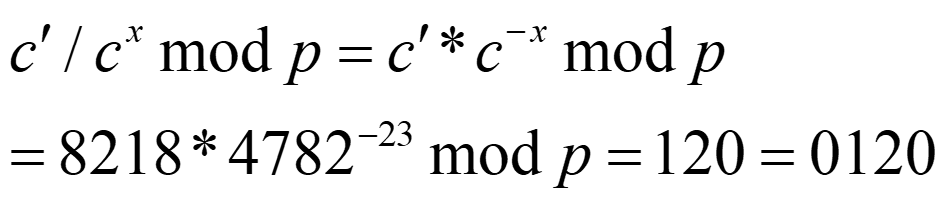
(4)攻击
攻击者需由y,g,p及y=g^xmodp求出x,该问题称为离散对数问题:
x=loggy
注:该问题目前还没有被解决,是公认的数学难题之一。
注:有如下一些攻击方法:小步大步算法、指数积分法,但威胁不大。
量子计算机若出现,则可以很轻松穷举破译离散对数问题。