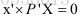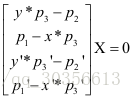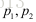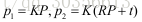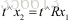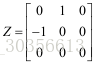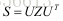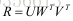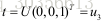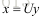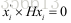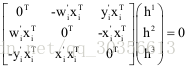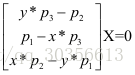其中主要涉及到的算法分别是:8点-DLT方法计算基础矩阵,8点-DLT方法计算单应矩阵,根据基础矩阵分解得到相机位姿和3D匹配点,根据单应矩阵分解得到相机位姿和3D匹配点。
一、8点DLT方法计算基础矩阵:
(参考高翔slam14讲)
首先应明白基础矩阵的几何意义是什么?它解决的问题是如何通过两幅图像中的像素匹配点来估算两幅图像点的变换矩阵F(基础矩阵)。
设的空间位置为: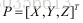
则有: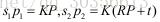
取齐次坐标有:
取
两边同时左乘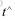
两边同时左乘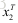
将p1,p2带入上式得到:
从而得到对极约束的代数表示,其中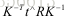
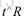
然后根据8点法求解本质矩阵E,进而求解基础矩阵F
设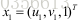
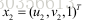
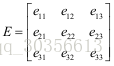

用SVD方法求解上述方程,E的解对应的是最小奇异值对应的奇异向量,证明过程参考《Multiple view geometry in computer vision》.page592 A5.3

由此求得本质矩阵E,进而求取基础矩阵F
二、本质矩阵分解得到旋转矩阵R和平移向量t
(参考 multiple view geometry in computer vision 9.6节的相关知识)
上个算法中通过8点法得到了本质矩阵E,但实际上本质矩阵需要满足自身的约束,对于一个本质矩阵E来讲,它的奇异值有两个相等,并且第三个为零。证明如下:
上面可以看出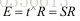
则
如果一个实反对称矩阵S,则可以将S分解为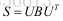
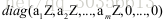
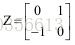
因此,S可以分解为: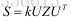
引入正交矩阵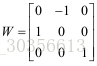

不计尺度得到:
由于W,U,R都是正交矩阵,因此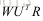
从而得到
其中根据(1)可得
R是一个旋转矩阵可以被写成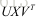
其中
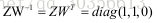
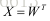
由此可得到: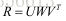
由于

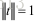
同时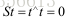
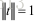
证明参考multiple view geometry in computer vision A5.3 P592 如下:
由于U是酉矩阵,根据范数的酉不变性因此存在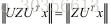




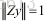
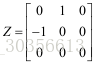
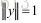
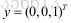
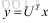
因此得到x的解为U的最后一行,即U的最小向量。证闭。
上述可以得到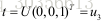
综上可得,E可以被分解为四种结果,分别为:
将其用几何的形式表示得到:
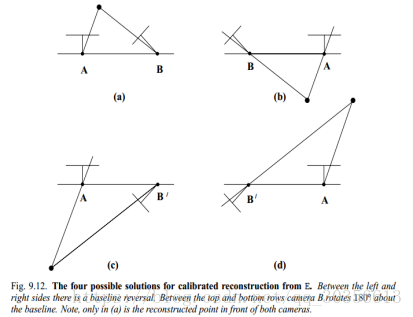
其中bcd图有负的深度值,因此可以舍去,只要a图符合要求。
所以根据在两个相机坐标系下坐标点的深度可以筛选出正确的结果,从而得到唯一正确R和t
三、8点DLT方法计算单应矩阵H:
(参考multiple view geometry in computer vision 第四章 P89)
单应性矩阵与基础矩阵的不同在于,单应性矩阵是针对平面上点集合来讲的,而基础矩阵基于三维点集合来讲
对于二维到二维的点集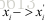
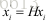
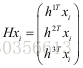
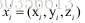
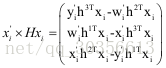
由于上式矩阵质为2,因此只有两个不相关的向量,因此针对每一对匹配点,都有:
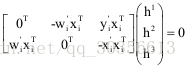
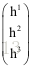
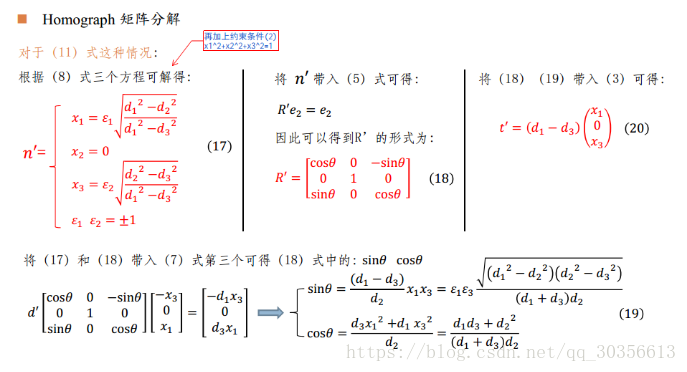
四、单应矩阵分解得到旋转矩阵R和平移向量t
(参考文章:Motion and Structure from Motion in a Piecewise Planar Environment)
(同时参考吴博注释版的ORBSLAM的PPT)



从而得到R和t的8种组合,然后根据匹配点在相机坐标系下的深度值以及重投影误差来得到一组最优值,从而结算出当前相机位姿。
五、三角测量得到匹配三维点坐标
通过基础矩阵和单应性矩阵求解相机位姿过程中并没有利用到匹配点的三维点坐标,但在SLAM中的建图下计算匹配点的三维坐标是必要的,因此,我们用三角测量的方式来得到三维点坐标,如上所示,已经得到了相机的位姿R,t,而且相机的内参数矩阵是已知的,结合两者,我们可以得到由相机像素坐标到三维点坐标点的变换矩阵P=T*K,其中T是由R和t决定的相机位姿变换矩阵,K为相机的内参数矩阵。
因此对于每一匹配点我们都有x=P*X,x’=P’*X,x,x’分别为匹配点在帧1和帧2的像素坐标,P,P’分别为相机变换矩阵,由于存在尺度问题,因此,我们用齐次坐标进行求解,对于齐次坐标存在x叉乘P*X,即:
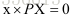
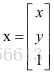
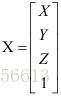
令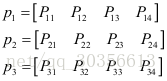
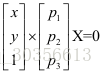
同理可以得到