约瑟夫环问题是一个经典的数学问题,背景故事参考百度百科,其原始问题如下:
0,1,,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
比较直接的想法是通过链表模拟游戏,直到最后只剩一个元素,但这样的时间复杂度是O(nm),显然不行。类似问题通过数学方法找到规律会简单的多,其实很多递归以及动态规划题目也是通过数学方法找递推式即可简单解出。
记上述问题的解为f(n,m)。则第一个被删除的数为(m-1)%n。此时,转化为由m%n开始的,规模为(n-1,m)的相同问题结构约瑟夫环问题。所以此问题可以通过递归来求解,但要知道每次迭代之后,新元素和就元素的一一对应关系。以第一次迭代为例:
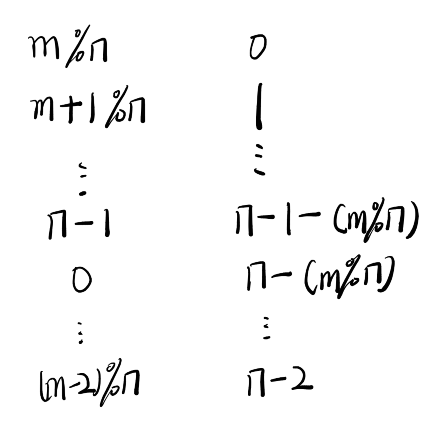
把新元素编号记为x,旧元素编号记为y,那么新旧编号的对应公式为
y = (x + m) % n
由此可得
f(n,m) = (f(n-1,m) + m) % n n>1
f(1,m) = 0
public int lastRemaining(int n, int m) { int f = 0; for (int i = 2; i <= n; i++) { f = (f + m) % i; } return f; }
其中f是f(1,m)的解。