网络流

首先我们先明确一下网络流是什么，你可以想象一堆水管，有一个可以无限放水的水厂，和接受水的房间。

水厂和这个房间之间由许多水管连起来，可是每个水管都会有一个宽度。当然如果流过去的水要大于这个宽度，那这个点当然就不能走，那水厂就只能减少水的供应，这样大体就是网络流了。

我们再抽象一点：

所谓网络或容量网络指的是一个连通的赋权有向图 D= （V、E、C） ， 其中V 是该图的顶点集，E是有向边(即弧)集，C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流，这是定义在网络上的非负函数，它一方面受到容量的限制，另一方面除去起点和终点以外，在所有中途点要求保持流入量和流出量是平衡的。

概念：

• 源点：只有流出去的点
• 汇点：只有流进来的点
• 流量：一条边上流过的流量
• 容量：一条边上可供流过的最大流量
• 增广路径：从源点到汇点，符合网络流性质的一条路径
• 残量：一条边上的容量-当前流量（也可以理解成动态的容量）
• 残余网络：即为一条管道被占用了一部分流量之后所剩下的流量形成的图
• 割和最小割：给定一个网络 G = (V, E)G=(V,E) ，源点为 S，汇点为 T。若一个边集 E′⊆ E 被删去之后，源点 S和汇点 T不再连通，则称该边集为网络的割。边的容量之和最小的割称为网络的最小割。

性质：

1. 首先是最重要的一点，每条边流量都<=容量，也是最好理解的。（容量限制性）
2. 其次我们都知道地球上的水资源是平衡的，因为有流入就有流出，在网络流中也差不多是这样，除了源点和汇点以外，所有点的流入流量==流出流量。（反对称性）
3. 每条边的流量 == 该条边的反向边的流量的相反数（因为流过去的量就相当于从它的反向边流过来相反的量）。这个性质很有用，具体到后面再讲。（流守恒性）
4. 任取一个割，其容量大于最大流的流量，记为：割>=最大流。（这个定理选学，不学也不重要）

　　　  证明：从源点到汇点的每条路径都会经过割上的最少1条边。 割掉这些边之后，把源点能到达的点放到左边，不能到达的放到右边。 显然最大流不会超过从左边到右边的边的容量之和。而这个容量之和恰恰就是割。换一种说法：我们现在要割水管，假设我现在在有水流的时候割水管，每次割水管所花费该水管的容量，当流量小于容量时，我的花费肯定比流量大。所以割>=最大流。

　     5.而当割是最小割的时候，最小割=最大流。（这个定理选学，不学也不重要）

　　　证明:首先我们知道当流是最大流时，途中肯定不存在增广路，如果存在说明这个流不是最大流。

　　 6.上文4,5定理即是最小割最大流定理。

这样我们先举一个例子，跑一遍最大流。

如图：

 

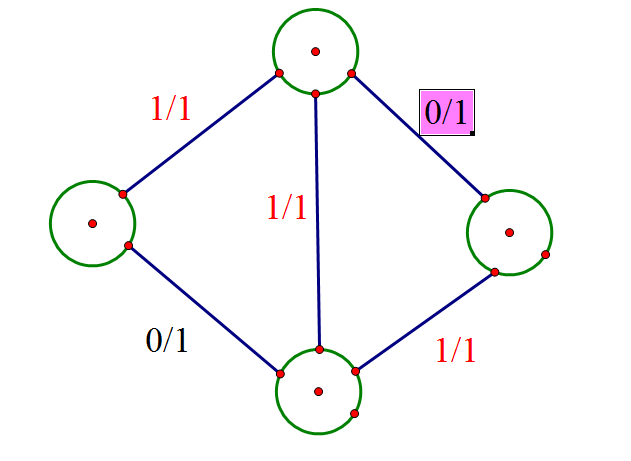
这个图很明显如果按上图这样走的话，明显是错的，所以我们上文的反向边就有了作用，就可以反悔了，之前的反思告诉我们，在一条边流过去之后，我们需要反过来建一条边。 如果边 u（只是一个名字）流过去了u些流量，那么我们需要建一条反过 来的边，比如叫做v 。 v的残量即为u当前的流量。

如图：左图中每条边的两个值分别是其流量和容量；右图即为残量网络（只画出了残量不为 0 的边），其中蓝色边是新建的反向边。

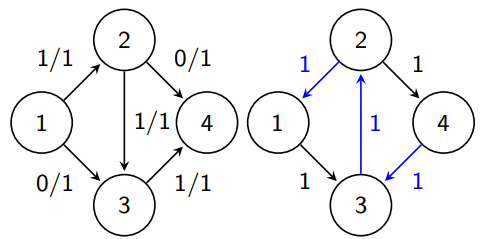
FF：

FF算法便是：当有向图中存在增广路径，即将这条增广路径加入流当中，且把对应的边建上反向边。当有向图中无法再找到增广路径的时候，此时的流即为我们所要求的最大流。(依据为最大流最小割定理)。很明显每次都会加上一定的流量，但是流量并不是可以达到无限大的，所以这个算法不会死循环，（即）但是有这样一组极端数据：

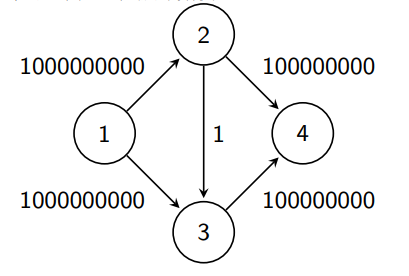
这样我们如果走2——3这条边那就会左右横跳。非常麻烦。

观察这个图，所以我们可以想到只增广最短路径。

因此EK和dinic等等许多算法应运而生：

EK(在最大流中不常用，但是费用流中常用):

其实很简单，直接从s到t广搜即可，从s开始不断向外广搜，通过权值大于0的边（因为后面会减边权值，所以可能存在边权为0的边），直到找到t为止，然后找到该路径上边权最小的边，记为mi，然后最大流加mi，然后把该路径上的每一条边的边权减去mi，直到找不到一条增广路（从s到t的一条路径）为止。

代码：

struct road {
    int from, edge;//分别是这个点从哪个点过来和那个点与这个点的连边
}pre[10000];
inline bool bfs()//相当于一个记录路径的spfa
{
    queue<int> q;
    memset(vis, 0, sizeof(vis));//vis判断是否在队列中.
    vis[s] = 1;
    q.push(s);
    while (!q.empty())
    {
        int cur = q.front();
        q.pop();
        for (int i = lin[cur]; i; i = e[i].next)
        {
            int to = e[i].to;
            if (!vis[to] && e[i].len)//这个点不在队列中，且这条边的残量要大于0
            {
                pre[to].from = cur;
                pre[to].edge = i;
                if (to == t)//如果到了终点，说明存在增广路径。
                    return 1;
                vis[to] = 1;
                q.push(to);
            }
        }
    }
    return 0;
}
int EK()
{
    int ans = 0;
    while (bfs()
    {
        int minn = inf;
        for (int i = t; i != s; i = pre[i].from)
            minn = min(minn, e[pre[i].edge].len);
        for (int i = t; i != s; i = pre[i].from)
        {
            e[pre[i].edge].len -= minn;
            e[pre[i].edge ^ 1].len += minn;//建反向边
        }
        ans += minn;最大流加上这个增广路径上的最小值
    }
    return ans;
}

费用流就把bfs换成spfa

dinic(最大流中常用)：

首先用BFS对整个图中的节点进行分层(按照搜索到达的前后顺序，即根据到源点的距离排序)。然后利用DFS对找到过的增广路径进行扩展并更新网络流。然后再次进行分层，增广。进过迭代后，如果BFS无法到底汇点，则说明不存在从源点到汇点的增广路径。搜索即告结束。此时我们得到的流一定为最大流。

代码：

inline bool bfs()
{
    int i, now; q.push(s);
    memset(deep, 0, sizeof(deep));
    deep[s] = 1;
    q.push(s);
    while (!q.empty())
    {
        now = q.front();
        q.pop();
        for (i = lin[now]; i; i = e[i].next)
            if (e[i].len && deep[e[i].to] == 0)//没有确定的层数
                deep[e[i].to] = deep[now] + 1, q.push(e[i].to);
    }
    if (deep[t] > 0)//如果汇点有层数
        return 1;
    else
        return 0;
}
int dfs(int x, int minn//当前增广路径上的最小边权)
{
    if (x == t)
        return minn; 
    for (int i = lin[x]; i; i = e[i].next)
        if (deep[e[i].to] == deep[x] + 1 && e[i].len)////寻找最短可增广路径
        {
            int w = dfs(e[i].to, min(minn, e[i].len)//相当于寻找一个最小值;
                if (w > 0)
                {
                    e[i].len -= w;
                    e[i ^ 1].len += w;
                    return w;
                }
        }
    return 0;
}
int dinic()
{
    int ans = 0;
    while (bfs())
        while (int d = dfs(s, inf))
            ans += d;
    return ans;
}