论文笔记《Accelerate CNNs from Three Dimensions: A Comprehensive Pruning Framework》

Accelerate CNNs from Three Dimensions: A Comprehensive Pruning Framework

• 2021.5.10
• ICML 2021
• https://arxiv.org/abs/2010.04879

Introduction

• 大部分的剪枝pruning方法，只看单一维度，但是单一维度过度的pruning会导致模型正确率的下降，为了缓解这一现象，本文采取方法从深度宽度分辨率三个维度共同进行剪枝操作。基于这样的目标，我们将其转化成为优化问题（其实这个思想和之前的文章一致，看成是多目标优化问题），我们通过多项式回归的方式将深度宽度分辨率与模型准确率联系在一起并进行优化。我们采用一些方法来减少计算量，细化多项式和利用迭代的剪枝和finetune来更快速地收集数据。我们只需要给定要prun掉多少，就可以在这三个维度上分别找到一个最优解

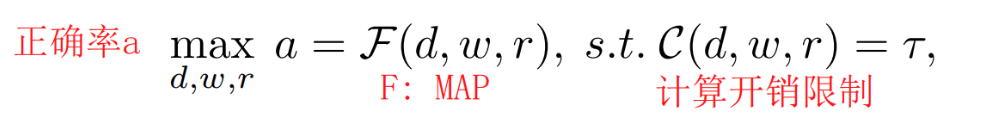
• 根据泰勒公式，任何连续函数都可以利用多项式对此进行估计。但我们需要为这个MAP(model accuracy predictor)收集大量的数据来预测参数，就可以基于拉格朗日乘数法来给出最后我们需要的((d,w,r))

• 难点在于多项式回归需大量训练数据并且会有很大的计算代价，提出了两种方法对框架进行改进

  • 1)提出了一种细化的多项式用低阶张量代替原来的张量，这个张量可以防止多项式过拟合，并确保在有限数据下也可以有准确的回归并且更简洁
  • 2)给定一个预训练模型，我们通过迭代地剪枝和微调模型来获取新模型和对应的((d,w,r))值作为MAP的数据依据

• 整体架构

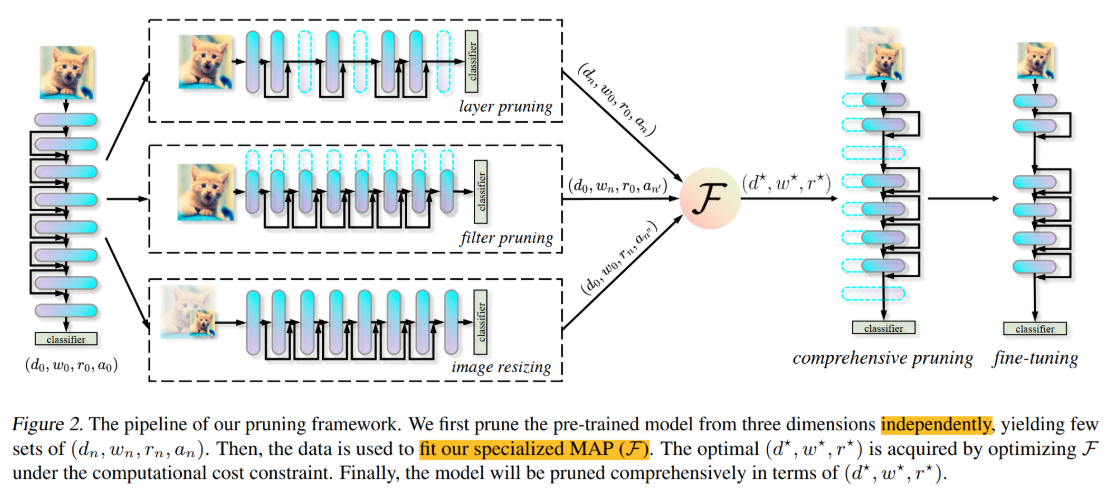
Method

SPECIALIZED MAP

• 可以将这个模型加速问题转变成如下的优化问题，给定原始模型和预期压缩比例，我们希望得到那三个参数((d,w,r))，根据之前一些工作的介绍，模型计算量和(d,w^{2},r^{2})成正比，(C(d,w,r)=dw^{2}r^{2})

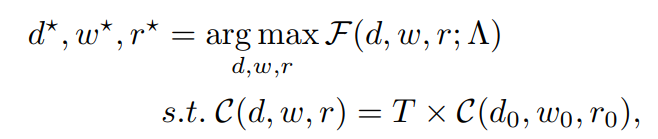
• 根据泰勒定理 任何连续函数可以用多项式估计，所以原理上我们可以训练(N)个具有不同((d,w,r))的模型，计算得到正确率(a)，利用这些数据对多项式进行回归，所以我们需要设定一个特定的(MAP)来保证即使在少量数据上也可以保证准确地回归

• 我们将这个基于多项式地MAP描述成如下，其中(Lambdainmathbb{R}^{K imes K imes K})，代表的每个参数多项式中每一项的指数，表示(K)次多项式，实际实验中设K=3

• 为了防止过拟合并且确保可以利用会有限数据回归，我们在回归过程中限制(Lambda)的阶((rank of Lambda ))，相当于是利用其Low-rank版本来进行替代，其实对于(Lambda)不过是个三阶张量，原文对此进行了如下分析，首先给出了低阶张量的定义，可以看成是多个一维向量的外积，然后将原(Lambda)中每一个值进行代替。

• 在分析中，将其转化为三个一元多项式相乘，在实验中发现取R=1足够获得很好的结果，意思就是进一步化将我们需要回归的多项式简成了三个一次多项式的乘积

Data Collection & Optimizing

• 并没有一个个的根据((d,w,r))来从开始训练模型获取数据，通过迭代剪枝和fine-tune的方法收集数据，如果某一项达到了最小值，就已经达到了全部剪枝压缩的要求，给出算法如下：T就是计算量减少的比例，rds是循环次数，实际实验中设为4，ResNet& DenseNet 在 CIFAR-10 每次finetune40个epoch。这样的数据收集方法优点在于收敛更快，中间模型作为参数

• 转换成条件约束下多个参数的优化问题，利用大一高数上的拉格朗日乘数法对此进行优化，目标函数就是(C(d,w,r)+MAP=dw^{2}r^{2}+F(...))，限制条件就是计算量缩减比例

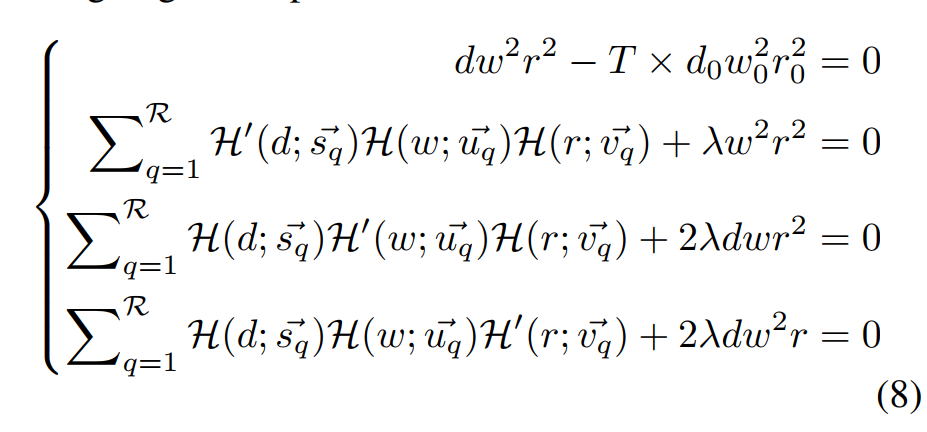
Pruning & Fine-tuning

• 通过以上算出对于某个模型的最优解((d,w,r))后，就可以对模型进行剪枝和微调，分成三个步骤：

• Pruning Layers 在模型每一层后都放置一个线性分类器，并在测试集上测准确性，每一层的分类器可以反映层的区分度，将正确率结果根据前一层进行对比，根据增益判断重要性剪掉最不重要的((Following DBP))

• Pruning Filters用BN层的比例因子作为重要性度量，BN针对batch内所有图的每一个channel，在scale和bias时对于每一个channel都存在一组参数，根据这个scale设定channel重要性((Following Slimming))

• **Fine-tuning with Smaller Images **根据减少的图片尺寸finetune，通过双线性下采样对模型进行finetune

Result

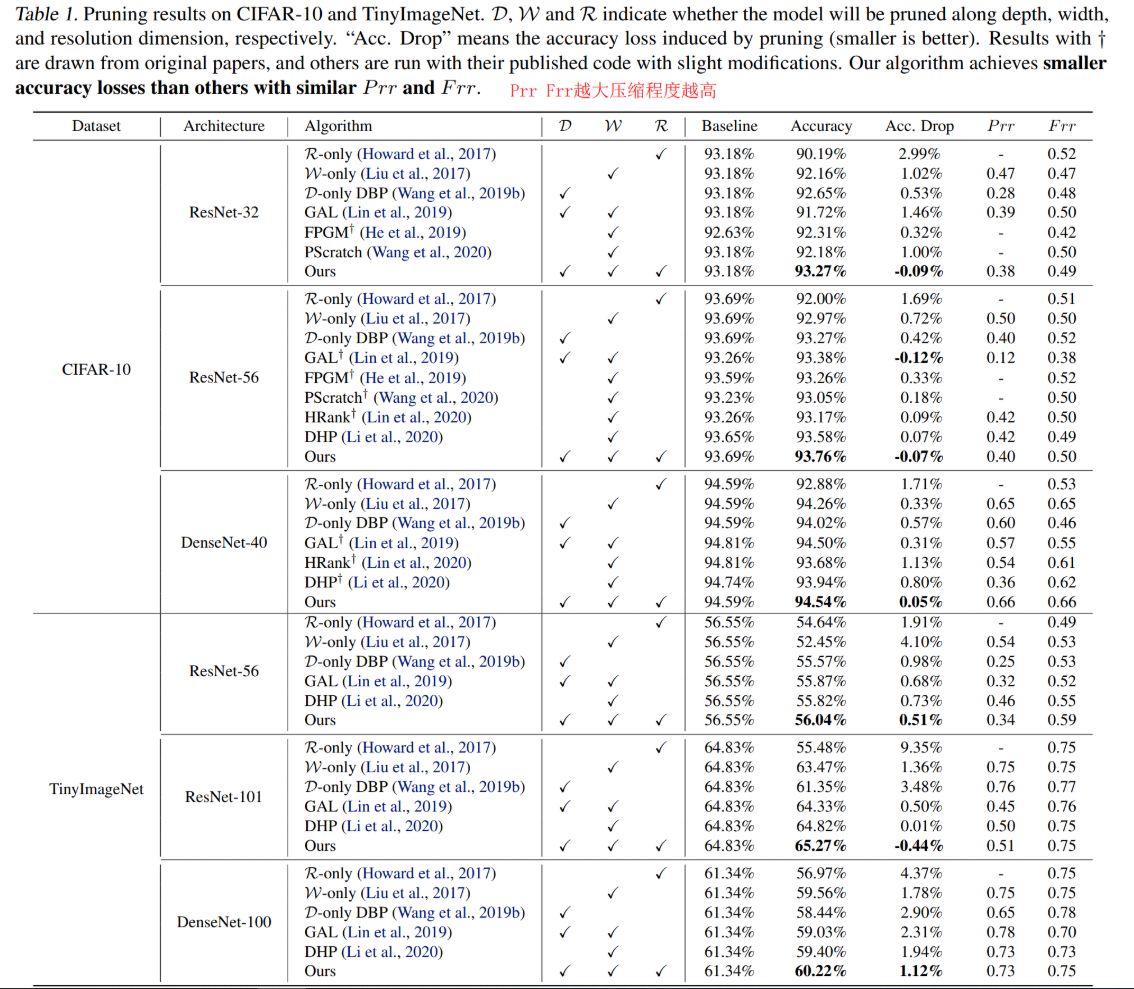
Conclusion & My Opinion

• 通过巧妙的方法收集了大量的数据，通过数学方法来拟合了所推测的模型准确率和((d,w,r))三者的关系，从三个维度进行了剪枝。与之前华为的魔方模型所采用的数学方法数据收集方法不同，这个更简单，而且和EfficientNet这种靠NAS搜出来的剪枝模型相比所需要的搜索时间少。但这个多项式公式毕竟也只是猜想，虽然有很多的AblationStudy证明了其单个参数的线性关系，但其实假设成三个一次函数的乘积后就在假设三个变量是独立的，虽然结果上是work的，但还是让人怀疑这一点，看着线性总觉得有点不靠谱，但这确实是目前在三个维度上做文章相当简单又有效的方法了，文章也很好理解。但是其对比的方法感觉都比较老了，和最新的剪枝baseline比较的结果会是我比较感兴趣的。感谢作者的工作给我带来的启发，ICML还是nb的