Java数据结构之二叉树的基本介绍与递归遍历

二叉树的基本概念：

正如我们所了解的，树是有很多中形态，但是我们规定，形如每个节点最多只能有两个子节点的一种形如称为二叉树。我们将二叉树中该节点的两个子节点分别称作为：左孩子节点和右孩子节点。该节点称为他们的双亲节点。

二叉树的结构示意图如下：

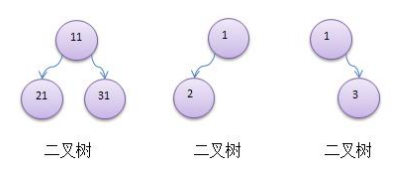
在二叉树的树状结构中，有两种特殊的二叉树值得我们关注。

首先如果该二叉树的所有叶子节点都在最后一层，并且节点的总数=2^n-1,n为层数(相当于，该二叉树最底层没有空余的位置),这样的二叉树我们称为满二叉树。

满二叉树的结构示意图如下：

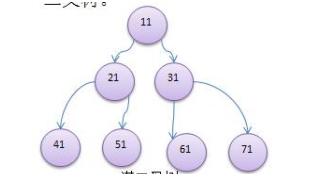
如果该二叉树的所有叶子节点都在该树的最后一层或倒数第二层，并且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，这样的二叉树我们称为完全二叉树。

完全二叉树的结构示意图如下：

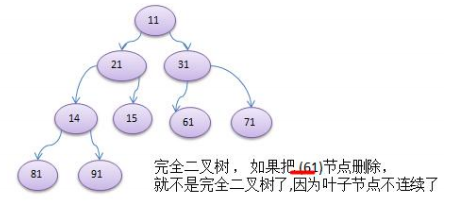
 由以上两个图我们可以了解到，满二叉树是完全二叉树的一种。

二叉树的遍历操作：

二叉树的遍历操作主要有三种：先序遍历，中序遍历，后序遍历。

(1).先序遍历：先输出父节点，再遍历左子树，再遍历右子树。

(2).中序遍历：先遍历左子树，再输出父节点，再遍历右子树。

(3).后序遍历：先遍历左子树，再遍历右子树，再输出父节点。

结论：看输出父节点的顺序，就可以确认到底是先序，中序还是后序。

下面我将用一个示意图来表示先序，中序，后序的执行过程。

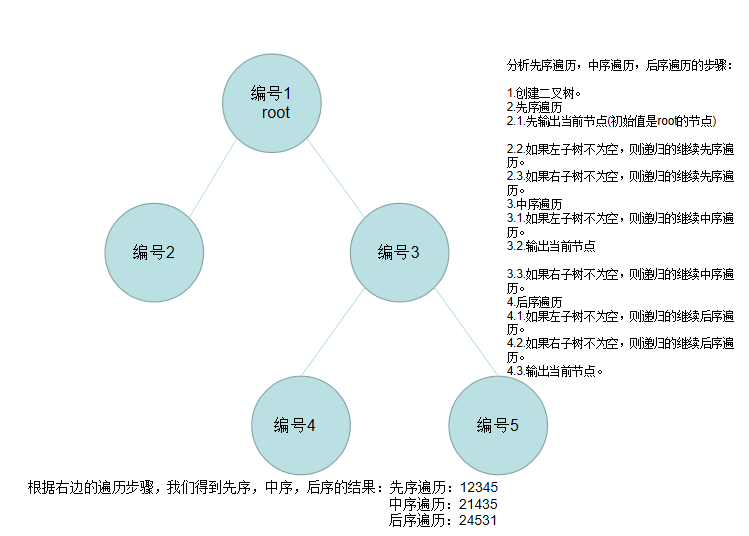
 下面我会通过代码来具体描述二叉树遍历的执行过程，具体的详解再代码的注释中说明：

package tree;

public class BinaryTreeDemo {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		//创建二叉树，这里面采用手动的创建，后面的讲解中会使用递归创建
		HeroNode root = new HeroNode(1, "java");
		HeroNode node2 = new HeroNode(2, "c");
		HeroNode node3 = new HeroNode(3, "c++");
		HeroNode node4 = new HeroNode(4, "python");
		HeroNode node5 = new HeroNode(5, "c#");
		
		BinaryTree binary = new BinaryTree();
　　　　　　　　　 //手动的创建二叉树，得到的二叉树与我们示意图中的二叉树相同
		root.setLeft(node2);
		root.setRight(node3);
		node3.setLeft(node4);
		node3.setRight(node5);
		
		//把上述创建的二叉树与我们定义的二叉树的类相关联
		binary.setRoot(root);
		binary.preOrder();
		System.out.println("=======");
		binary.infixOrder();
		System.out.println("=======");
		binary.postOrder();
		
	}

}
class BinaryTree{
	//私有化一个root节点
	private HeroNode root;

	public HeroNode getRoot() {
		return root;
	}
	//获取root节点
	public void setRoot(HeroNode root) {
		this.root = root;
	}
	//先序遍历
	public void preOrder(){
		if(this.root!=null){
			this.root.preOrder();
		}else{
			System.out.println("二叉树为空，无法创建！");
		}
	}
　　　　 //中序遍历
	public void infixOrder(){
		if(this.root!=null){
			this.root.infixOrder();
		}else{
			System.out.println("二叉树为空，无法创建！");
		}
	}
　　　　  //后序遍历
	public void postOrder(){
		if(this.root!=null){
			this.root.postOrder();
		}else{
			System.out.println("二叉树为空，无法创建！");
		}
	}
}
//先创建节点
class HeroNode{

	private int no;
	private String name;
	private HeroNode left;   //默认为null
	private HeroNode right;  //默认为null
	
	public HeroNode(int no,String name){
		this.no = no;
		this.name = name;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public String getName() {
		return name;
	}

	public void setName(String name) {
		this.name = name;
	}

	public HeroNode getLeft() {
		return left;
	}

	public void setLeft(HeroNode left) {
		this.left = left;
	}

	public HeroNode getRight() {
		return right;
	}

	public void setRight(HeroNode right) {
		this.right = right;
	}

	@Override    //代表覆盖方法，重载
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + "]";
	}
	//节点的先序遍历，中序遍历，后续遍历必须定义在这里，因为在二叉树执行递归的时候，只能通过这里找到该方法，否则执行不了。
	public void preOrder(){
		System.out.println(this);  //首先，输出父节点
		if(this.getLeft()!=null){  //如果左孩子存在的话，那么递归左子树
			this.getLeft().preOrder();
		}
		if(this.getRight()!=null){  //如果右孩子存在的话，那么递归右子树
			this.getRight().preOrder();
		}
	}
	
	public void infixOrder(){
		if(this.getLeft()!=null){   //如果左孩子存在的话，那么递归左子树
			this.getLeft().infixOrder();
		}
		System.out.println(this);   //输出父节点
		
		if(this.getRight()!=null){  //如果右孩子存在的话，那么递归右子树
			this.getRight().infixOrder();
		}
	}
	public void postOrder(){
		if(this.getLeft()!=null){   //如果左孩子存在的话，那么递归左子树
			this.getLeft().postOrder();
		}
		if(this.getRight()!=null){  //如果右孩子存在的话，那么递归右子树
			this.getRight().postOrder();
		}
		System.out.println(this);   //输出父节点
	}
	
}

上述代码我们最终得到的结果是：

 与我们示意图中的执行过程相同。