目录
前言:以下代码仅供参考,若有错误欢迎指正哦~
1 年龄巧合
小明和他的表弟一起去看电影,有人问他们的年龄。小明说:今年是我们的幸运年啊。我出生年份的四位数字加起来刚好是我的年龄。表弟的也是如此。已知今年是2014年,并且,小明说的年龄指的是周岁。 请推断并填写出小明的出生年份。 这是一个4位整数,请通过浏览器提交答案,不要填写任何多余的内容(比如,他表弟的出生年份,或是他们的年龄等等) 1988
1 public class Main { 2 3 public static void main(String[] args) { 4 for(int i = 1900;i <= 2014;i++) { 5 int a = i / 1000 + i / 100 % 10 + i / 10 % 10 + i % 10; 6 if(a == 2014 - i) 7 System.out.println("i = "+i); 8 } 9 10 } 11 }
2 出栈次序
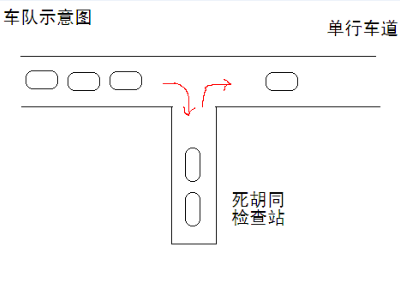
X星球特别讲究秩序,所有道路都是单行线。一个甲壳虫车队,共16辆车,按照编号先后发车,夹在其它车流中,缓缓前行。 路边有个死胡同,只能容一辆车通过,是临时的检查站,如图【p1.png】所示。 X星球太死板,要求每辆路过的车必须进入检查站,也可能不检查就放行,也可能仔细检查。 如果车辆进入检查站和离开的次序可以任意交错。那么,该车队再次上路后,可能的次序有多少种? 为了方便起见,假设检查站可容纳任意数量的汽车。 显然,如果车队只有1辆车,可能次序1种;2辆车可能次序2种;3辆车可能次序5种。 现在足足有16辆车啊,亲!需要你计算出可能次序的数目。 这是一个整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性文字)。 35357670
1 public class Main { 2 public static int count = 1; 3 4 public void dfs(int step, int num, int car) { 5 if(step == num) //当所有排队的汽车均已进栈后 6 return; 7 dfs(step + 1, num, car + 1); 8 if(car > 0) { //当栈不为空时,可以选择出栈 9 count++; 10 dfs(step, num, car - 1); 11 } 12 } 13 14 public static void main(String[] args) { 15 Main test = new Main(); 16 test.dfs(0, 16, 0); 17 System.out.println("DFS: "+count); 18 int r = 1; 19 for(int i = 2;i <= 16;i++) { 20 r = r * (4 * i - 2) / (i + 1); //借鉴网上网友思想:利用卡特兰数 21 } 22 System.out.println(r); 23 } 24 }
3 信号匹配
从X星球接收了一个数字信号序列。 现有一个已知的样板序列。需要在信号序列中查找它首次出现的位置。这类似于串的匹配操作。 如果信号序列较长,样板序列中重复数字较多,就应当注意比较的策略了。可以仿照串的KMP算法,进行无回溯的匹配。这种匹配方法的关键是构造next数组。 next[i] 表示第i项比较失配时,样板序列向右滑动,需要重新比较的项的序号。如果为-1,表示母序列可以进入失配位置的下一个位置进行新的比较。 下面的代码实现了这个功能,请仔细阅读源码,推断划线位置缺失的代码。 // 生成next数组 int* make_next(int pa[], int pn) { int* next = (int*)malloc(sizeof(int)*pn); next[0] = -1; int j = 0; int k = -1; while(j < pn-1){ if(k==-1 || pa[j]==pa[k]){ j++; k++; next[j] = k; } else k = next[k]; } return next; } // da中搜索pa, da的长度为an, pa的长度为pn int find(int da[], int an, int pa[], int pn) { int rst = -1; int* next = make_next(pa, pn); int i=0; // da中的指针 int j=0; // pa中的指针 int n = 0; while(i<an){ n++; if(da[i]==pa[j] || j==-1){ i++; j++; } else __________________________; //填空位置 if(j==pn) { rst = i-pn; break; } } free(next); return rst; } int main() { int da[] = {1,2,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,1,2,1,2,3}; int pa[] = {1,2,1,1,2,1,1,1,2}; int n = find(da, sizeof(da)/sizeof(int), pa, sizeof(pa)/sizeof(int)); printf("%d ", n); return 0; } 注意:通过浏览器提交答案。只填写缺少的内容,不要填写任何多余的内容(例如:说明性文字或已有符号) j = next[j]
4 生物芯片
X博士正在研究一种生物芯片,其逻辑密集度、容量都远远高于普通的半导体芯片。 博士在芯片中设计了 n 个微型光源,每个光源操作一次就会改变其状态,即:点亮转为关闭,或关闭转为点亮。 这些光源的编号从 1 到 n,开始的时候所有光源都是关闭的。 博士计划在芯片上执行如下动作: 所有编号为2的倍数的光源操作一次,也就是把 2 4 6 8 ... 等序号光源打开 所有编号为3的倍数的光源操作一次, 也就是对 3 6 9 ... 等序号光源操作,注意此时6号光源又关闭了。 所有编号为4的倍数的光源操作一次。 ..... 直到编号为 n 的倍数的光源操作一次。 X博士想知道:经过这些操作后,某个区间中的哪些光源是点亮的。 【输入格式】 3个用空格分开的整数:N L R (L<R<N<10^15) N表示光源数,L表示区间的左边界,R表示区间的右边界。 【输出格式】 输出1个整数,表示经过所有操作后,[L,R] 区间中有多少个光源是点亮的。 例如: 输入: 5 2 3 程序应该输出: 2 再例如: 输入: 10 3 6 程序应该输出: 3 资源约定: 峰值内存消耗 < 256M CPU消耗 < 1000ms 请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。 提交时,注意选择所期望的编译器类型。
1 import java.util.Scanner; 2 3 public class Main { 4 5 public long getP(long X) { 6 long count = 1; 7 for(long i = 2;i <= X / 2;i++) { 8 if(X % i == 0) 9 count++; 10 } 11 return count; 12 } 13 14 public void getResult(long N, long L, long R) { 15 long result = 0; 16 for(long i = L;i <= R;i++) { 17 long count = getP(i); 18 if((count&1) == 1) 19 result++; 20 } 21 System.out.println(result); 22 } 23 24 //完全平方数的因子数为奇数个,其中因子包含1 25 public void getResult1(long N, long L, long R) { 26 long result = R - L + 1; 27 long start = (long) Math.sqrt(L); 28 if(start * start < L) 29 start = start + 1; 30 for(;start * start <= R;start++) { 31 if(start * start >= L && start * start <= R) 32 result--; 33 } 34 System.out.println("借鉴网友解法:"+result); 35 } 36 37 public static void main(String[] args) { 38 Main test = new Main(); 39 Scanner in = new Scanner(System.in); 40 long N = in.nextLong(); 41 long L = in.nextLong(); 42 long R = in.nextLong(); 43 test.getResult(N, L, R); 44 test.getResult1(N, L, R); 45 } 46 47 }
5 Log大侠
atm参加了速算训练班,经过刻苦修炼,对以2为底的对数算得飞快,人称Log大侠。 一天,Log大侠的好友 drd 有一些整数序列需要变换,Log大侠正好施展法力... 变换的规则是: 对其某个子序列的每个整数变为: [log_2 (x) + 1] 其中 [] 表示向下取整,就是对每个数字求以2为底的对数,然后取下整。 例如对序列 3 4 2 操作一次后,这个序列会变成 2 3 2。 drd需要知道,每次这样操作后,序列的和是多少。 【输入格式】 第一行两个正整数 n m 。 第二行 n 个数,表示整数序列,都是正数。 接下来 m 行,每行两个数 L R 表示 atm 这次操作的是区间 [L, R],数列序号从1开始。 【输出格式】 输出 m 行,依次表示 atm 每做完一个操作后,整个序列的和。 例如,输入: 3 3 5 6 4 1 2 2 3 1 3 程序应该输出: 10 8 6 【数据范围】 对于 30% 的数据, n, m <= 10^3 对于 100% 的数据, n, m <= 10^5 资源约定: 峰值内存消耗 < 256M CPU消耗 < 1000ms 请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。 提交时,注意选择所期望的编译器类型。
1 import java.util.Scanner; 2 3 public class Main { 4 public static long sum = 0L; 5 public static int[] number; 6 public static long[] result; 7 8 public int getLog2(int X) { 9 int count = 0; 10 while(X >= 2) { 11 X = X / 2; 12 count++; 13 } 14 return count; 15 } 16 17 public void getResult(int L, int R) { 18 for(int i = L;i <= R;i++) { 19 sum = sum - number[i]; 20 number[i] = getLog2(number[i]) + 1; 21 sum = sum + number[i]; 22 } 23 } 24 25 public static void main(String[] args) { 26 Main test = new Main(); 27 Scanner in = new Scanner(System.in); 28 int n = in.nextInt(); 29 int m = in.nextInt(); 30 number = new int[n + 1]; 31 for(int i = 1;i <= n;i++) { 32 number[i] = in.nextInt(); 33 sum = sum + number[i]; 34 } 35 result = new long[m]; 36 for(int i = 0;i < m;i++) { 37 int L = in.nextInt(); 38 int R = in.nextInt(); 39 test.getResult(L, R); 40 result[i] = sum; 41 } 42 for(int i = 0;i < m;i++) 43 System.out.println(result[i]); 44 } 45 }
6 殖民地
带着殖民扩张的野心,Pear和他的星际舰队登上X星球的某平原。为了评估这块土地的潜在价值,Pear把它划分成了M*N格,每个格子上用一个整数(可正可负)表示它的价值。 Pear要做的事很简单——选择一些格子,占领这些土地,通过建立围栏把它们和其它土地隔开。对于M*N的格子,一共有(M+1)*N+M*(N+1)条围栏,即每个格子都有上下左右四个围栏;不在边界上的围栏被相邻的两个格子公用。大概如下图【p1.png】所示。 图中,蓝色的一段是围栏,属于格子1和2;红色的一段是围栏,属于格子3和4。 每个格子有一个可正可负的收益,而建围栏的代价则一定是正的。 你需要选择一些格子,然后选择一些围栏把它们围起来,使得所有选择的格子和所有没被选的格子严格的被隔开。选择的格子可以不连通,也可以有“洞”,即一个连通块中间有一些格子没选。注意,若中间有“洞”,那么根据定义,“洞”和连通块也必须被隔开。 Pear的目标很明确,花最小的代价,获得最大的收益。 【输入数据】 输入第一行两个正整数M N,表示行数和列数。 接下来M行,每行N个整数,构成矩阵A,A[i,j]表示第i行第j列格子的价值。 接下来M+1行,每行N个整数,构成矩阵B,B[i,j]表示第i行第j列上方的围栏建立代价。 特别的,B[M+1,j]表示第M行第j列下方的围栏建立代价。 接下来M行,每行N+1个整数,构成矩阵C,C[i,j]表示第i行第j列左方的围栏建立代价。 特别的,C[i,N+1]表示第i行第N列右方的围栏建立代价。 【输出数据】 一行。只有一个正整数,表示最大收益。 【输入样例1】 3 3 65 -6 -11 15 65 32 -8 5 66 4 1 6 7 3 11 23 21 22 5 25 22 26 1 1 13 16 3 3 4 6 3 1 2 程序应当输出: 123 【输入样例2】 6 6 72 2 -7 1 43 -12 74 74 -14 35 5 3 31 71 -12 70 38 66 40 -6 8 52 3 78 50 11 62 20 -6 61 76 55 67 28 -19 68 25 4 5 8 30 5 9 20 29 20 6 18 3 19 20 11 5 15 10 3 19 23 6 24 27 8 16 10 5 22 28 14 1 5 1 24 2 13 15 17 23 28 24 11 27 16 12 13 27 19 15 21 6 21 11 5 2 3 1 11 10 20 9 8 28 1 21 9 5 7 16 20 26 2 22 5 12 30 27 16 26 9 6 23 程序应当输出 870 【数据范围】 对于20%的数据,M,N<=4 对于50%的数据,M,N<=15 对于100%的数据,M,N<=200 A、B、C数组(所有的涉及到的格子、围栏输入数据)绝对值均不超过1000。根据题意,A数组可正可负,B、C数组均为正整数。 资源约定: 峰值内存消耗 < 256M CPU消耗 < 3000ms 请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。 提交时,注意选择所期望的编译器类型。
PS:此题未写出正确解答,初步一看,使用贪心法求解,但是调试了好久,只能通过题目给定的第一组数据,下面的代码只能通过题目所给的第一组数据,代表楼主自己当时解题的想法,仅仅是记录一下自己的思考的过程,希望能够给其他同学带来启发。
1 import java.util.Scanner; 2 3 public class Main { 4 public static int m, n; 5 public static int[][] A; 6 public static int[][] B; 7 public static int[][] C; 8 public int[][] step = {{0,1},{1,0}}; //分表表示在M*N单元格中向右、向下行走一步 9 public int[][] step1 = {{-1,0},{1,0},{0,-1},{0,1}};//分别表示向上、下、左、右行走一步 10 11 public void init() { 12 A = new int[m][n]; 13 B = new int[m + 1][n]; 14 C = new int[m][n + 1]; 15 } 16 17 public void getResult() { 18 int[][] judge = new int[n][m]; 19 for(int i = 0;i < n;i++) 20 for(int j = 0;j < m;j++) 21 if(A[i][j] < 0) //收益为负数,直接舍弃 22 judge[i][j] = -1; 23 for(int i = 0;i < m;i++) 24 for(int j = 0;j < n;j++) { 25 int v = B[i][j] + B[i + 1][j] + C[i][j] + C[i][j + 1]; 26 A[i][j] = A[i][j] - v; 27 if(A[i][j] >= 0) //减去围栏造价,收益不为负,一定收录 28 judge[i][j] = 1; 29 } 30 for(int i = 0;i < m;i++) //处理相邻围栏重复问题 31 for(int j = 0;j < n;j++) { 32 if(judge[i][j] == -1 || judge[i][j] == 0) 33 continue; 34 for(int k = 0;k < 2;k++) { 35 int x = i + step[k][0]; 36 int y = j + step[k][1]; 37 if(x < m && y < n) { 38 if(judge[x][y] == 1) { 39 if(k == 0) { 40 A[i][j] = A[i][j] + C[x][y]; 41 A[x][y] = A[x][y] + C[x][y]; 42 } 43 else { 44 A[i][j] = A[i][j] + B[x][y]; 45 A[x][y] = A[x][y] + B[x][y]; 46 } 47 } 48 } 49 } 50 } 51 //重新扫描,选取可能符合要求的单元格 52 for(int i = 0;i < m;i++) 53 for(int j = 0;j < n;j++) { 54 if(judge[i][j] != 1) { 55 for(int k = 0;k < 4;k++) { 56 int x = i + step1[k][0]; 57 int y = j + step1[k][1]; 58 if(x < m && y < n && x >= 0 && y >= 0 && judge[x][y] == 1) { 59 if(k == 0) { 60 A[i][j] = A[i][j] + 2 * B[x + 1][y]; 61 } 62 else if(k == 1){ 63 A[i][j] = A[i][j] + 2 * B[x][y]; 64 } else if(k == 2) { 65 A[i][j] = A[i][j] + 2 * C[x][y + 1]; 66 } else { 67 A[i][j] = A[i][j] + 2 * C[x][y]; 68 } 69 } 70 } 71 if(A[i][j] >= 0) 72 judge[i][j] = 1; 73 else { 74 for(int k = 0;k < 4;k++) { 75 int x = i + step1[k][0]; 76 int y = j + step1[k][1]; 77 if(x < m && y < n && x >= 0 && y >= 0 && judge[x][y] == 1) { 78 if(k == 0) { 79 A[i][j] = A[i][j] - 2 * B[x + 1][y]; 80 } 81 else if(k == 1){ 82 A[i][j] = A[i][j] - 2 * B[x][y]; 83 } else if(k == 2) { 84 A[i][j] = A[i][j] - 2 * C[x][y + 1]; 85 } else { 86 A[i][j] = A[i][j] - 2 * C[x][y]; 87 } 88 } 89 } 90 } 91 } 92 } 93 int sum = 0; 94 for(int i = 0;i < m;i++) 95 for(int j = 0;j < n;j++) 96 if(A[i][j] >= 0) 97 sum = sum + A[i][j]; 98 System.out.println(sum); 99 } 100 101 public static void main(String[] args) { 102 Main test = new Main(); 103 Scanner in = new Scanner(System.in); 104 m = in.nextInt(); 105 n = in.nextInt(); 106 test.init(); 107 for(int i = 0;i < m;i++) 108 for(int j = 0;j < n;j++) 109 A[i][j] = in.nextInt(); 110 for(int i = 0;i < m + 1;i++) 111 for(int j = 0;j < n;j++) 112 B[i][j] = in.nextInt(); 113 for(int i = 0;i < m;i++) 114 for(int j = 0;j < n + 1;j++) 115 C[i][j] = in.nextInt(); 116 test.getResult(); 117 } 118 }